三角形の種類を判定しよう!

物理に関する計算問題などで作図を行う場合、三角形の図形が現れることがある。
電験3種のような資格試験の問題では、純数学のように三角形の種類を証明するのではなく、三角形の種類を手早く判定することが重要である。
何故なら、三角形を「直角三角形」「二等辺三角形」「直角二等辺三角形」「正三角形」のいずれかに判定することできれば、それらの定義や性質を利用することできるからである。
ちなみに直角三角形が「特別な直角三角形」であれば、その関係も利用することができる。
この記事の作成には少々手間がかかりました。
手間のかかる記事を作成した理由は、電験3種に関する「講習会」や「過去問の解説(当サイトを含む)」において三角形の種類の判定が「自明」として扱われていることが多いからです。
「知っていることが前提」なので、知らなかったら「おしまい」なのです。
よって、本記事の内容は「全暗記」してください。
関連記事:平行四辺形の仲間を知ろう!
目次
直角三角形
1.直角三角形の定義
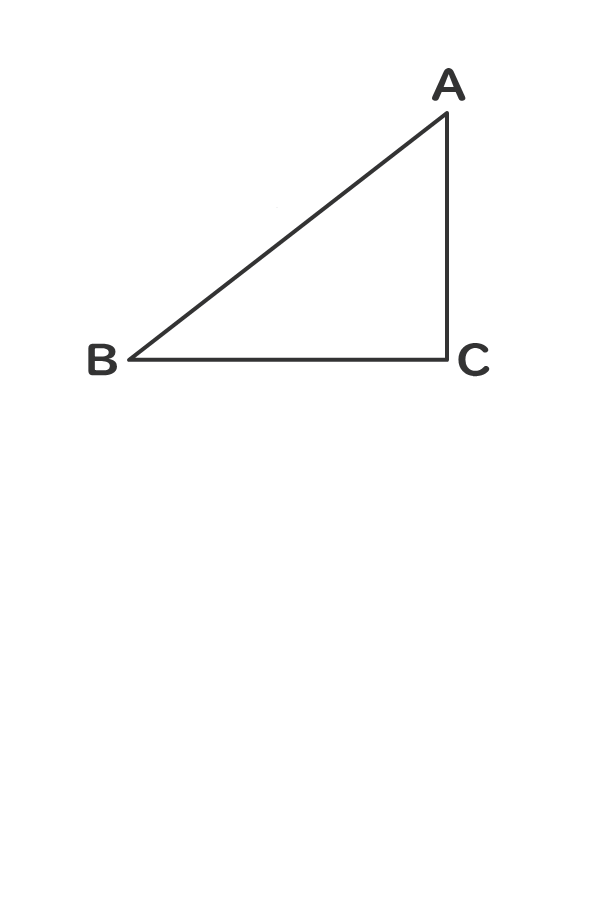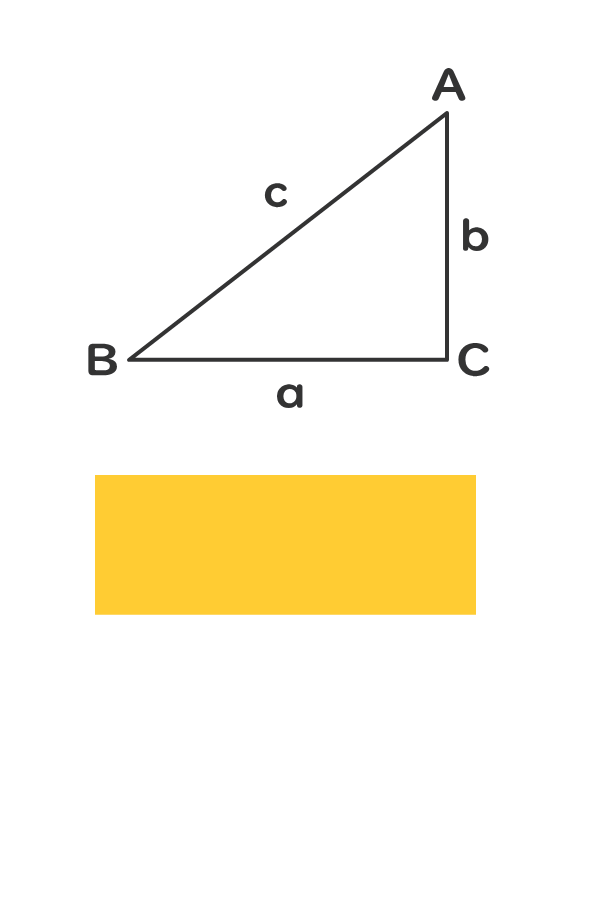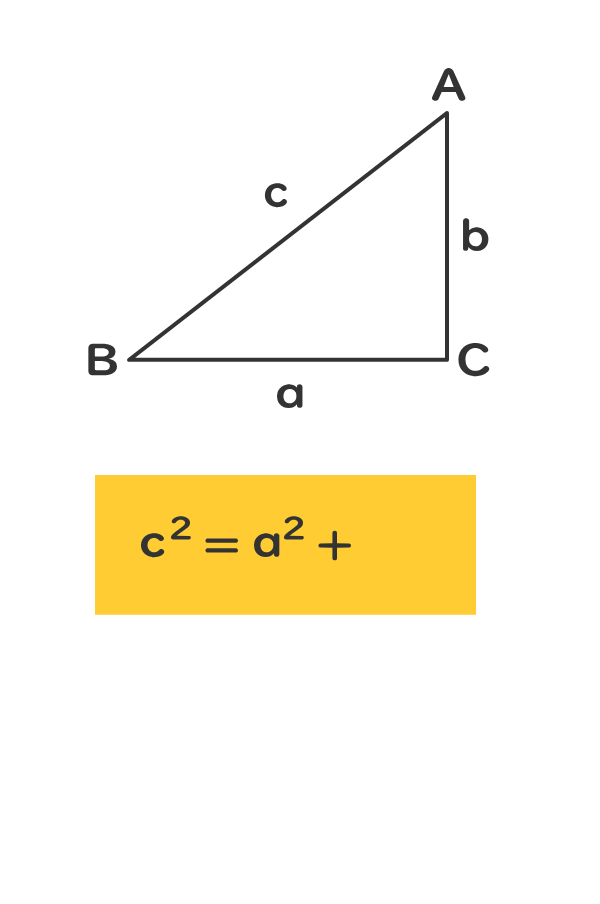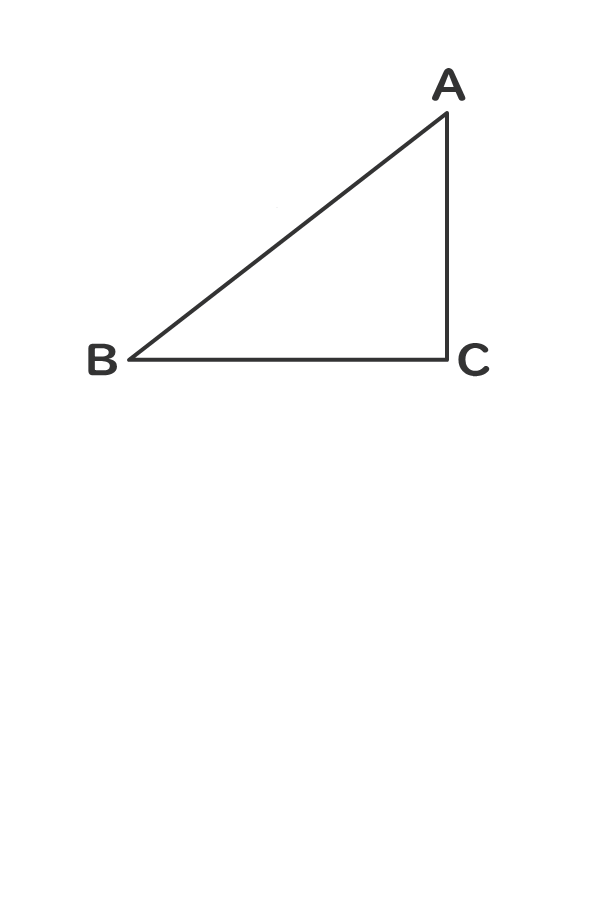
1つの角が直角である三角形を直角三角形という。
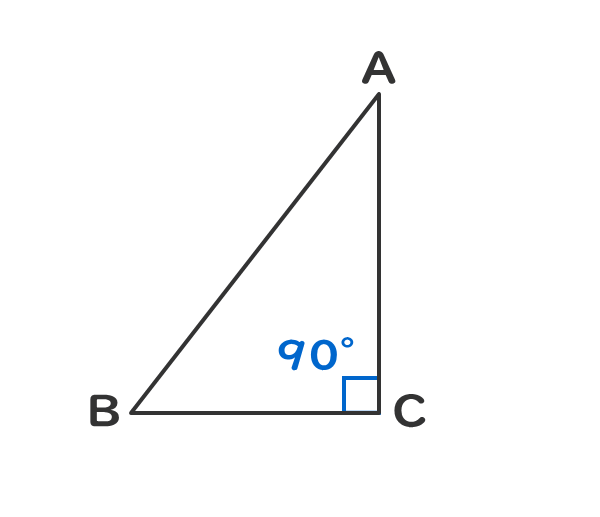
2.直角三角形の性質
直角三角形の3つの辺の長さの関係は、ピタゴラスの定理(三平方の定理)で示すことができる。
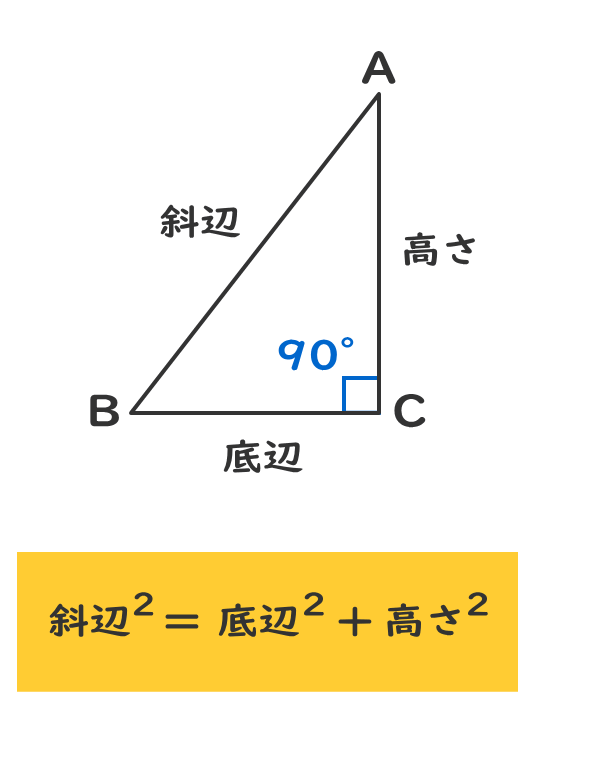
3.直角三角形の判定
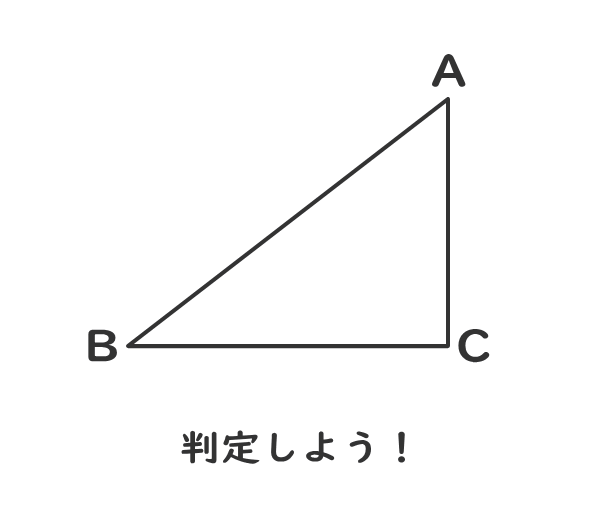
1つの角が直角である。
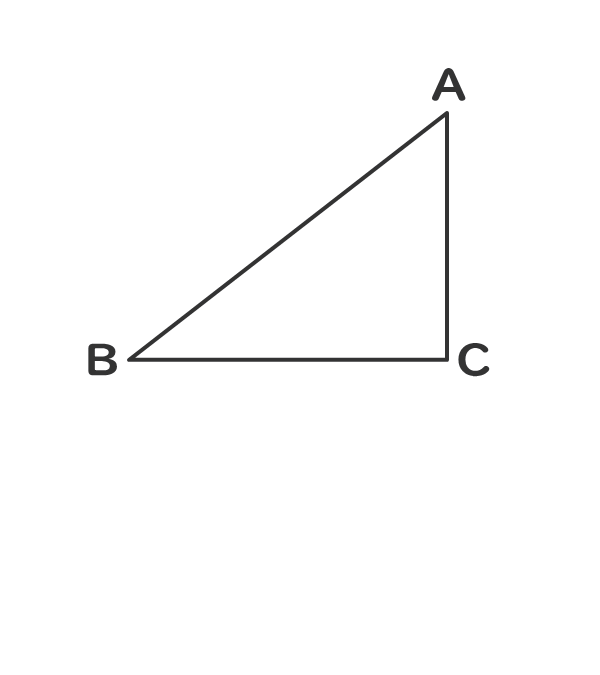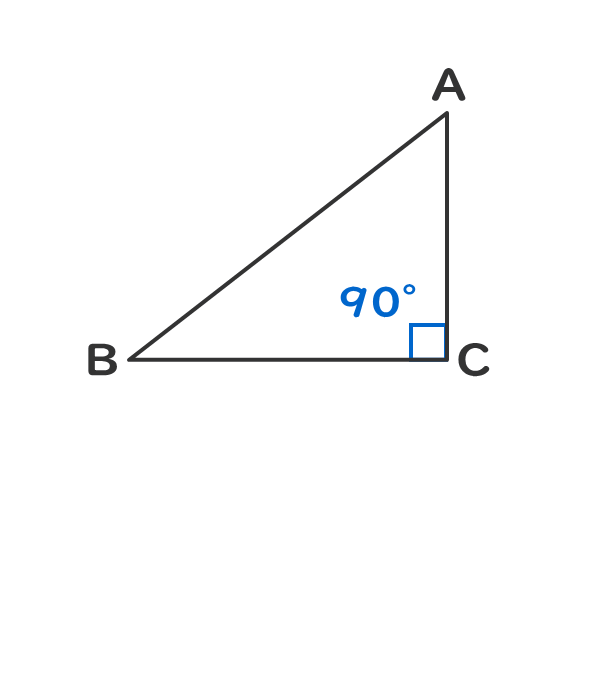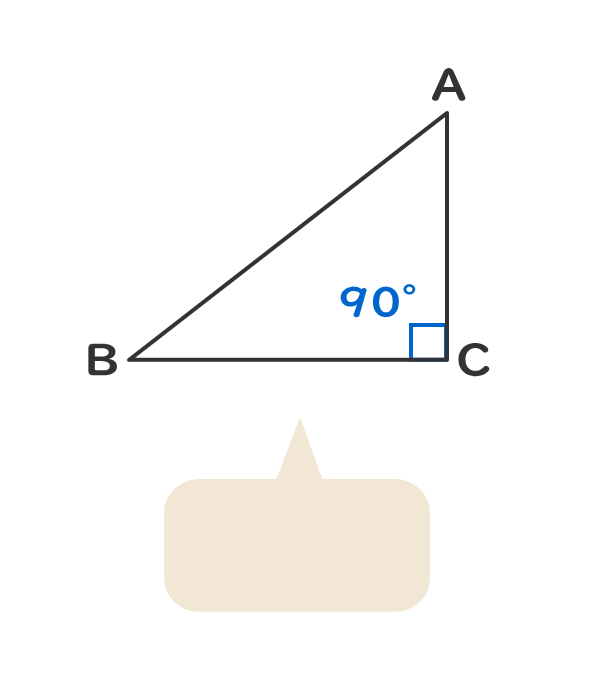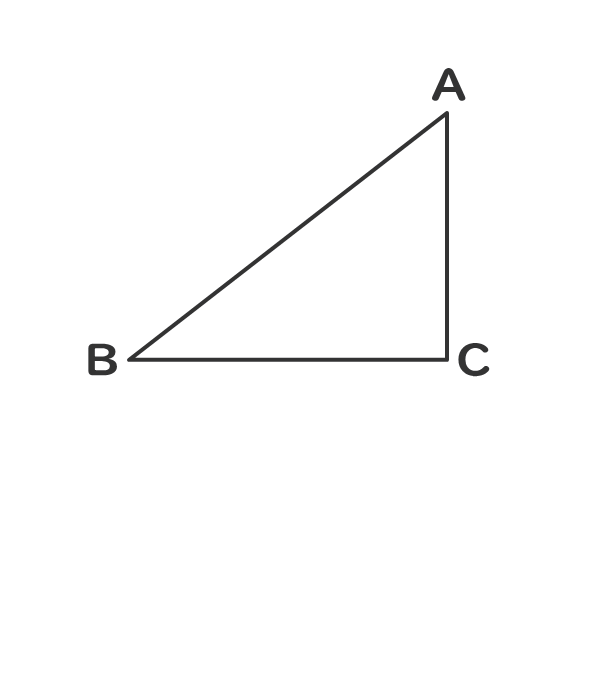
ピタゴラスの定理が成立する。
二等辺三角形
1.二等辺三角形の定義
2つの辺の長さが等しい三角形を二等辺三角形という。
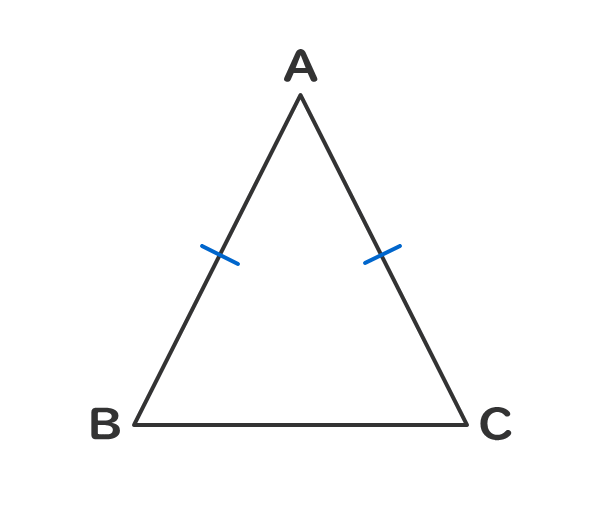
長さが等しい2つの辺の間の角を頂角という。

頂角と向かい合う辺を底辺といい、底辺の両側の角を底角という。
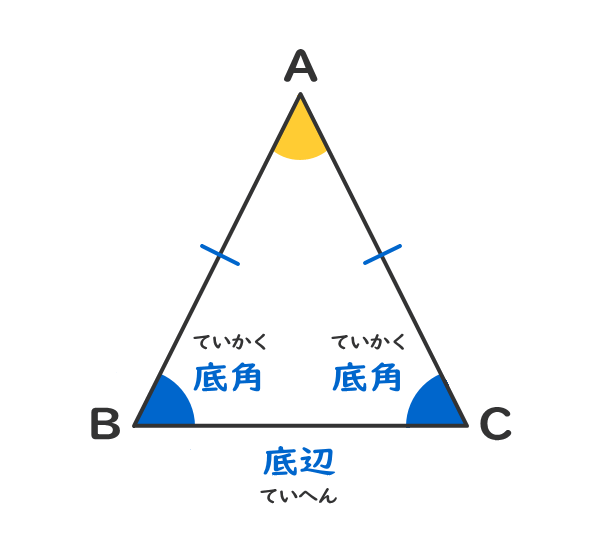
2.二等辺三角形の性質①
二等辺三角形の頂角の二等分線は、底辺を垂直(90°)に二等分する。
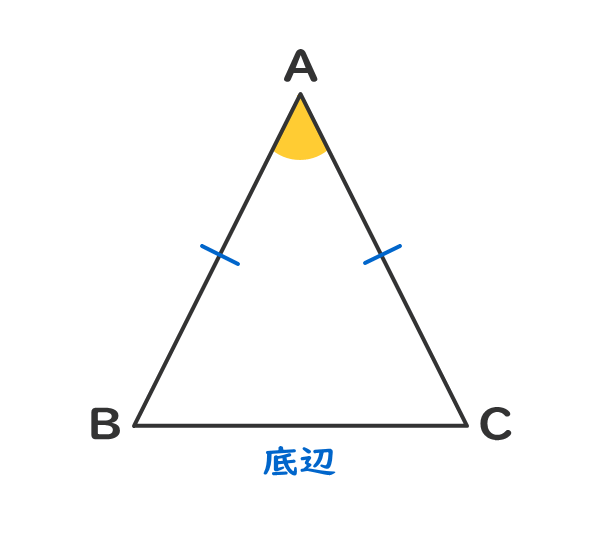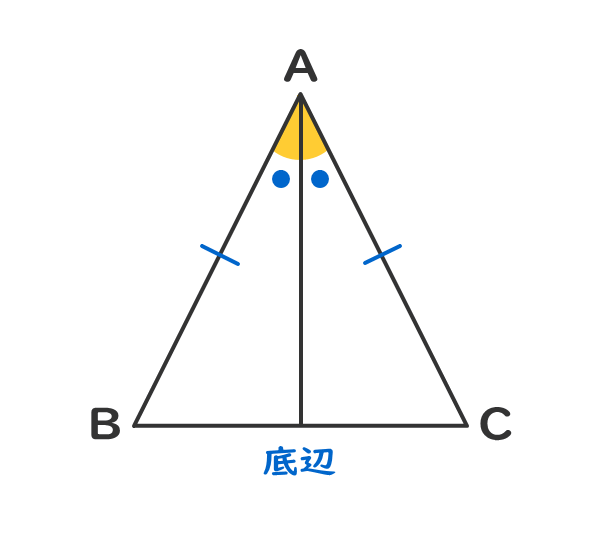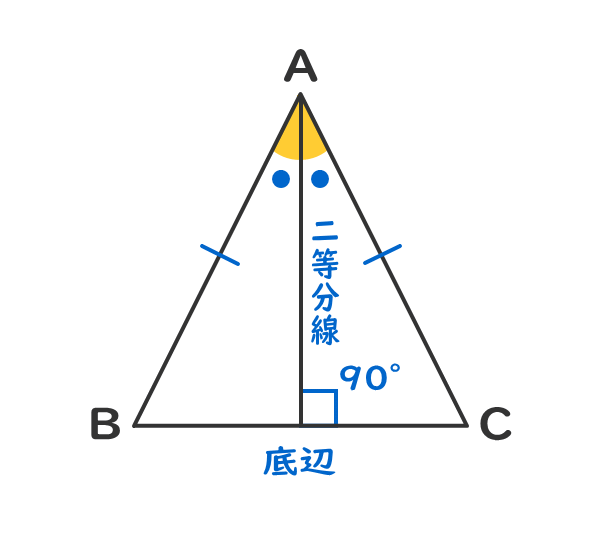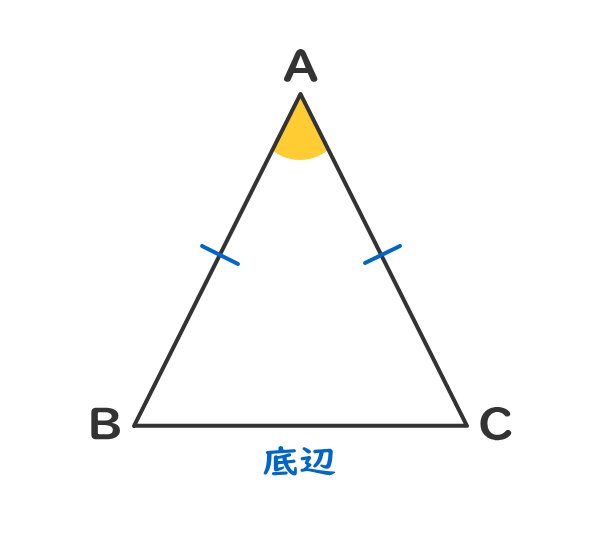
2.二等辺三角形の性質②
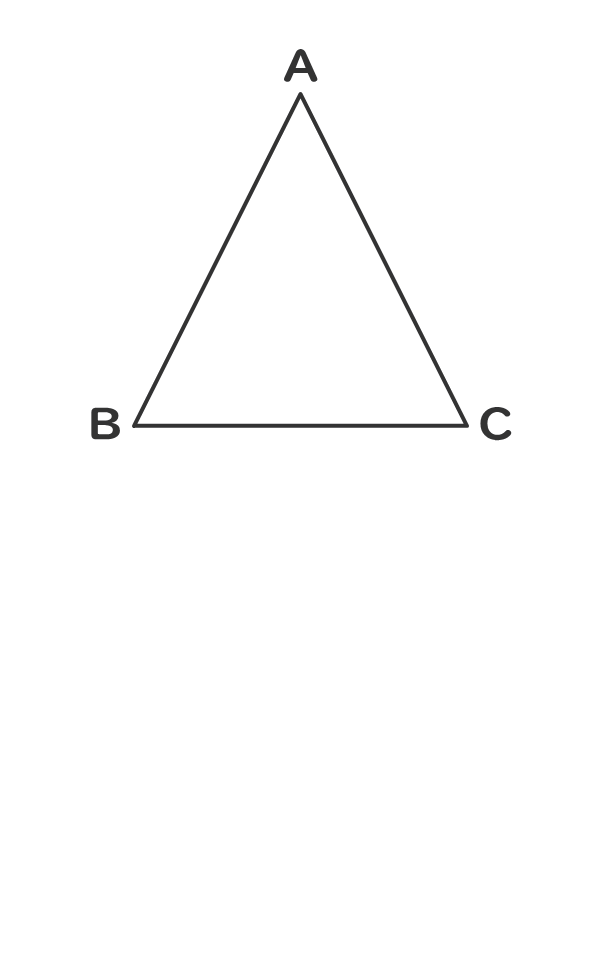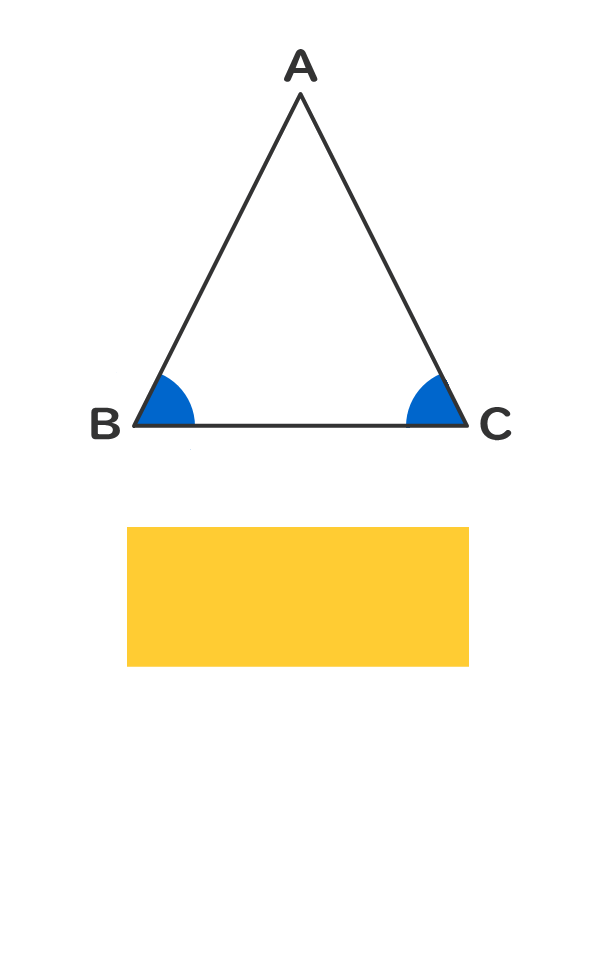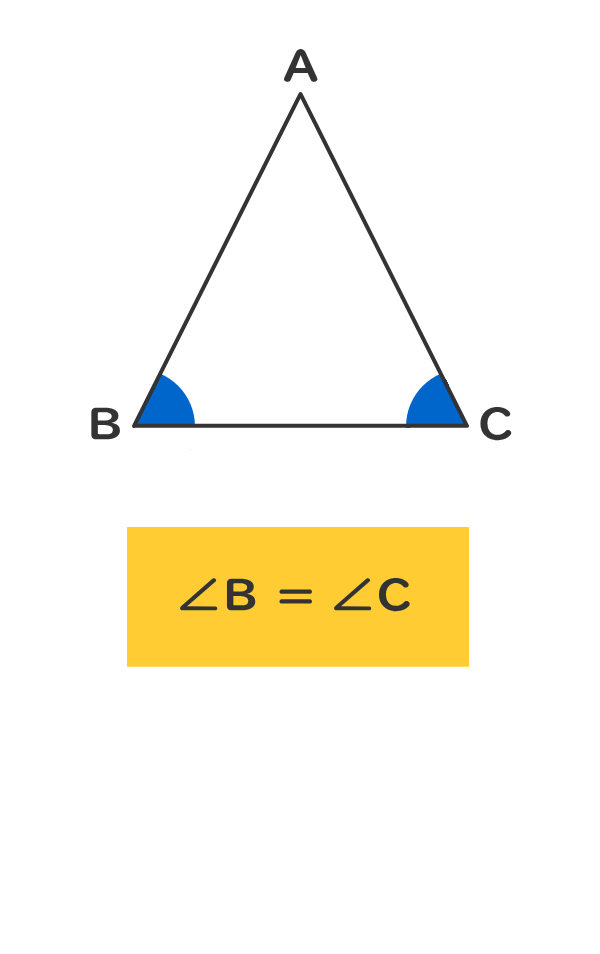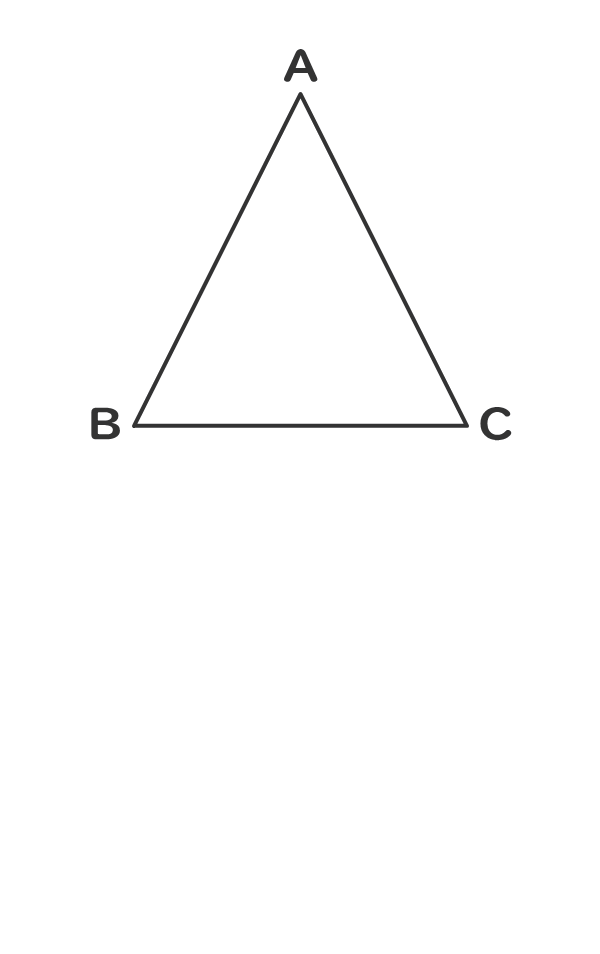
二等辺三角形の底角の角度は等しい。

3.二等辺三角形の判定

2つの辺の長さが等しい。
2つの角の角度が等しい。
4.直角二等辺三角形の判定

2つの辺の長さが等しく、かつ、頂角の角度が90°である。

2つの角の角度が45°である。
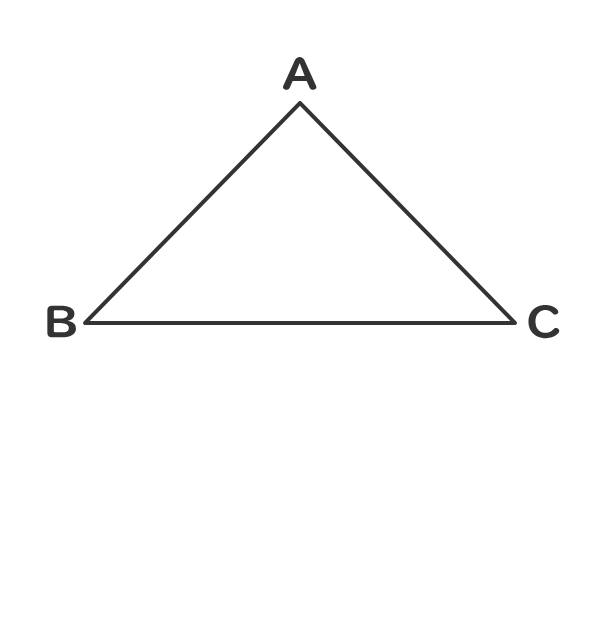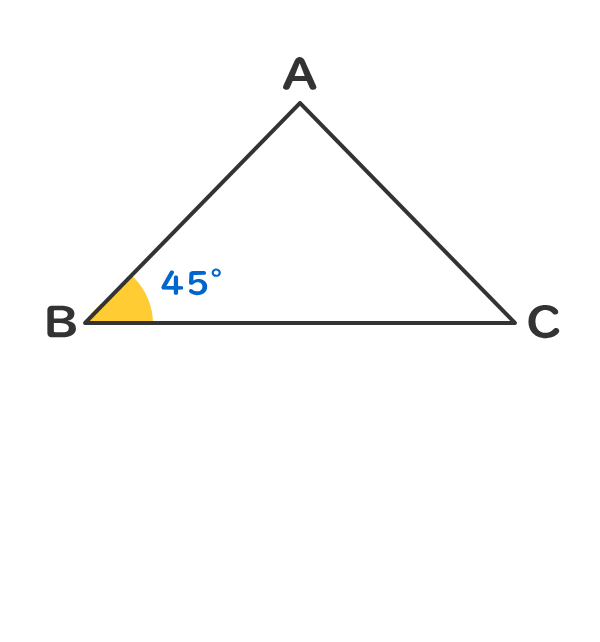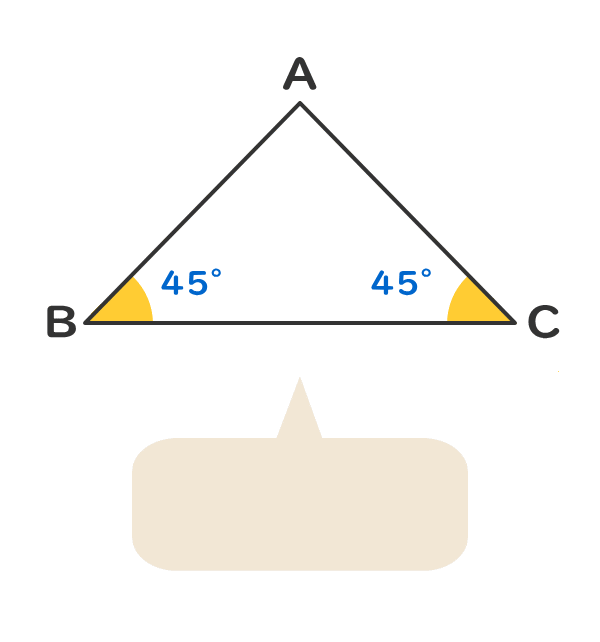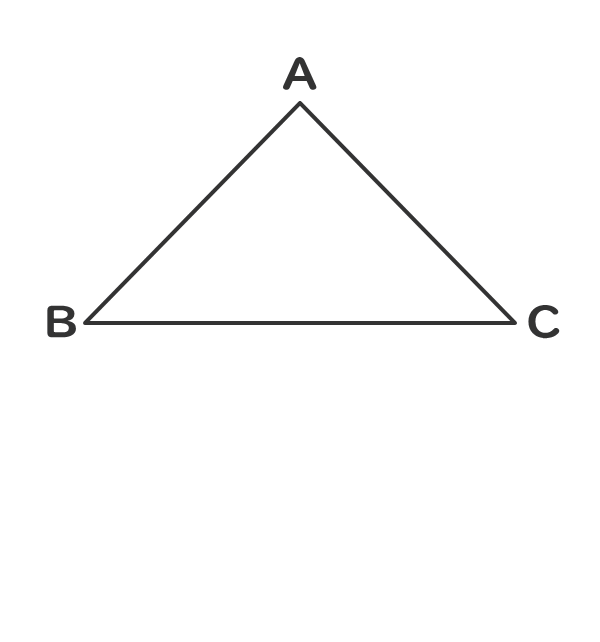
直角二等辺三角形であると判定できた三角形は、直角三角形と二等辺三角形の定義と性質を利用できる。
正三角形
1.正三角形の定義
3つの辺の長さが等しい三角形を正三角形という。
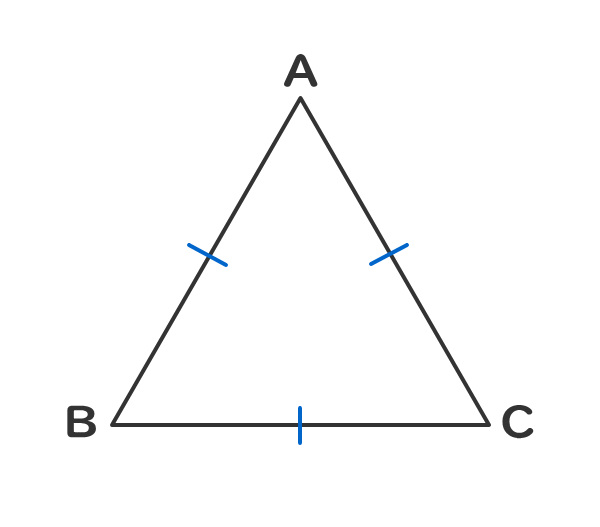
2.正三角形の性質①
3つの角の角度が全て60°である。
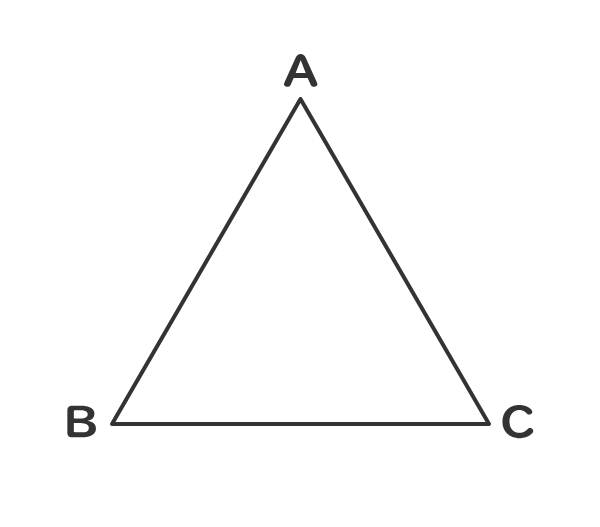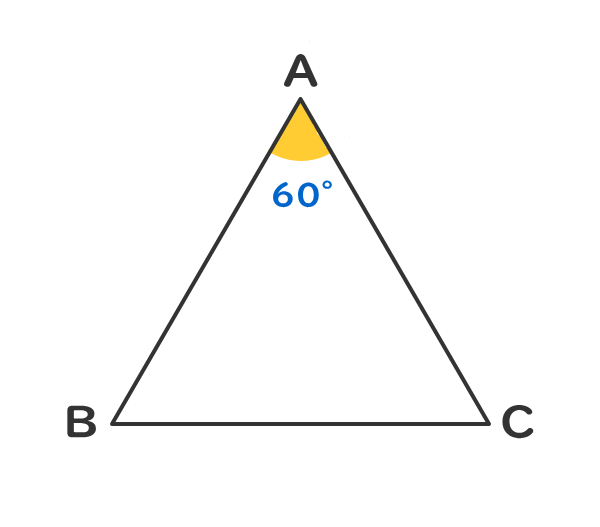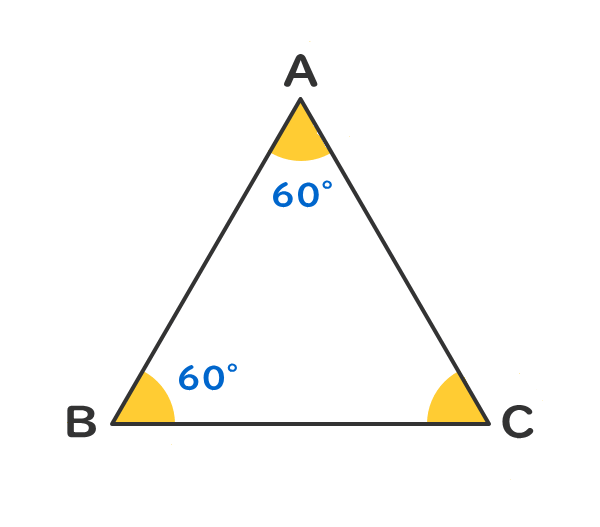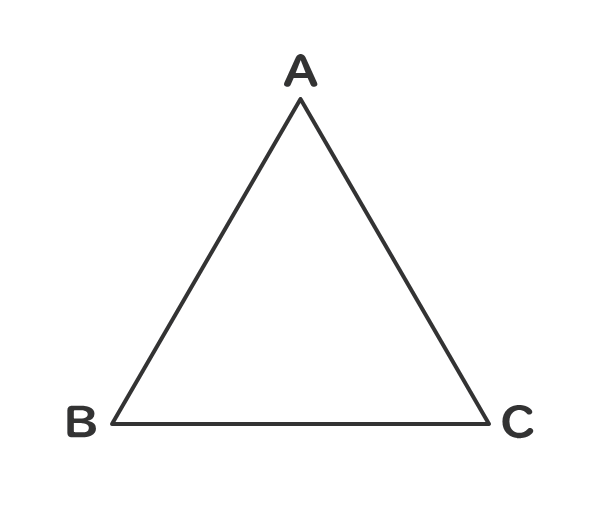
3.正三角形の性質②
二等辺三角形の定義および二等辺三角形の性質①と②を持っている。
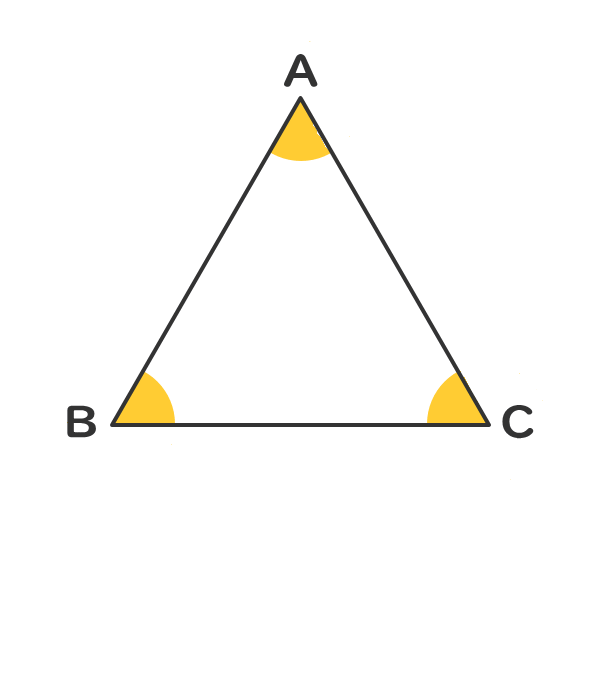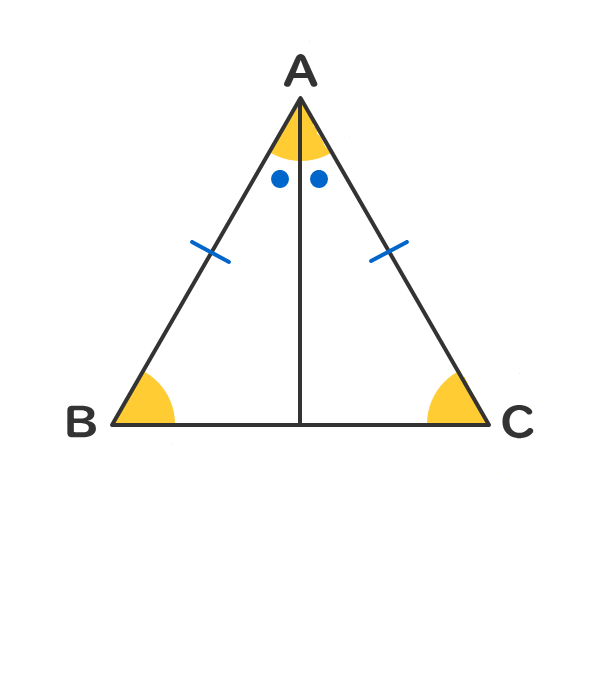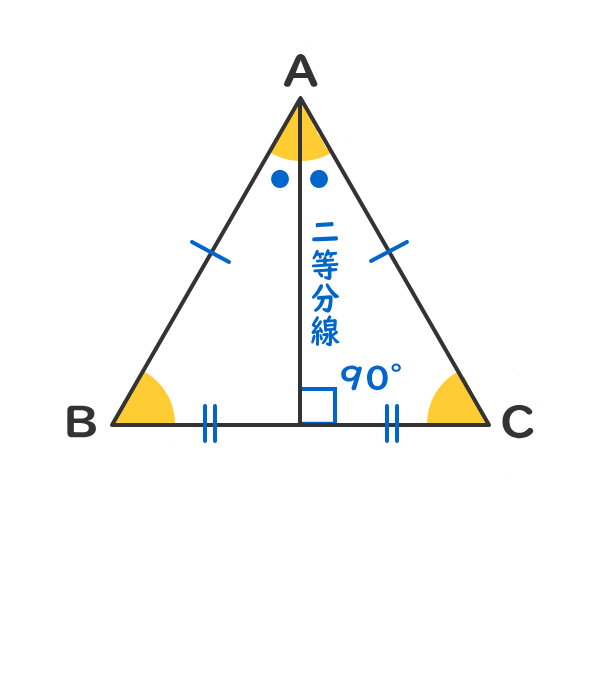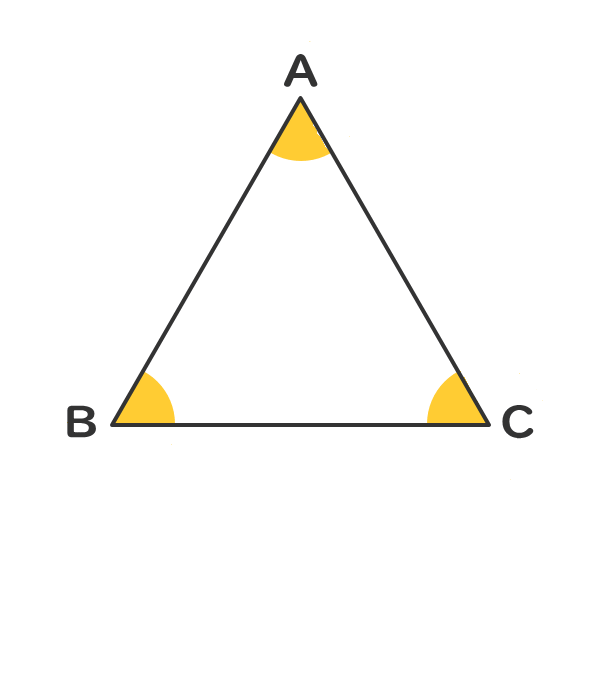
正三角形なので、∠Bまたは∠Cに対して、二等分線を引いても同じ結果になる。
4.正三角形の判定

2つの辺の長さが等しく、かつ、1つの角の角度が60°である。
参考:二等辺三角形の性質「底角は等しい」
参考:三角形の内角の和は180°である。

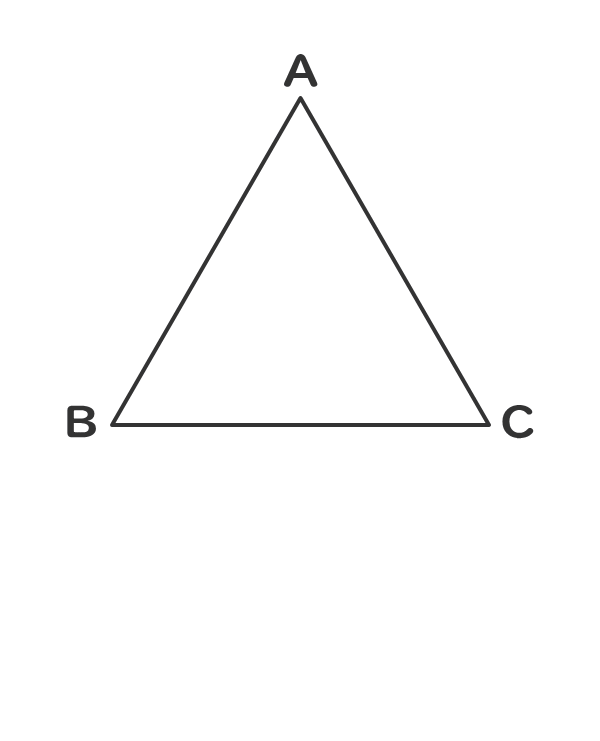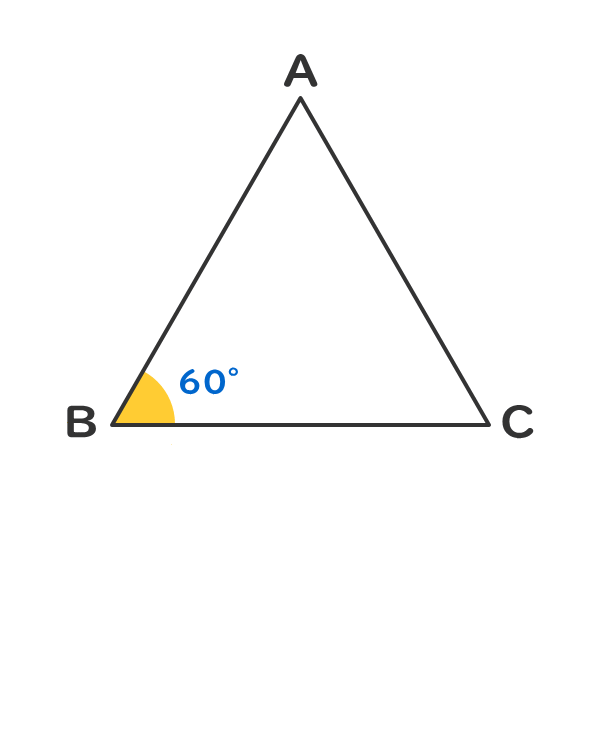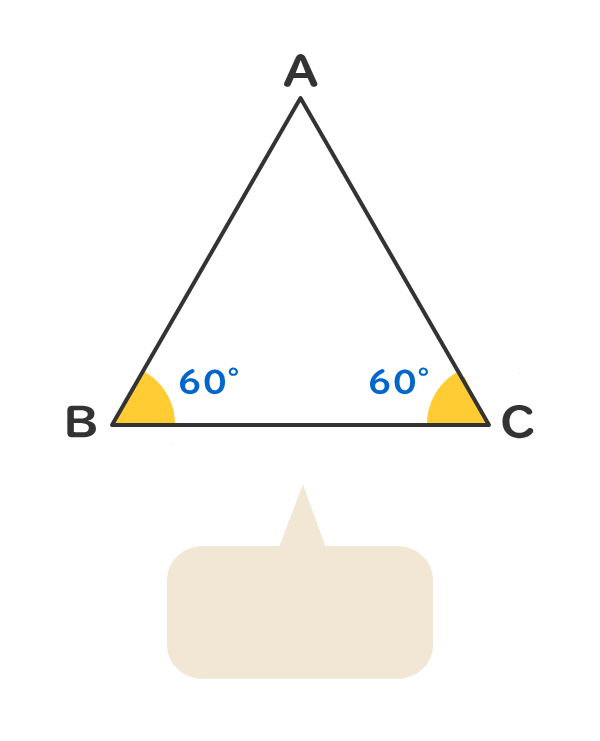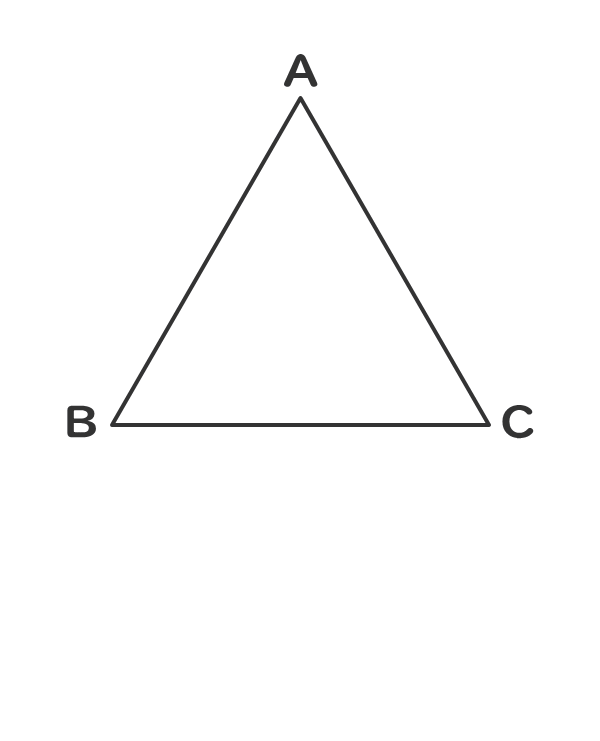
2つの角の角度が60°である。
参考:三角形の内角の和は180°である。