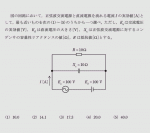
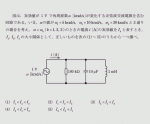
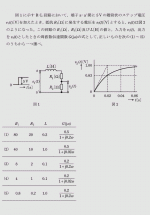
平成30年度機械問1の問題と解答

解答を表示する

解答を非表示にする
平成30年度機械問1の解答ポイント
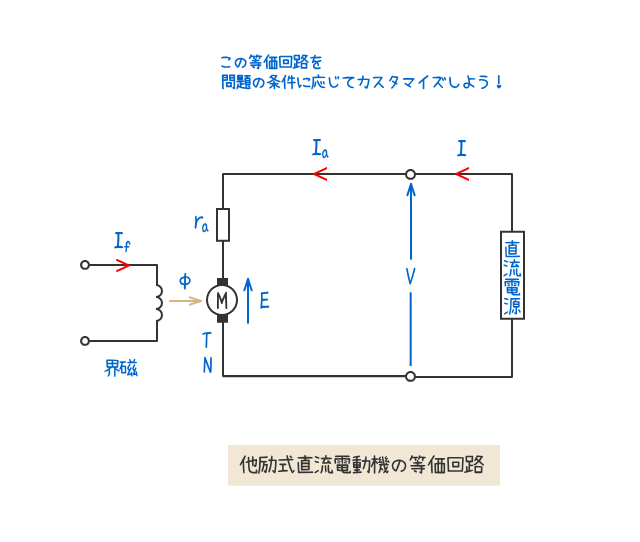
- 本問の「界磁磁束を一定に保った直流電動機」は「他励式直流電動機」の等価回路で考えると分かりやすくなる。
何故なら、「界磁磁束が一定」であるという状況を明確に示すことができるからである。
「分巻式直流電動機」の等価回路で考えても「界磁磁束が一定」であるという状況を示すことは可能であるが、「他励式直流電動機」のほうがより明確である。

- 直流機の誘導起電力E[V]の公式
「直流電動機」と「直流発電機」で適用可能な誘導起電力の公式である。
直流電動機の場合は逆誘導起電力(逆起電力)と呼称する場合がある。
$${E=}{k}{Φ}{N}\quad[V]$$
$$\begin{eqnarray}{E} &:& 直流機の誘導起電力[V]\\\\{k} &:& 比例定数\\\\{Φ} &:& 1極あたりの磁束[Wb]\\\\{N} &:& 回転速度[min^{-1}]\end{eqnarray}$$
$${k}{=}\frac{pz}{60a}$$
$$\begin{eqnarray}{k} &:& 比例定数\\\\{a} &:& 電機子並列回路数\\\\{p} &:& 極数\\\\{z} &:& 電機子全導体数\end{eqnarray}$$
- 直流機のトルクT[N・m]の公式
この公式は「直流電動機」と「直流発電機」で適用可能なトルクの公式である。
$${T=}{k}^{\prime}{Φ}{I_a}\quad[N・m]$$
$$\begin{eqnarray}{T} &:& 直流機のトルク[N・m]\\\\{k}^{\prime} &:& 比例定数\\\\{Φ} &:& 1極あたりの磁束[Wb]\\\\{I_a} &:& 電機子電流[A]\end{eqnarray}$$
$${k}^{\prime}{=}\frac{pz}{2πa}$$
$$\begin{eqnarray}{k}^{\prime} &:& 比例定数\\\\{a} &:& 電機子並列回路数\\\\{p} &:& 極数\\\\{z} &:& 電機子全導体数\end{eqnarray}$$
- 次の①と②の区別が大事
① 未知数と既知数の区別

② 変化する量と変化しない量