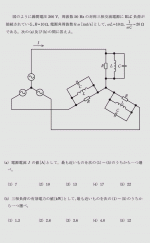
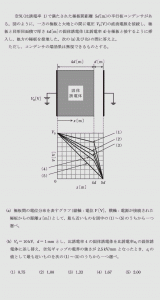
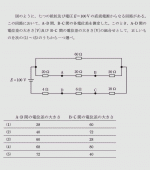
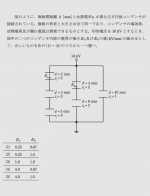
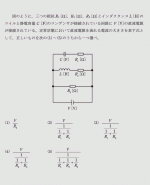
令和元年度理論問9の問題と解答
解答を表示する

解答を非表示にする
令和元年度理論問9の解答ポイント
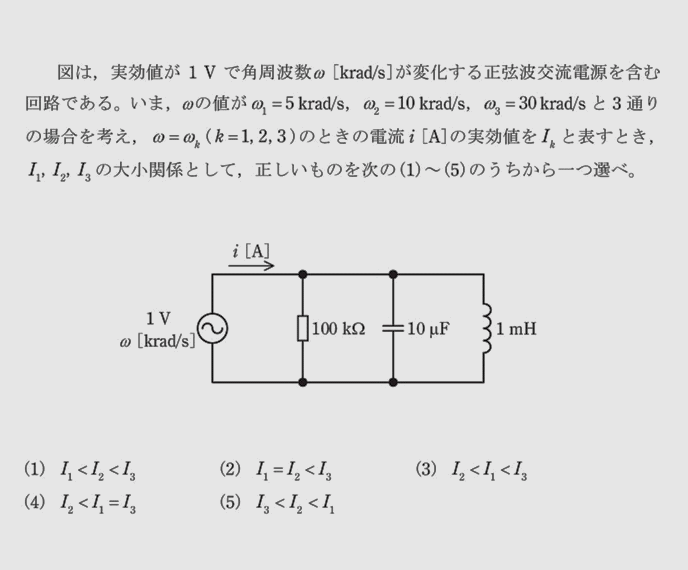
- 本解答は、交流回路計算の基本に従って、電流I1[A]、I2[A]、I3[A]の値を全て計算して、大小関係を明らかにする。
- 参考記事:交流回路の標準計算法「記号法」
- 複素インピーダンスを「いじらない」ことが大事である。
なぜなら「いじると」後の数値計算が面倒になるからである。
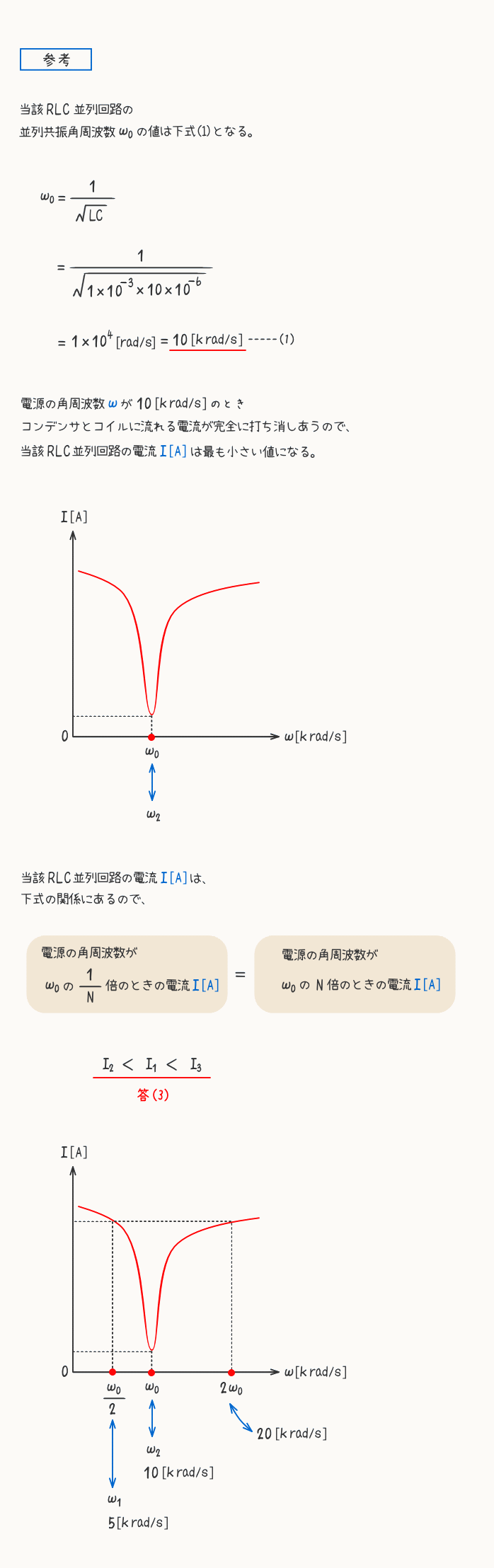
- 本問はRLC並列回路の共振角周波数ω0=10[krad/s]を求めて、(ω2/ω0)=1、(ω1/ω0)=(1/2)、(ω3/ω0)=3の関係から電流I1、I2、I3の大小関係(I2<I1<I3)を明らかにすることができる。
- 前述4が最短の手順であるが、王道の解き方ではないのでおすすめしない。
参考程度にしておこう。
- 並列共振角周波数ω0[rad/s]の公式
$${ω_0=}\frac{1}{\sqrt{LC}}\quad [rad/s]$$
$$\begin{eqnarray}{L} &:& インダクタンス[H]\\\\{C} &:& 静電容量[F]\end{eqnarray}$$
- 並列共振周波数f0[Hz]の公式
$${f_0=}\frac{1}{2π\sqrt{LC}}\quad [Hz]$$
$$\begin{eqnarray}{L} &:& インダクタンス[H]\\\\{C} &:& 静電容量[F]\end{eqnarray}$$
- 参考記事:共振回路と共振周波数および共振角周波数