令和元年度理論問2の問題と解答
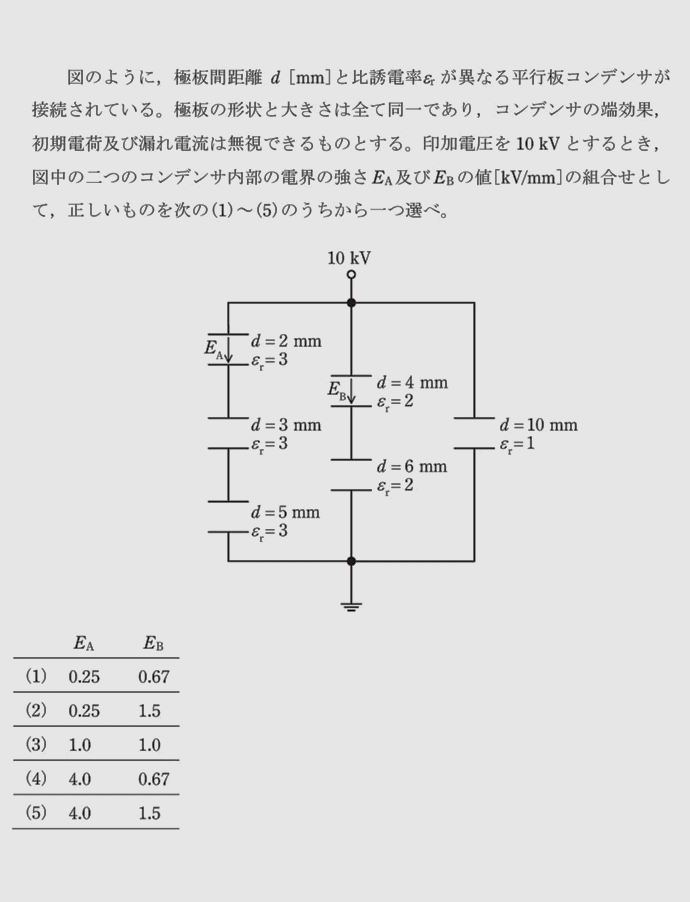
解答を表示する

解答を非表示にする
令和元年度理論問2の解答ポイント
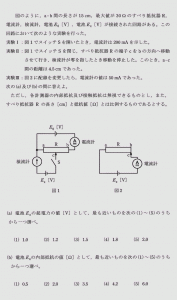
- 本問は「直列接続されたコンデンサの電圧の比例配分式」を利用すれば比較的簡単に正答を導くことができる。
- ただし、初見で最短の解答手順を見せられても「納得」できるとは限らない。
遠回りの手順を知ってこそ「納得」できるという事柄もある。
- 平行板コンデンサの静電容量の公式
$${C=}\frac{ε_0ε_rS}{d}\quad [F]$$
$$\begin{eqnarray}{C} &:& 静電容量[F]\\\\{d} &:& 極板間距離[m]\\\\{ε_0} &:& 真空誘電率[F/m]\\\\{ε_r} &:& 比誘電率\end{eqnarray}$$
- コンデンサの電荷と静電容量と電圧の一般式(コンデンサの形状に無関係に成立するという意味での一般式)
$${Q=CV}\quad [N]$$
$$\begin{eqnarray}{Q} &:& 電荷[C]\\\\{C} &:& 静電容量[F]\\\\{V} &:& 電圧[V]\end{eqnarray}$$
- 平行板コンデンサの電界の強さと電圧の関係
$${E=}\frac{V}{d}\quad [V/m]$$
$$\begin{eqnarray}{E} &:& 電界の強さ[V/m]\\\\{d} &:& 極板間距離[m]\end{eqnarray}$$
- 直列接続されたコンデンサの電圧の比例配分式(ここでは3つの場合を示すが2つでも4つでも同型である)
$${V_1:V_2:V_3=}\frac{1}{C_1}{:}\frac{1}{C_2}{:}\frac{1}{C_3}$$
$$\begin{eqnarray}{V_1,V_2,V_3} &:& 各コンデンサに加わる電圧[V]\\\\{C_1,C_2,C_3} &:& 各コンデンサの静電容量[F]\end{eqnarray}$$
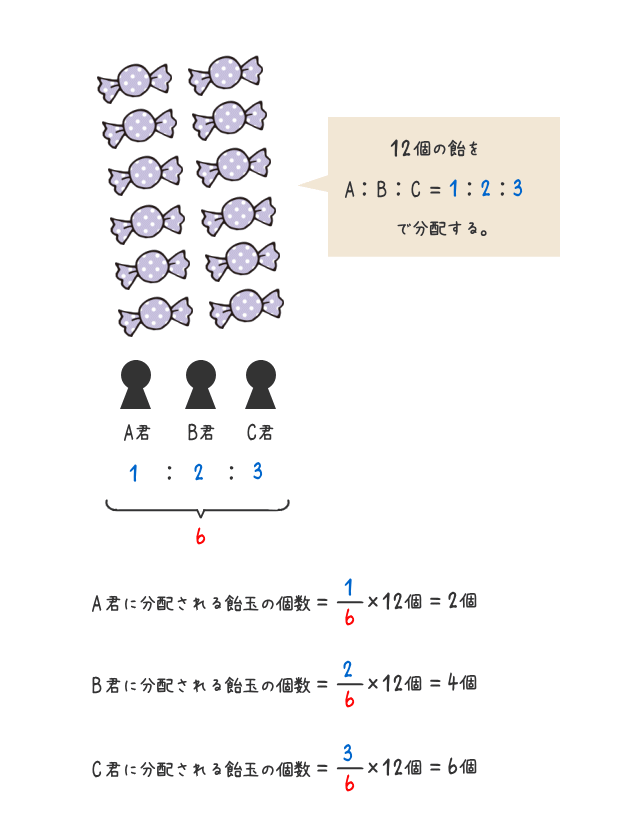
- 六個の飴を三人の子供(A君、B君、C君)に比例分配する例
- 十二個の飴を三人の子供(A君、B君、C君)に比例分配する例