磁気回路
下図のように磁束が通る通路に注目した回路を磁気回路という。

目次
1.磁気回路に関するオームの法則
磁気回路の起磁力をF[A]、通路の磁気抵抗をRm[H-1]、通路を通る磁束をΦ[Wb]とする。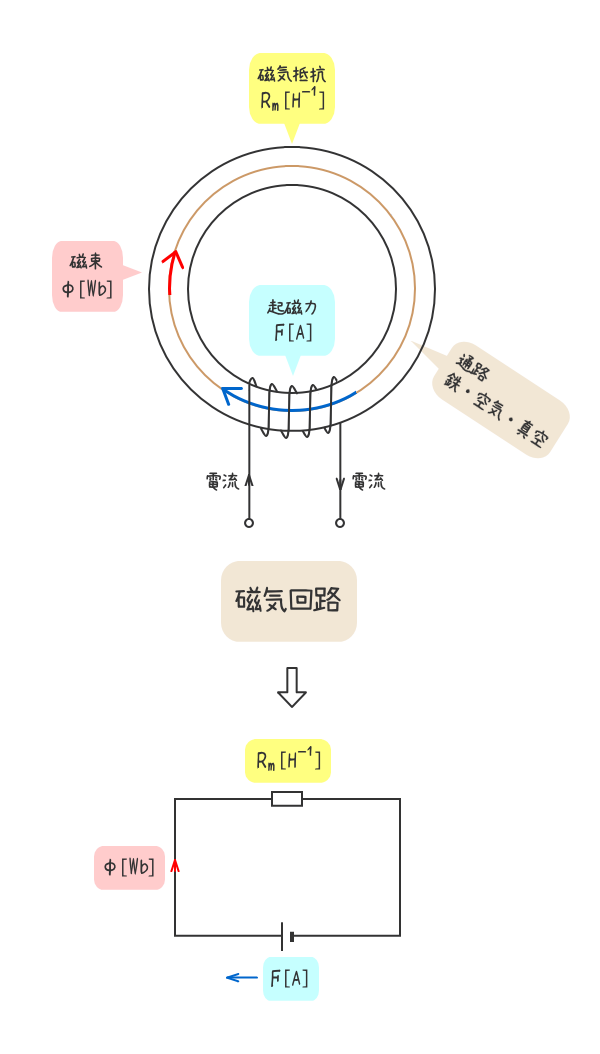
- 磁束は起磁力に比例し、磁気抵抗に反比例する。

- 磁気回路と電気回路の対応
磁気回路 電気回路 ①磁束 ①電流 ②磁気抵抗 ②電気抵抗 ③起磁力 ③起電力(電圧)
2.磁気回路に関するキルヒホッフの法則
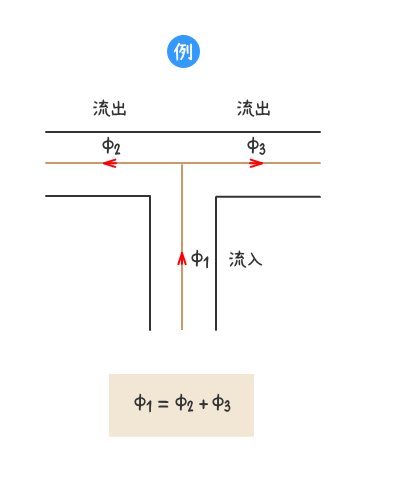
- 磁気回路の結合点に流入する磁束と流出する磁束の総和は等しい。
流入 = 流出

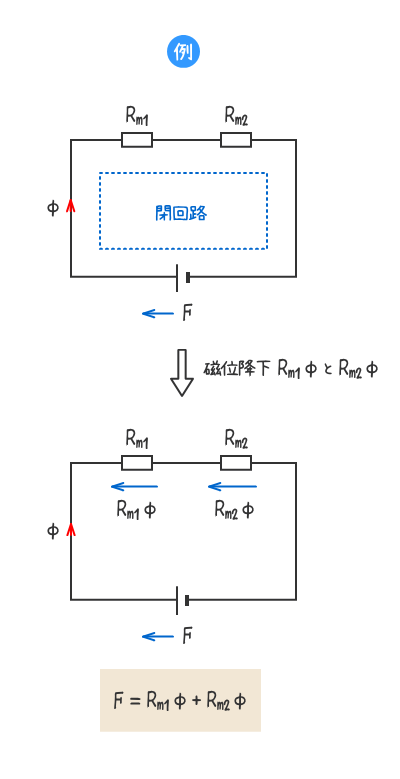
- 磁気回路の閉回路内の起磁力の総和と磁位降下の総和は等しい。
起磁力 = 磁位降下

- 磁気回路と電気回路の対応(追記)
磁気回路 電気回路 ①磁束 ①電流 ②磁気抵抗 ②電気抵抗 ③起磁力 ③起電力(電圧) ④磁位降下 ④電圧降下
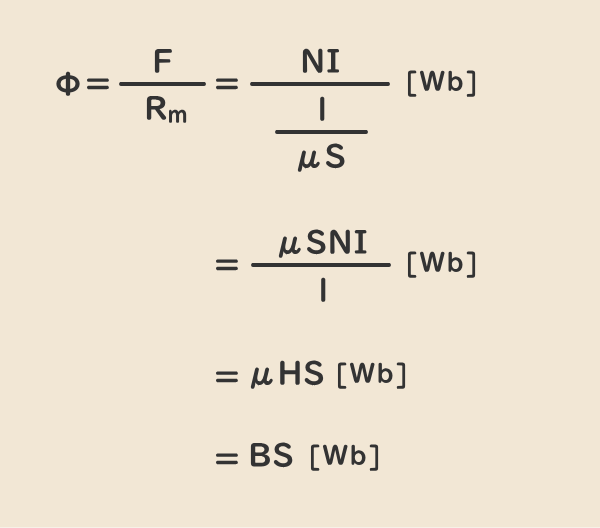
3.磁気回路の関連式
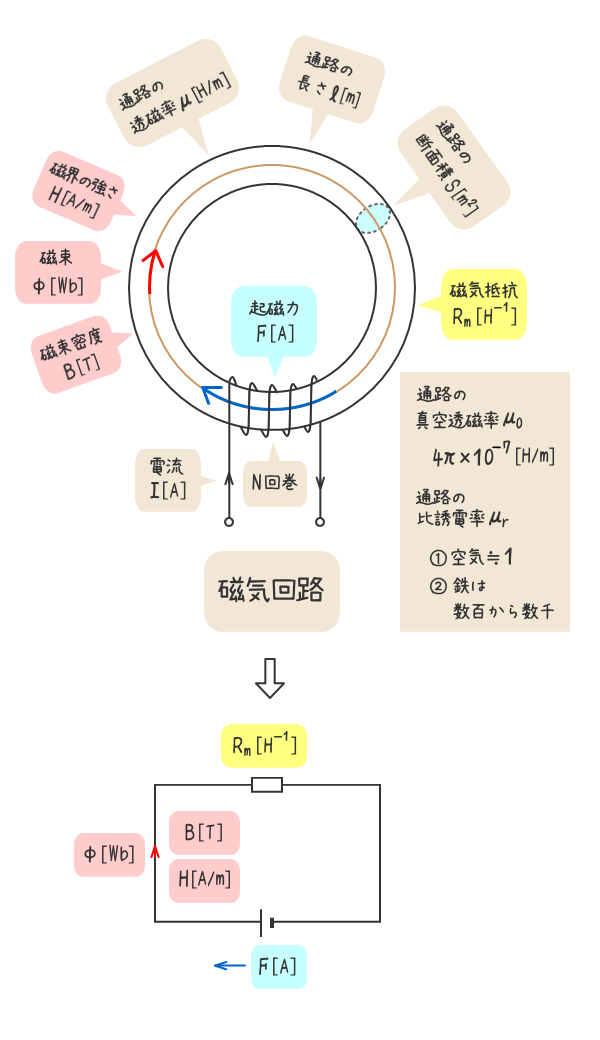
上図の磁気回路に示した諸量で表した式
- 磁束密度B[T]またはB[Wb/m2]

- 透磁率μ[H/m]

- 磁界の強さH[A/m]

- 起磁力F[A]

- 磁気抵抗Rm[H-1]

- 磁束Φ[Wb]

- 磁位降下(Rm×Φ)

- 磁気回路と電気回路の対応(追記)
磁気回路 電気回路 ①磁束 ①電流 ②磁気抵抗 ②電気抵抗 ③起磁力 ③起電力(電圧) ④磁位降下 ④電圧降下 ⑤透磁率 ⑤導電率 ⑥磁界の強さ ⑥電界の強さ ⑦磁束密度 ⑦電流密度
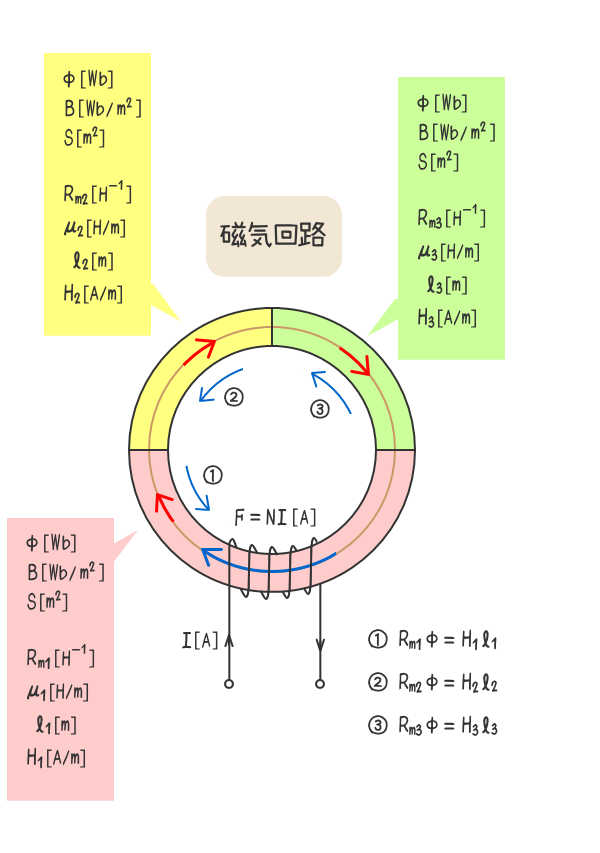
4.複雑な磁気回路に対するキルヒホッフ法則の適用例
下図の磁気回路にキルヒホッフの法則を適用する。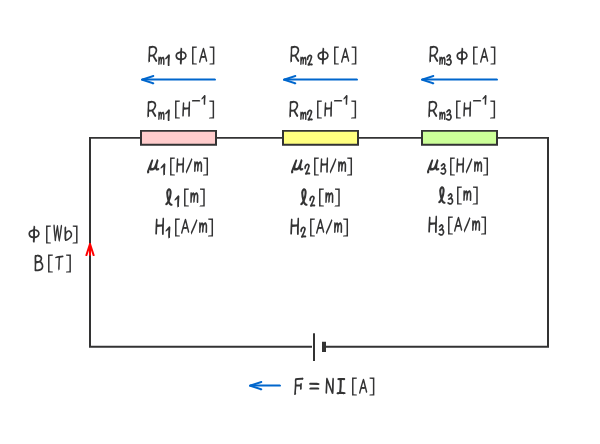
磁気回路の閉回路内の起磁力の総和と磁位降下の総和は等しい。
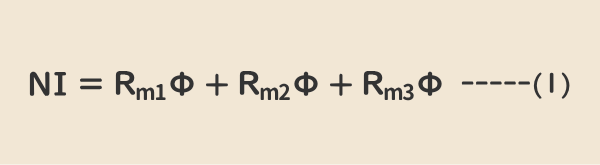
上式(1)は下式(2)で表すことができる。(2.磁気回路の関係式7の磁位降下を参照)
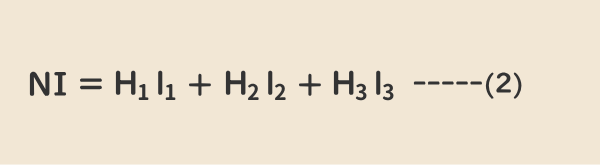
上式(2)はアンペア周回積分の法則を適用した結果と同じである。
上図の磁気回路の参考図を示しておく。
上図の磁気回路中の磁束Φ[Wb]と磁束密度B[T](Wb/m2)が同じなので、磁気回路の通路の断面積S[m2]も同じなるはずである。
逆にいえば、通路の断面積S[m2]が同じ磁気回路に同じ磁束がΦ[Wb]が流れていれば、磁束密度B[T](Wb/m2)も同じになるということである。
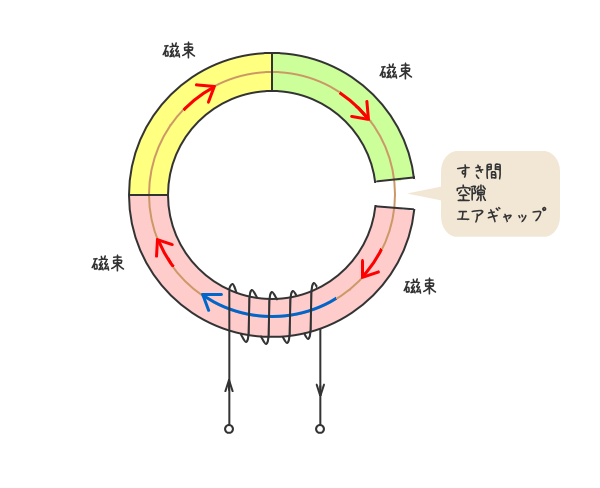
5.磁束は「真空中」でも「空気中」でも容易に流れていくので、通路にすき間があっても構わない。
電気回路は電線がつながっていなければ基本的に電流は流れない。
磁束は電流とは異なり「真空中」でも「空気中」でも容易に流れていく。
ゆえに、磁気回路中にすき間があっても磁束が通る通路として成立する。
ただし、すき間が広すぎると磁束が漏れやすくなる。
鉄は空気よりもさらに磁束が流れやすい。
空気の比透磁率が1なのに対し、鉄は数百~数千である。
空隙の長さが短くても比透磁率が1なので、見た目以上に磁気抵抗は大きくなる。
鉄は長さが長くても比透磁率が数百~数千なので、見た目ほど磁気抵抗は大きくならない。

6.単位の読みかた
- 単位[A]は、「アンペア」と読む。
- 単位[Wb]は、「ウェーバ」と読む。
- 単位[H-1]は、「毎ヘンリー」と読む。
- 単位[T]は、「テスラ」と読む。
- 単位[A/m]は、「アンペア毎メートル」と読む。
- 単位[H/m]は、「ヘンリー毎メートル」と読む。