共振回路と共振周波数および共振角周波数
電気回路の「共振」とは、ある特定の周波数「共振周波数」あるいは「共振角周波数」において、電気回路が「特別な状態」になることをいう。
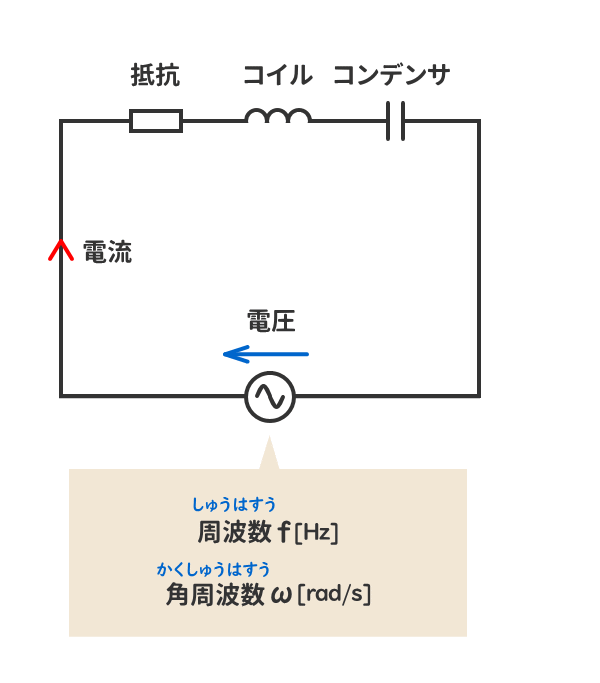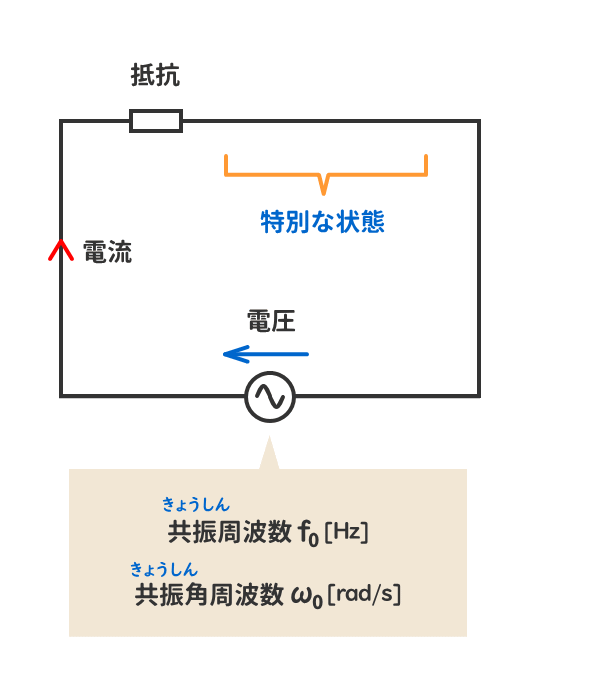
電気回路の「共振」を利用した回路は、無線機器の同調回路として広く用いられている。

目次
1.交流回路の「リアクタンス」の基礎知識
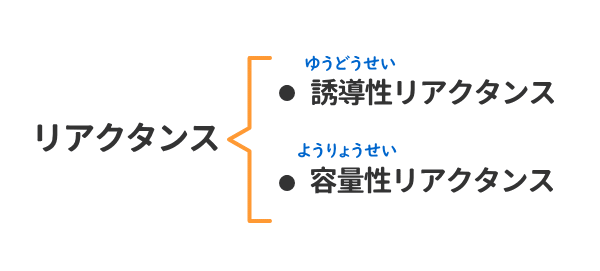
リアクタンスとは、電気回路の「誘導性リアクタンス」と「容量性リアクタンス」の総称である。
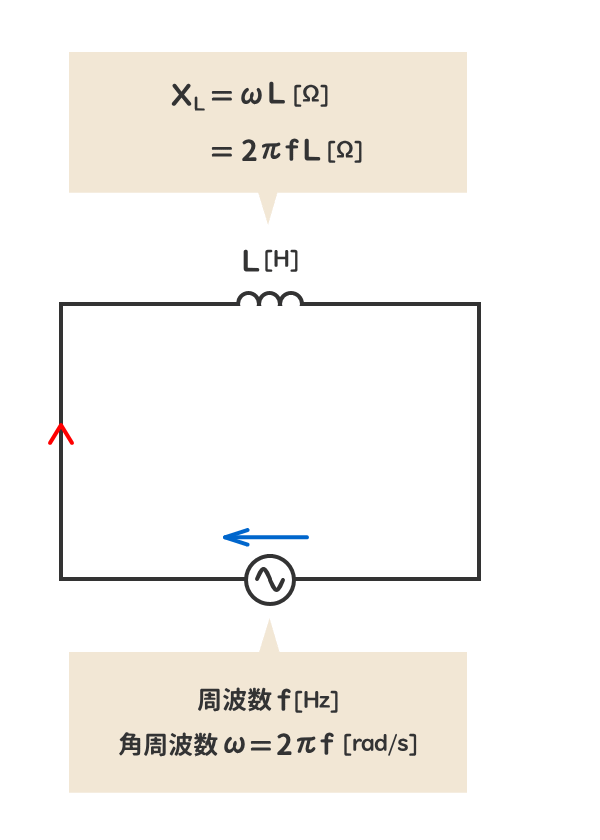
① コイルのインダクタンス[H]をオーム値[Ω]で表した量が「誘導性リアクタンス」である。
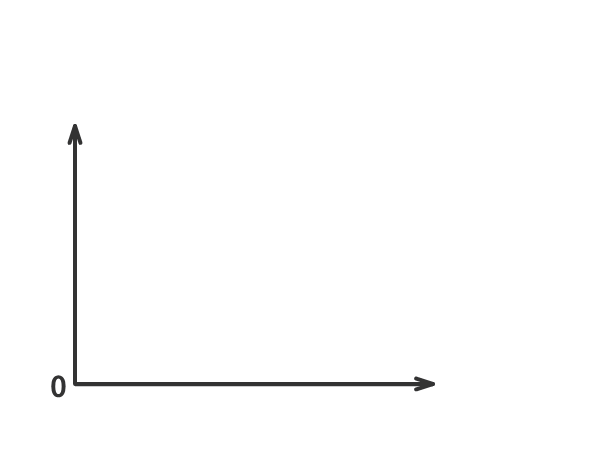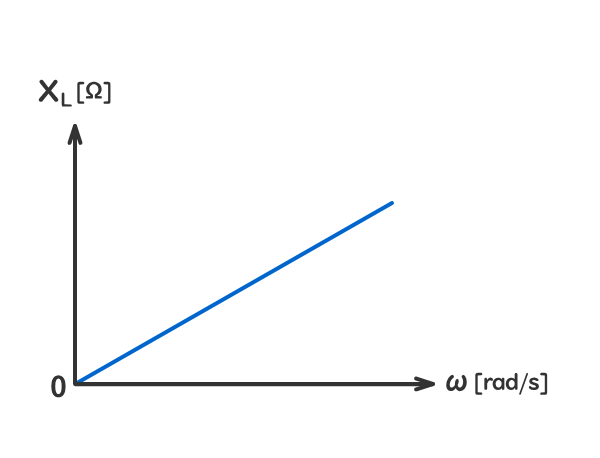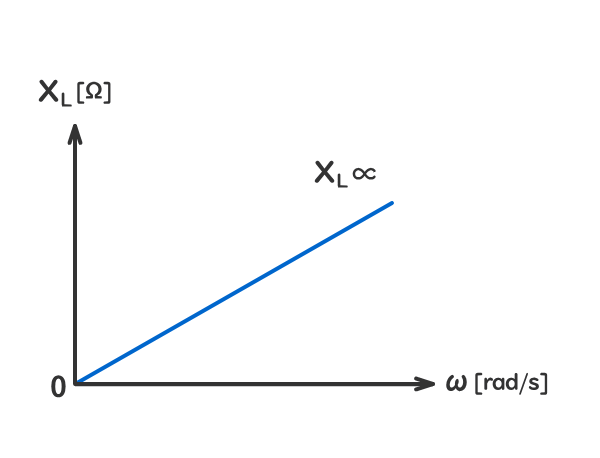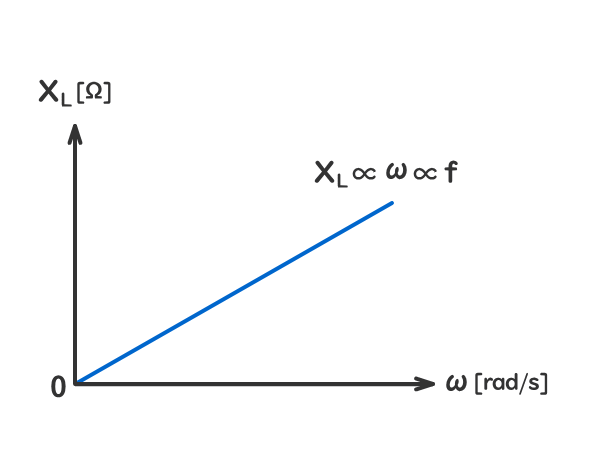
誘導性リアクタンスXL[Ω]は、回路の角周波数ω[rad/s]に比例する。
角周波数ω[rad/s]は、周波数f[H]に比例する。
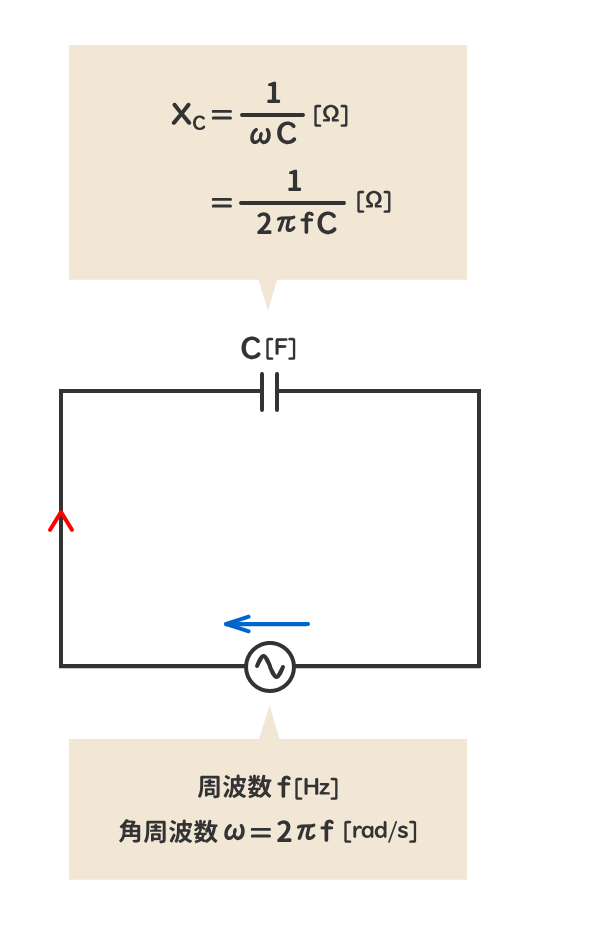
② コンデンサの静電容量[F]をオーム値[Ω]で表した量が「容量性リアクタンス」である。
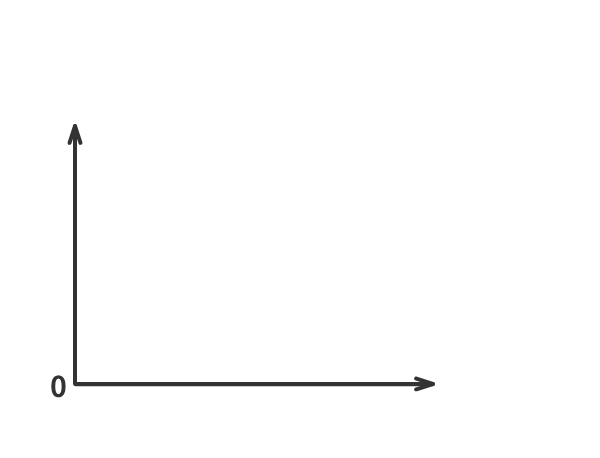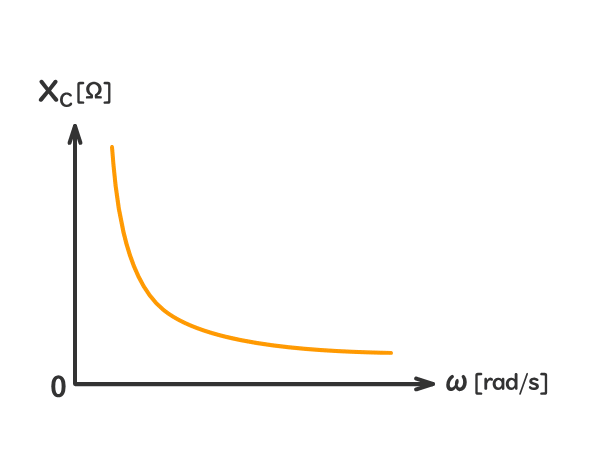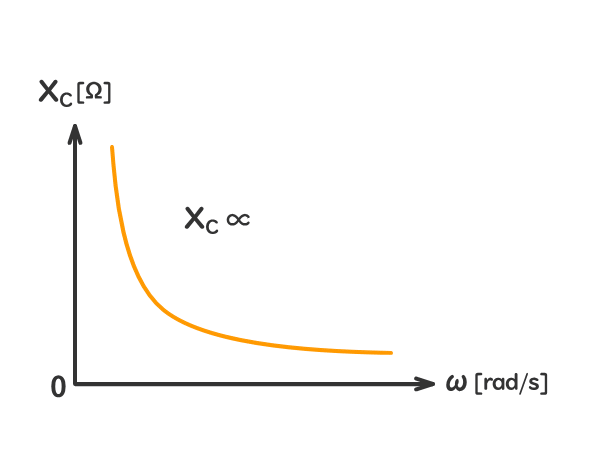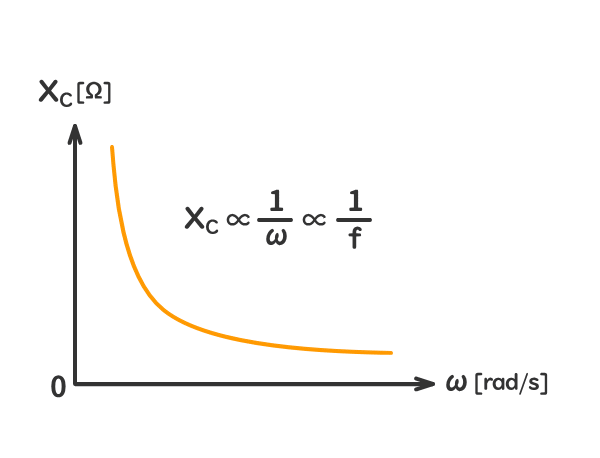
容量性リアクタンスXC[Ω]は、回路の角周波数ω[rad/s]に反比例する。
角周波数ω[rad/s]は、周波数f[H]に比例する。
2.RLC直列交流回路の「特別な状態」とは
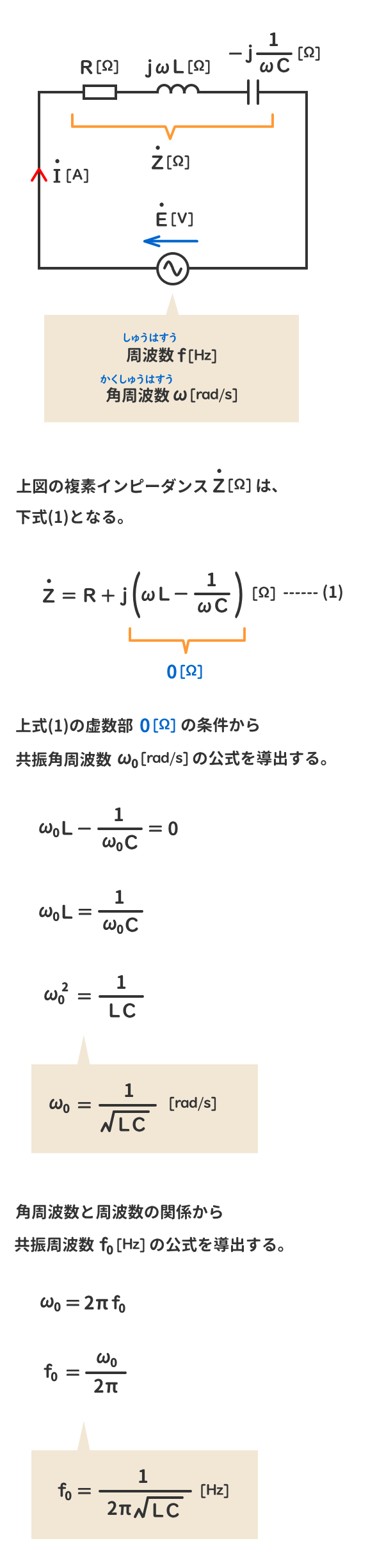
RLC直列交流回路の「特別な状態」とは、複素インピーダンスの虚数部が0[Ω]となる状態をいう。
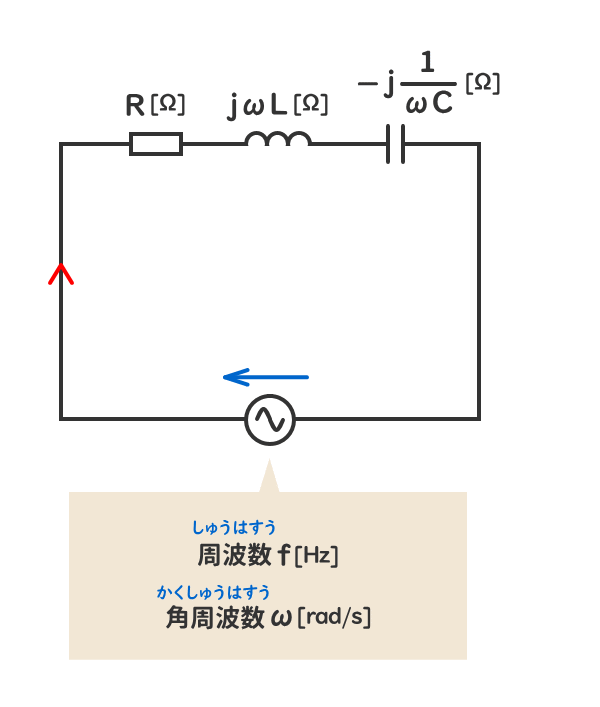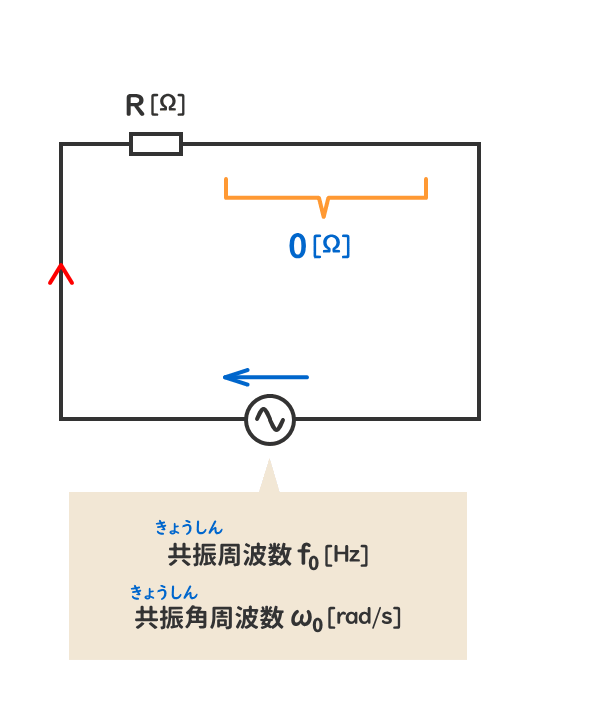
このときの回路の周波数を共振周波数f0[Hz]、角周波数を共振角周波数ω0[rad/s]という。
3.RLC並列交流回路の「特別な状態」とは
RLC並列交流回路の「特別な状態」とは、複素アドミタンスの虚数部が0[S]となる状態をいう。
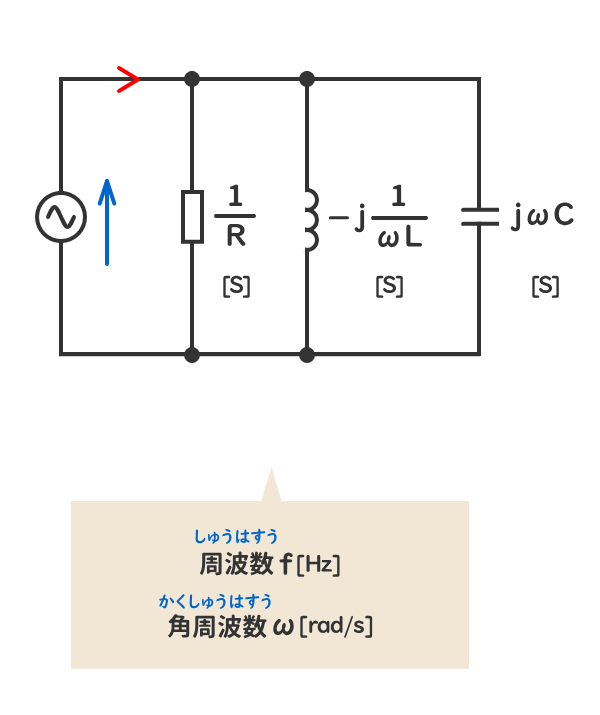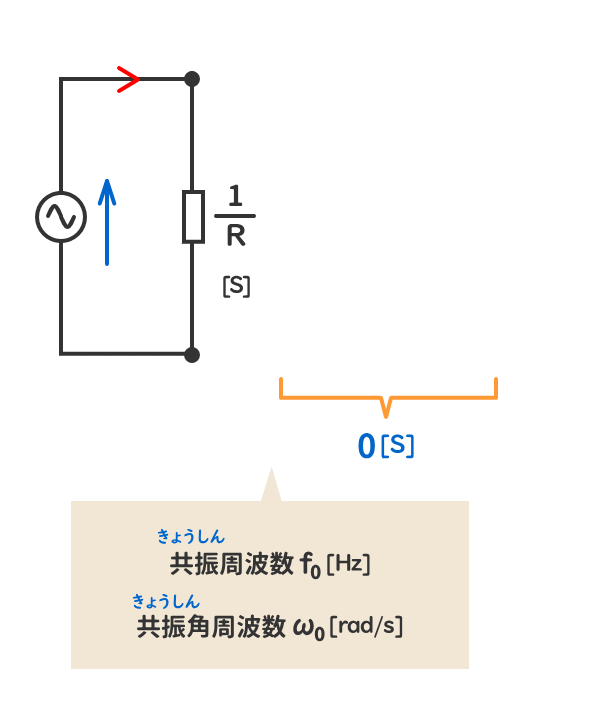
このときの回路の周波数を共振周波数f0[Hz]、角周波数を共振角周波数ω0[rad/s]という。
4.RLC直列交流回路の共振周波数f0[Hz]と共振角周波数ω0[rad/s]の公式の導出
RLC直列交流回路の複素インピーダンスの虚数部が0[Ω]という条件から、共振周波数f0[Hz]と共振角周波数ω0[rad/s]の公式の導出する。
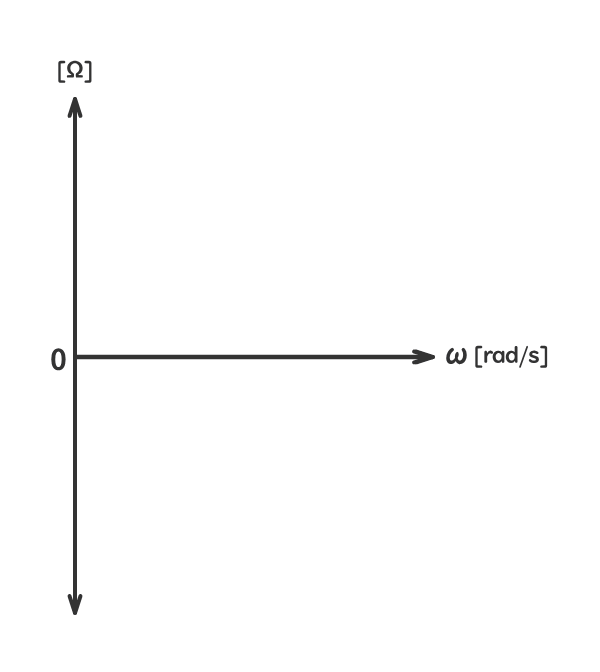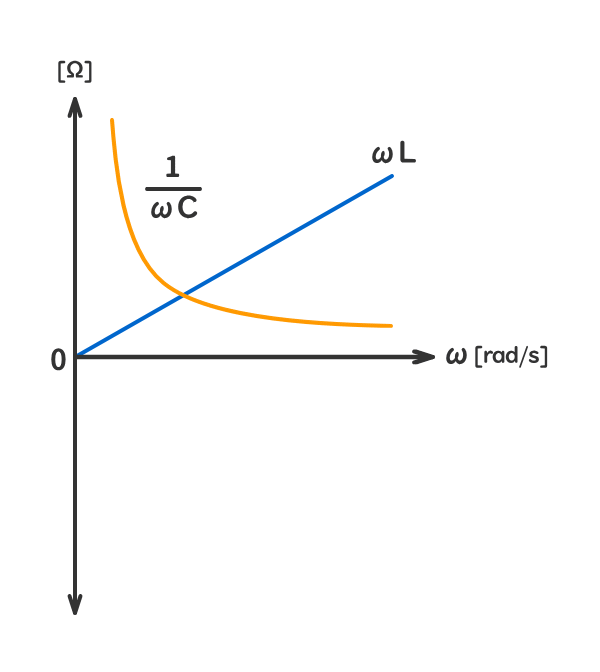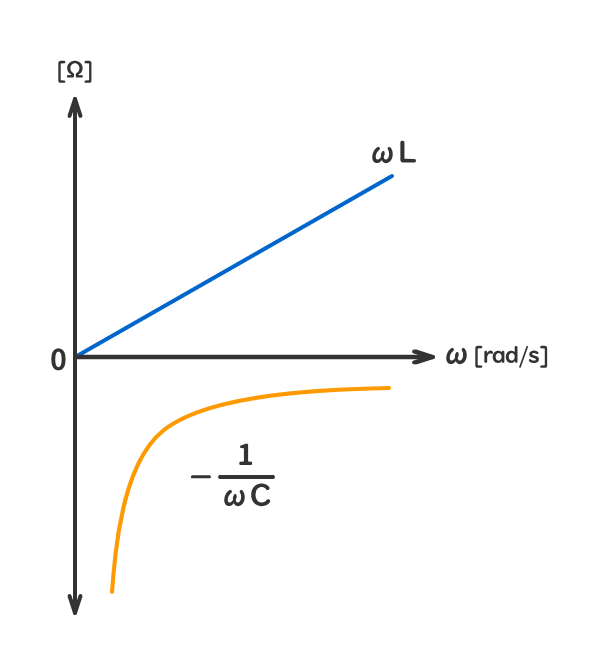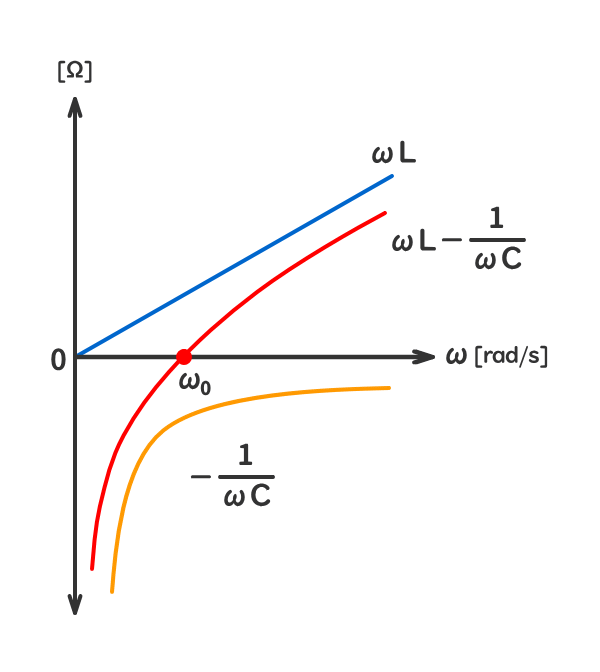
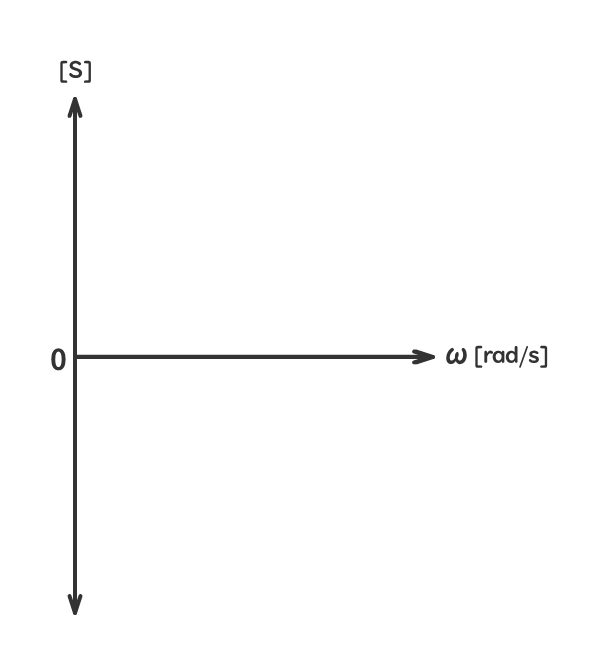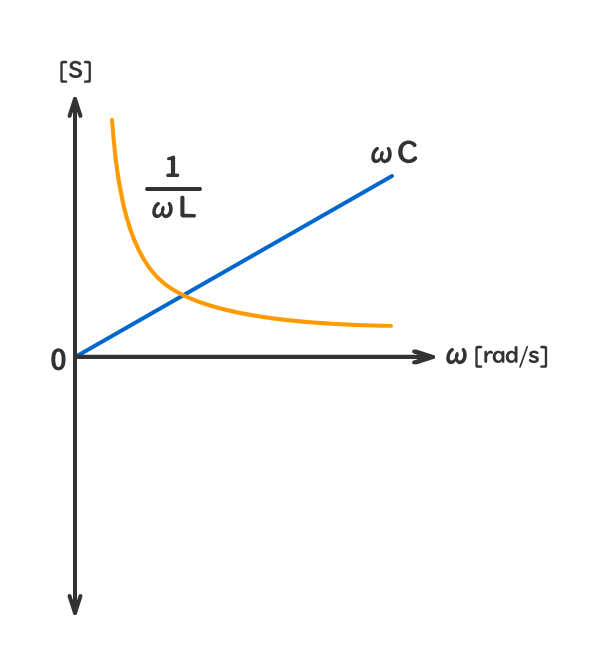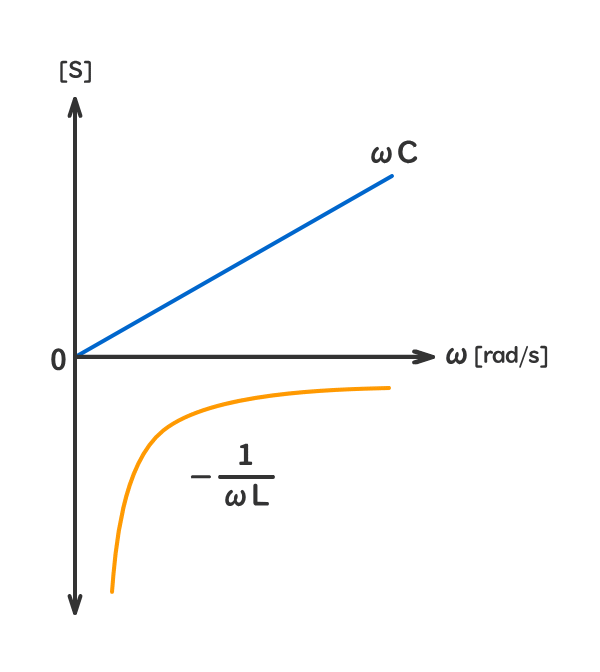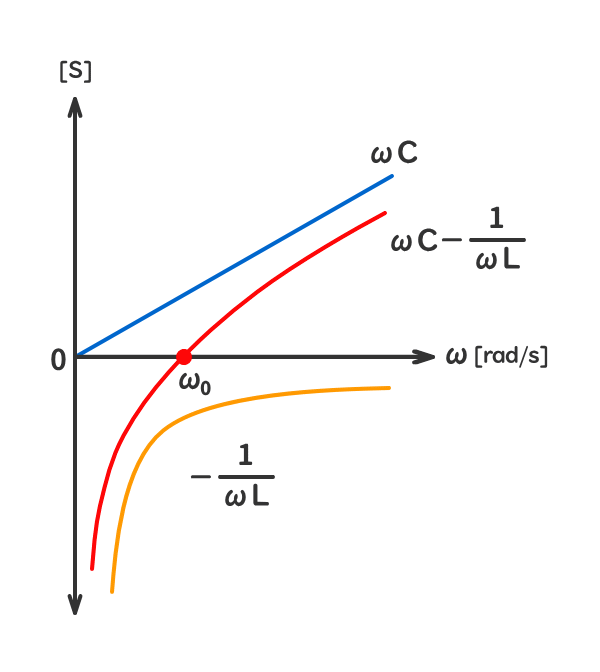
参考1:角周波数ω[rad/s]の変化に対する虚数部の変化
参考2:角周波数ω[rad/s]の変化に対する電流I[A]の変化
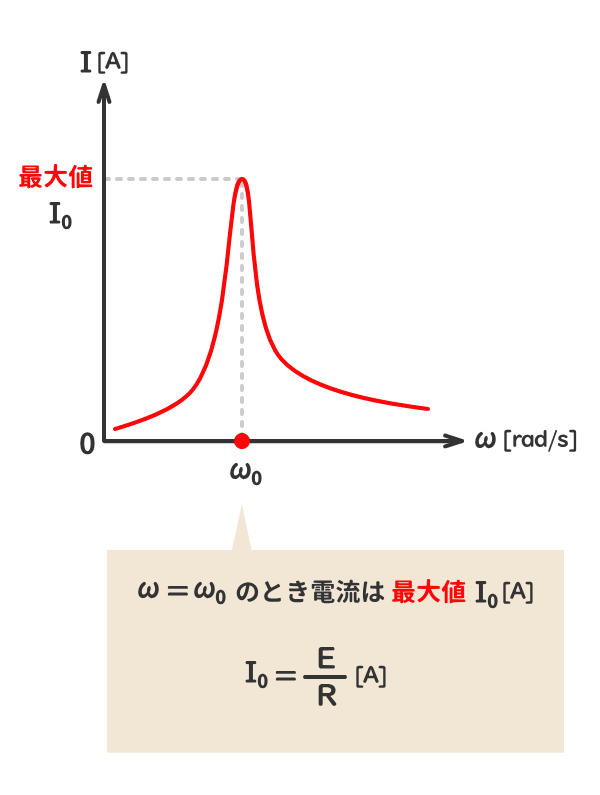
5.RLC並列交流回路の共振周波数f0[Hz]と共振角周波数ω0[rad/s]の公式の導出
RLC並列交流回路の複素アドミタンスの虚数部が0[S]という条件から、共振周波数f0[Hz]と共振角周波数ω0[rad/s]の公式の導出する。
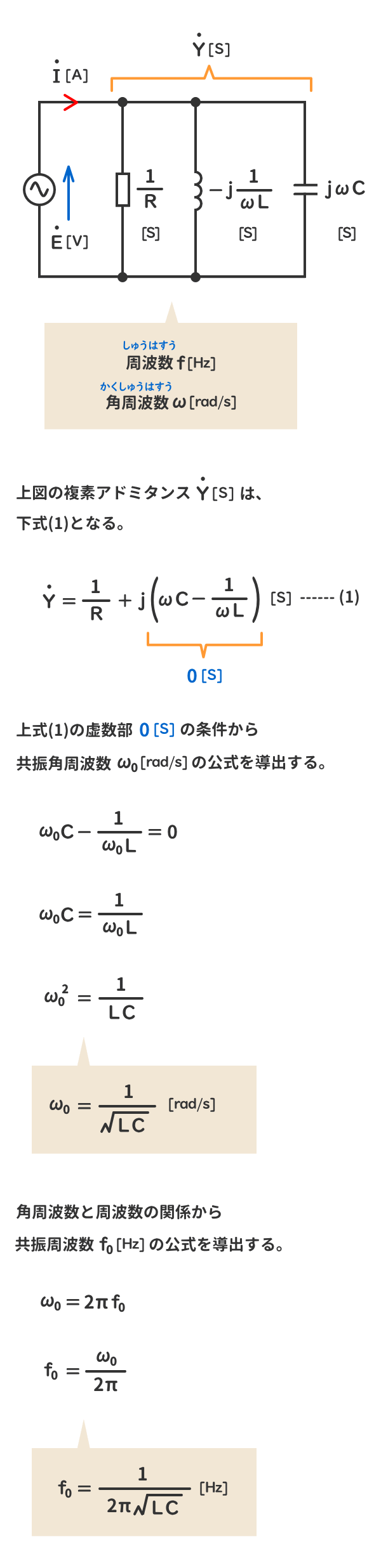
参考1:角周波数ω[rad/s]の変化に対する虚数部の変化
参考2:角周波数ω[rad/s]の変化に対する電流I[A]の変化

6.RLC直列交流回路とRLC並列交流回路の共振周波数f0[Hz]と共振角周波数ω0[rad/s]の公式は同形である。
共振周波数f0[Hz]と共振角周波数ω0[rad/s]の公式は、RLC直列交流回路でもRLC並列交流回路でも同じである。

例題1
下図のRLC直列交流回路の共振角周波数ω0[krad/s]と共振周波数f0[kHz]を求めよ。
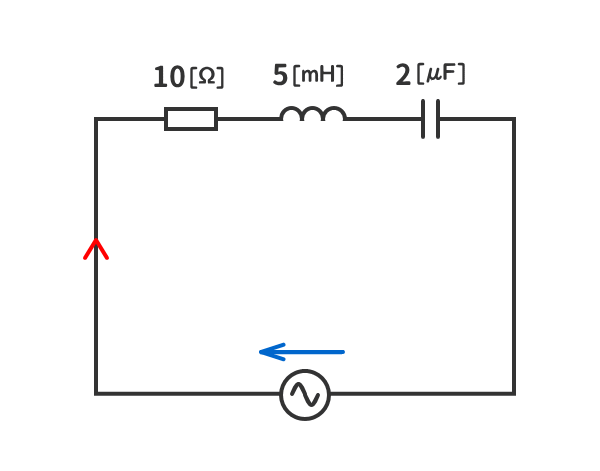
解答を表示する

解答を非表示にする
例題2
下図のRLC直列回路において、電流iと電圧eが同相(同位相)になっている。
このときの回路の状況を「共振」という用語を用いて簡単に説明しなさい。
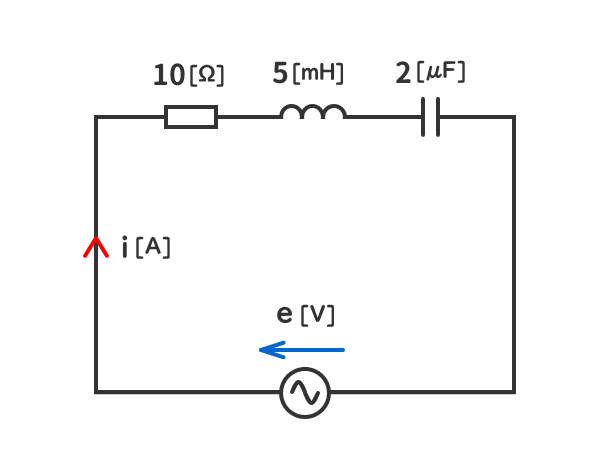
解答を表示する
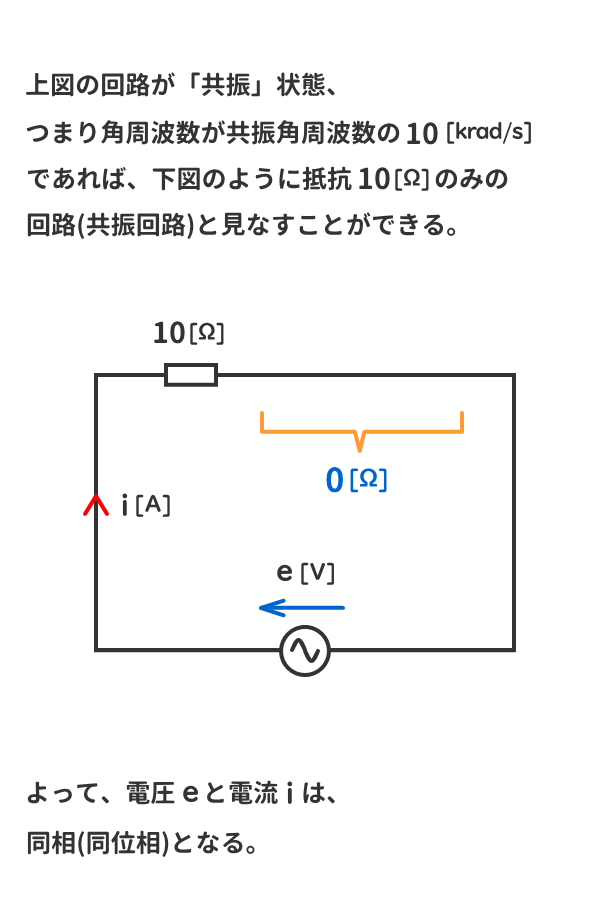
解答を非表示にする
例題3
下図のRLC並列交流回路の共振角周波数ω0[krad/s]と共振周波数f0[kHz]を求めよ。
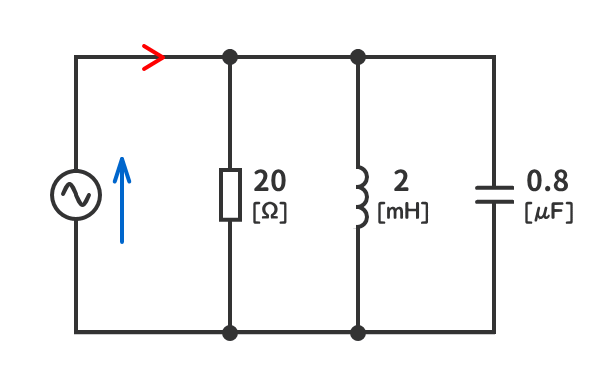
解答を表示する

解答を非表示にする
例題4
下図のRLC並列回路で角周波数ω[krad/s]を可変させた場合の電流Iの最小値[A]を求めよ。
ただしω≠0とする。

解答を表示する
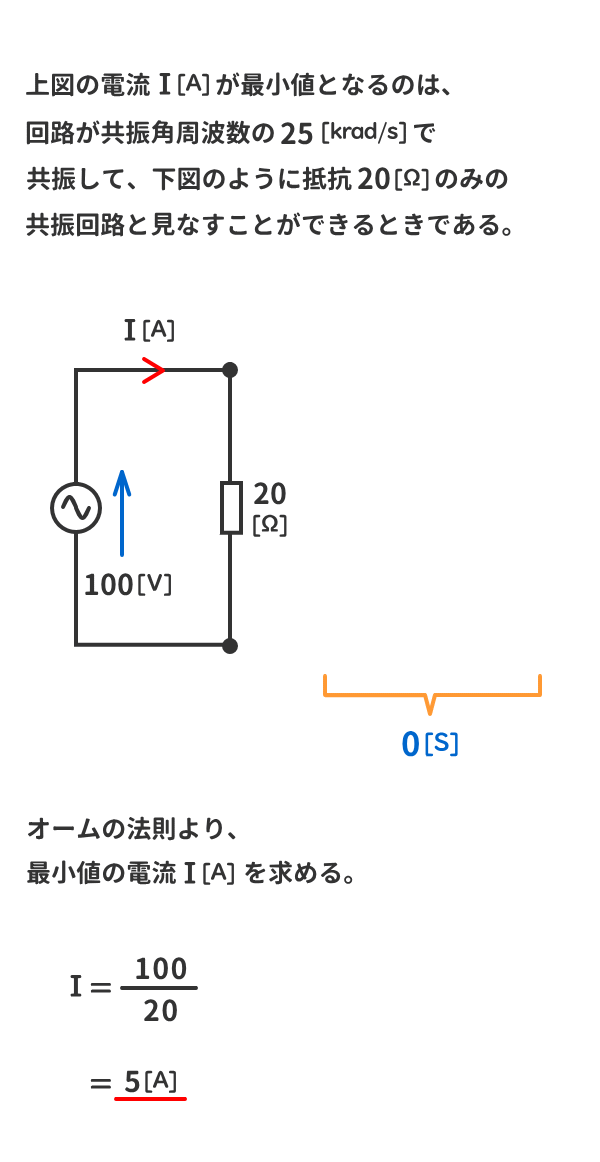
解答を非表示にする
7.電験3種の関連過去問






