過渡現象
過渡現象(かとげんしょう)とは、ある定常状態から別の定常状態に至るまでに起こる現象をいう。
定常状態とは安定した状態のことである。
過渡状態とは不安定な状態のことである。
目次
1. 過度現象は時間の経過で起こることを考える。
Aの食材がBのカレーになるには、調理の過程があるのは当然のことである。
さらに、調理の過程には時間の経過が伴うことも当然のことである。
過渡現象の大雑把なイメージとして、Aの安定している食材が、調理という不安定な状態を経て、Bの安定したカレーになったと考える。
この考えかたを、RL直列回路とRC直列回路で起こる過渡現象のイメージにつなげること。
2. RL直列回路の定常状態
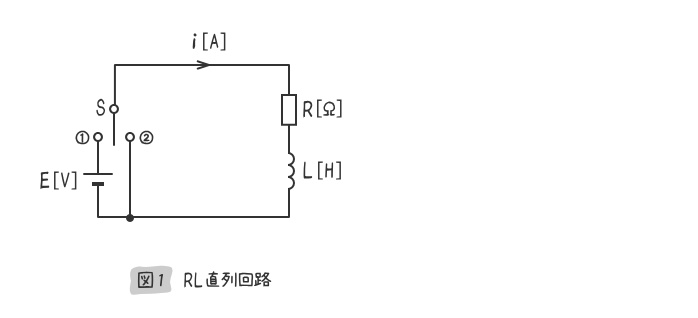
まずは、上図1のRL直列回路の定常状態を把握する。
直流回路の知識から、下記のことが分かる。
- スイッチSがOFFのときの定常状態
→ i=0 [A]
- スイッチSがON①のときの定常状態
→ i=E/R [A]
- スイッチSがON②のときの定常状態
→ i=0 [A]
3. RL直列回路の過渡現象
上図1のRL直列回路の過渡現象を考える。
ここでインダクタンスLは、現状の回路の定常状態を維持しようとする働きをすること及び、電気エネルギーを磁気エネルギーとして蓄えたり、磁気エネルギーを電気エネルギーとして放出したりする回路素子であることを念頭に置くこと。
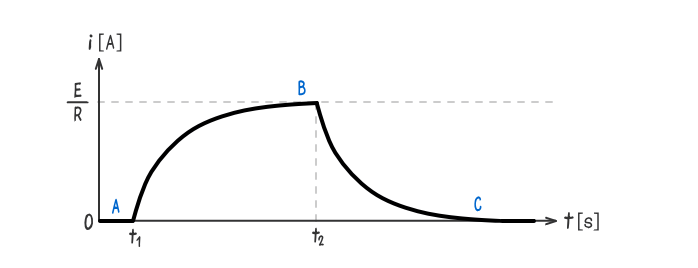
- 時刻t=t1[s]でスイッチSをON①に切り替えると、インダクタンスは現状の回路の定常状態Aを維持しようと働く。
よって、インダクタンスは開放状態となるので、電流i=0[A]である。
- 時刻t1[s]以降は、インダクタンスの開放状態が解消され始めるので、電流iは指数関数的に増加する。
インダクタンスが蓄える磁気エネルギーも増加する。
- 時刻t1[s]からの時間が、RL直列回路の時定数τ=L/R[s]より十分経過すれば、インダクタンスの開放状態は完全に解消される。
よって、電流i=E/R[A]の定常状態Bに移行する。
- 時刻t=t2[s]でスイッチSをON②に切り替えると、電源E[V]が無くなるので、インダクタンスは現状の回路の定常状態Bを維持しようと働く。
よって、蓄えた磁気エネルギーを放出するので、電流i=E/R[A]である。
- 時刻t2[s]以降は、インダクタンスが蓄えた磁気エネルギーが減少していくので、電流iは指数関数的に減少する。
- 時刻t2[s]からの時間が、RL直列回路の時定数τ=L/R[s]より十分経過すれば、蓄えた磁気エネルギーは完全に無くなる。
よって、電流i=0[A]の定常状態Cに移行する。
4. RL直列回路の過渡電流の公式
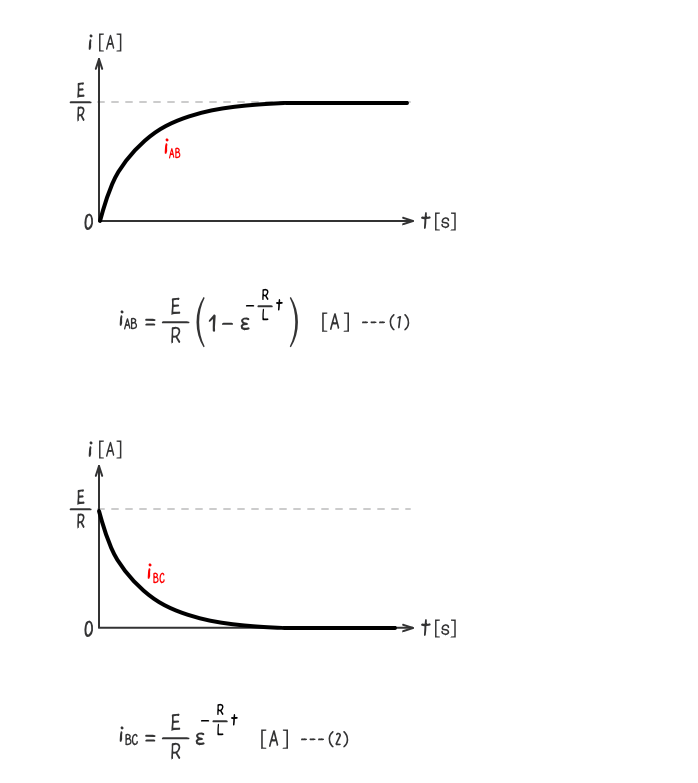
下式(1)と(2)のRL直列回路の過渡電流の公式は、微分方程式から導かれた結果である。
微分方程式の解き方を知っていたとしても、この公式は暗記しておく必要がある。
5. RL直列回路の時定数の公式
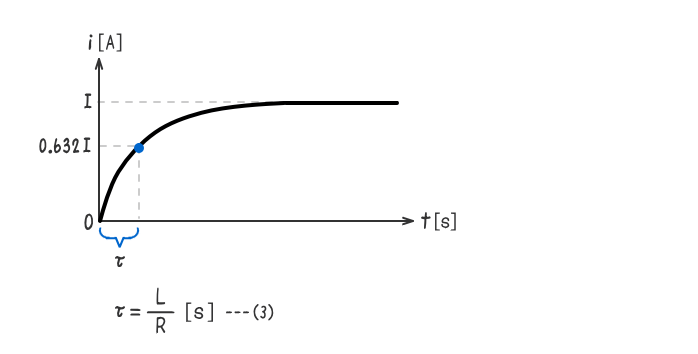
時定数(じていすう)とは、過渡現象に要する時間及びグラフの形状の目安となる定数である。
RL直列回路の時定数の公式は、下式(3)となる。
この公式の出典は、上式(1)(2)である。
1- ε-1=0.632
ε-1=0.368
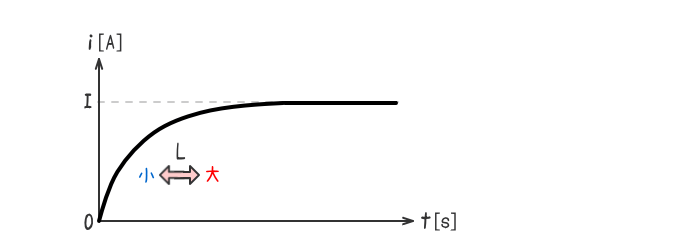
インダクタンスL[H]の値が大きいほど回路の定常状態を維持しようとする力が強くなる。
インダクタンスL[H]の値が小さいほど回路の定常状態を維持しようとする力が弱くなる。
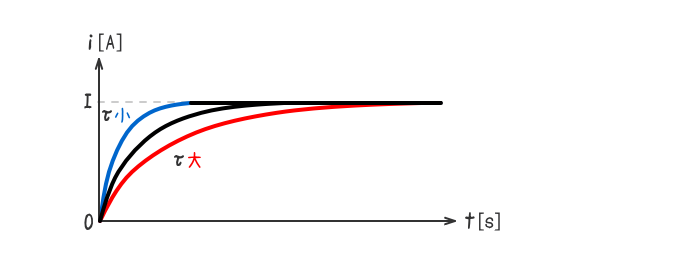
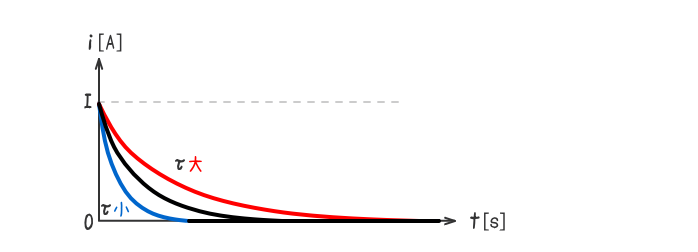
上述のことから、下図の時定数の変化によるグラフの形状の変化を把握すること。
6. RC直列回路の定常状態
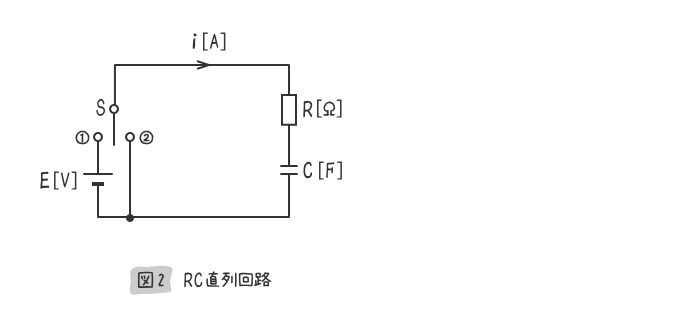
まずは、上図2のRC直列回路の定常状態を把握する。
直流回路の知識から、下記のことが分かる。
- スイッチSがOFFのときの定常状態
→ i=0 [A]
- スイッチSがON①のときの定常状態
→ i=0 [A]
- スイッチSがON②のときの定常状態
→ i=0 [A]
7. RC直列回路の過渡現象
上図2のRC直列回路の過渡現象を考える。
ここで静電容量Cは、現状の回路の定常状態を急変させる働きをすること及び、電気エネルギーを静電エネルギーとして蓄えたり、静電エネルギーを電気エネルギーとして放出したりする回路素子であることを念頭に置くこと。
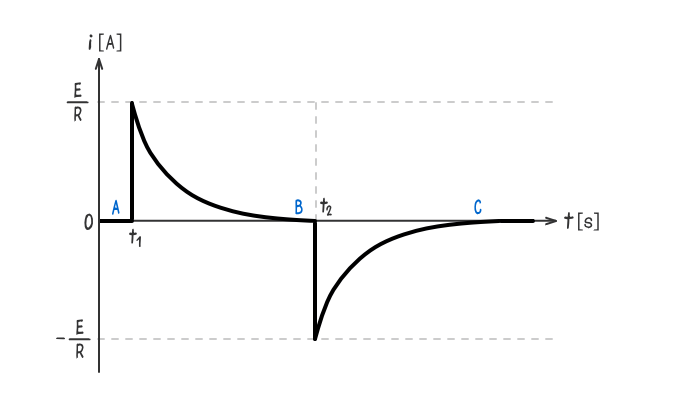
※コンデンサに蓄えられている初期電荷は0[C]とする。
- 時刻t=t1[s]でスイッチSをON①に切り替えると、静電容量は現状の回路の定常状態Aを急変させようと働く。
よって、静電容量は短絡状態となるので、電流i=E/R[A]である。
- 時刻t1[s]以降は、静電容量の短絡状態が解消され始めるので、電流iは指数関数的に減少する。
静電容量が蓄える静電エネルギーは増加する。(充電が進むので電流減少・エネルギ―増加と解釈)
- 時刻t1[s]からの時間が、RC直列回路の時定数τ=CR[s]より十分経過すれば、静電容量の短絡状態は完全に解消される。(充電完了)
よって、電流i=0[A]の定常状態Bに移行する。
- 時刻t=t2[s]でスイッチSをON②に切り替えると、電源E[V]が無くなるので、静電容量は現状の回路の定常状態Bを急変させようと働く。
よって、蓄えた静電エネルギーを放出するので、電流i=-E/R[A]である。(-記号は充電電流とは逆方向の電流であることを意味する。)
- 時刻t2[s]以降は、静電容量が蓄えた静電エネルギーが減少していくので、電流iは指数関数的に減少する。
- 時刻t2[s]からの時間が、RC直列回路の時定数τ=CR[s]より十分経過すれば、蓄えた静電エネルギーは完全に無くなる。
よって、電流i=0[A]の定常状態Cに移行する。
8. RC直列回路の過渡電流の公式
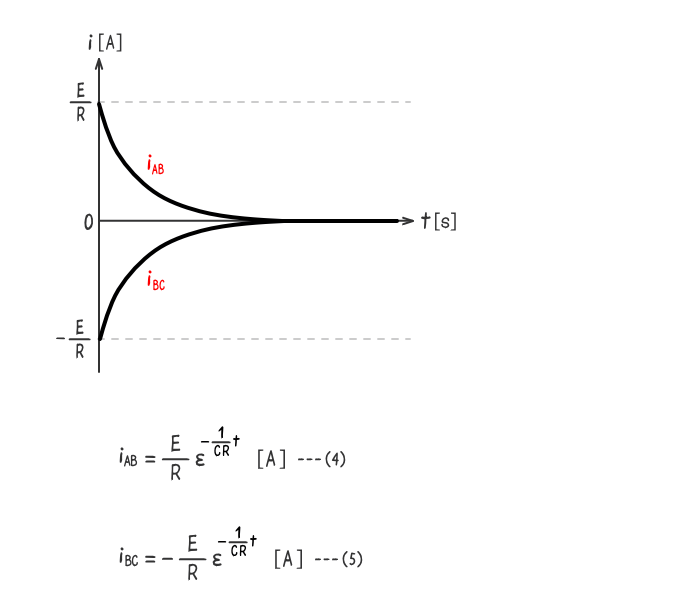
下式(4)と(5)のRC直列回路の過渡電流の公式は、微分方程式から導かれた結果である。
微分方程式の解き方を知っていたとしても、この公式は暗記しておく必要がある。
9. RC直列回路の時定数の公式
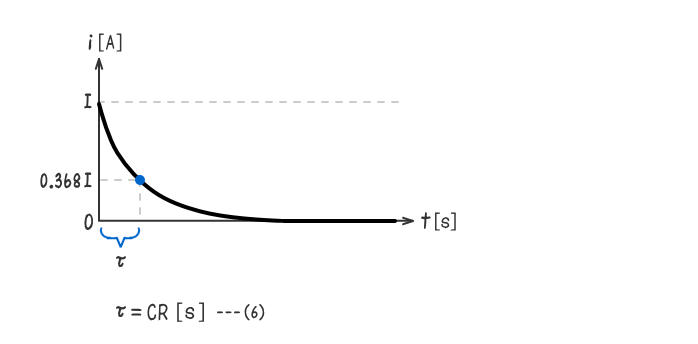
時定数(じていすう)とは、過渡現象に要する時間及びグラフの形状の目安となる定数である。
RC直列回路の時定数の公式は、下式(6)となる。
この公式の出典は、上式(4)(5)である。
ε-1=0.368
静電容量C[F]の値が大きいほど回路の定常状態を急変させようとする力が強くなる。
静電容量C[F]の値が小さいほど回路の定常状態を急変させようとする力が弱くなる。
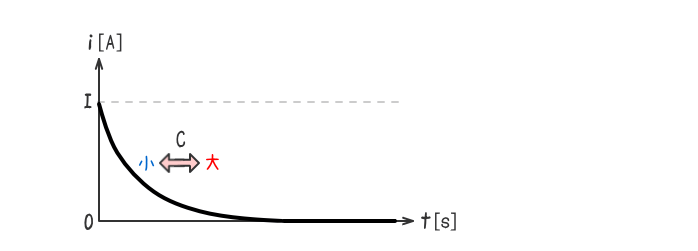
上述のことから、下図の時定数の変化によるグラフの形状の変化を把握すること。
例題1
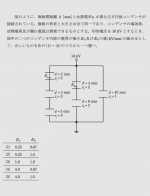
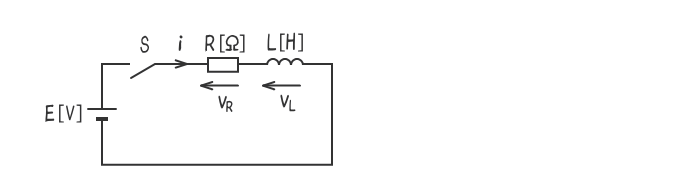
下図のように、開いた状態のスイッチS、抵抗R[Ω]、インダクタンスL[H]のコイル、直流電源E[V]からなる直流回路がある。
この直流回路において、スイッチSを閉じた直後に過渡現象が起こる。この場合に、回路の電流i、端子電圧vR及びvLに関し、時間の経過に従って起こる過渡現象として正しいものを組み合わせたのは次のうちどれか。
〔電験3種/平成20年度/理論問10一部改定〕
| 電流i | 端子電圧vR | 端子電圧vL | |
| 1 | 大きくなる | 低下する | 上昇する |
| 2 | 小さくなる | 上昇する | 低下する |
| 3 | 大きくなる | 上昇する | 上昇する |
| 4 | 小さくなる | 低下する | 上昇する |
| 5 | 大きくなる | 上昇する | 低下する |
解答を表示する

解答を非表示にする
例題2
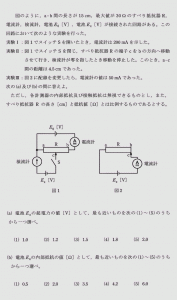
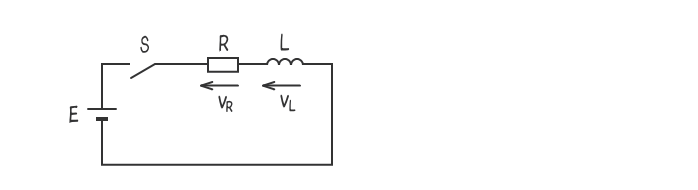
下図のように、抵抗RとインダクタンスLのコイルを直列に接続した回路がある。
この回路において、スイッチSを時刻t=0で閉じた場合に流れる電流及び各素子の端子電圧に関する記述として、誤っているのは次のうちどれか。
〔電験3種/平成17年度/理論問9一部改定〕
- この回路の時定数は、Lの値に比例している。
- Rの値を大きくすると、この回路の時定数は小さくなる。
- スイッチSを閉じた瞬間(時刻t=0)の端子電圧VLの大きさは、零である。
- 抵抗Rの端子電圧VRの大きさは、定常状態では電源電圧Eの大きさに等しくなる。
- 定常状態の電流は、Lの値に関係しない。
解答を表示する

解答を非表示にする
例題3
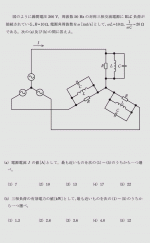
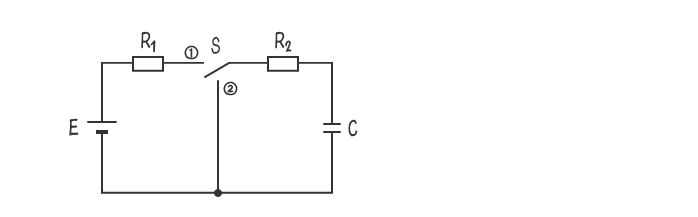
下図のような回路において、スイッチSを①側に閉じて、回路が定常状態に達した後で、スイッチSを切り換え②側に閉じた。
スイッチS、抵抗R2及びコンデンサCからなる閉回路の時定数の値として、正しいのは次のうちどれか。
ただし、抵抗R1=300[Ω]、抵抗R2=100[Ω]、コンデンサCの静電容量=20[μF]、直流電圧E=10[V]とする。
〔電験3種/平成18年度/理論問10〕
- 0.05[μs]
- 0.2[μs]
- 1.5[ms]
- 2.0[ms]
- 8.0[ms]
解答を表示する

解答を非表示にする