小数点の移動に伴う計算処理の仕方
ある数の小数点を移動させる場合、きちんと処理しないと、移動の前後で数が合わなくなってしまう。

上の計算処理の意味をあやふやなままにしておくと、単位変換のとにミスを犯すことがある。
自信を持って計算処理をするために意味を理解しておこう。
1.準備
①ある数に10nをかけた数は、ある数の小数点を右にn桁移動させた数と同じである。
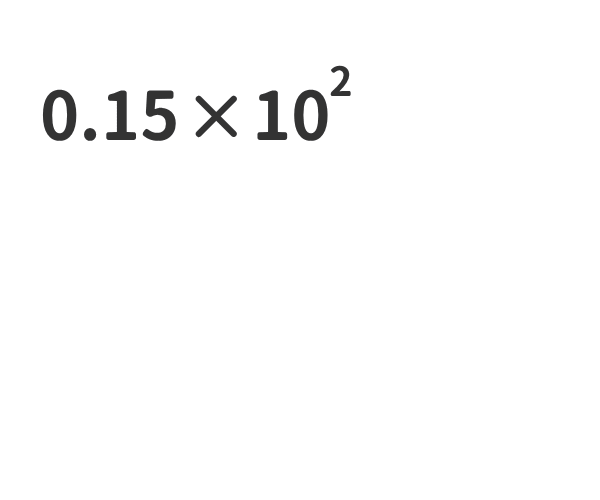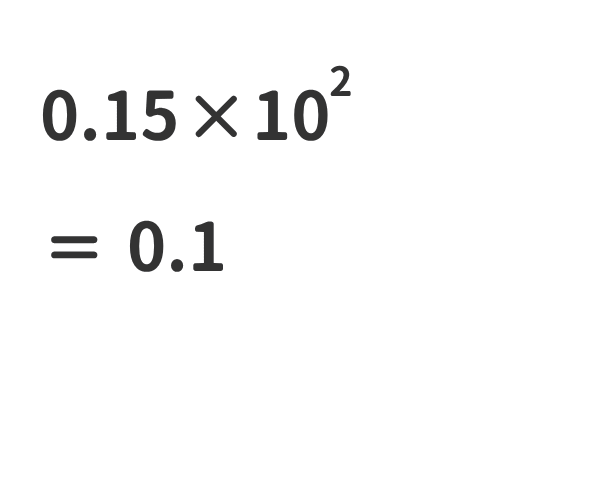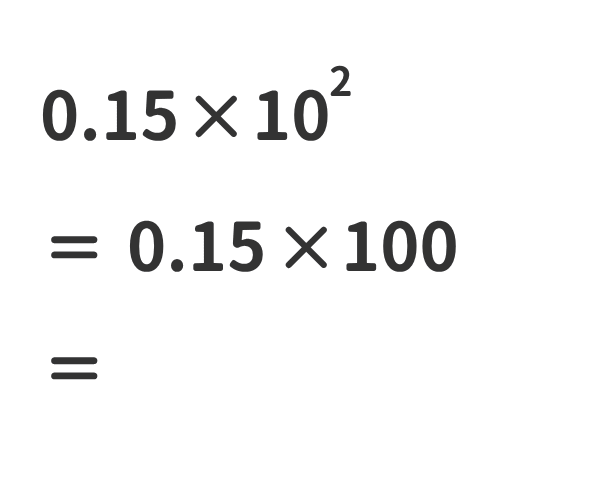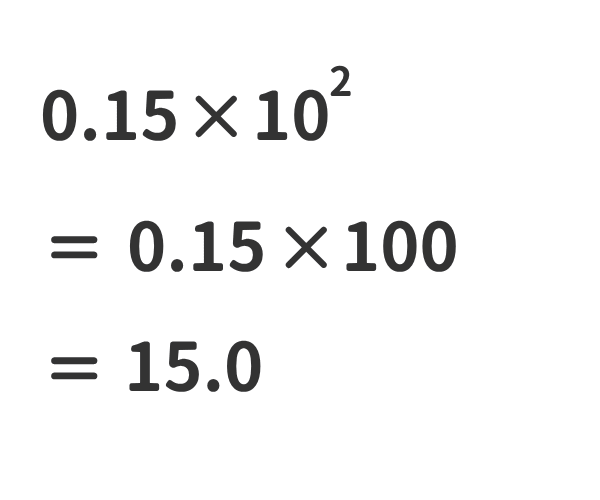
②ある数に10-nをかけた数は、ある数の小数点を左にn桁移動させた数と同じである。
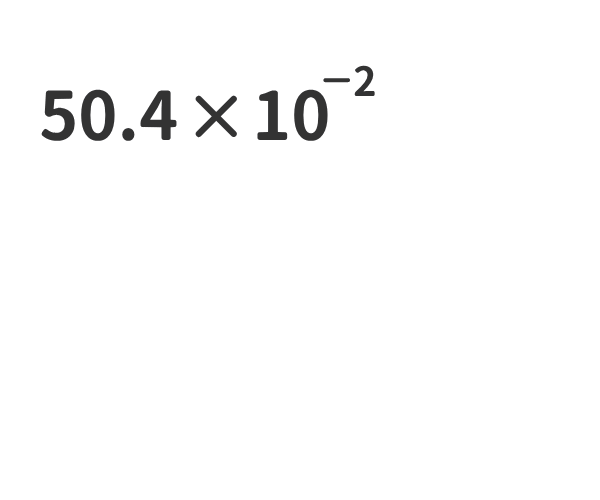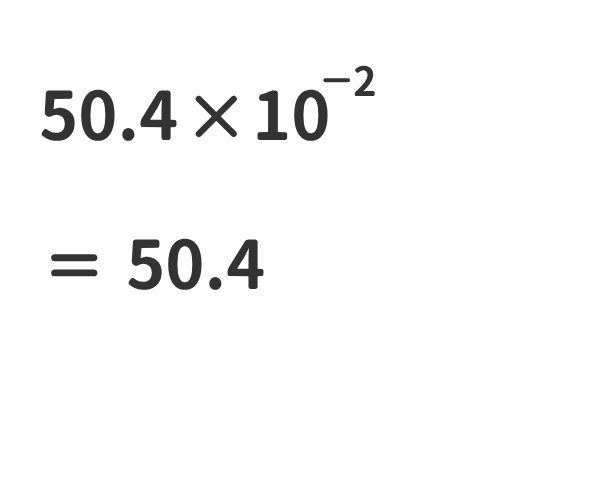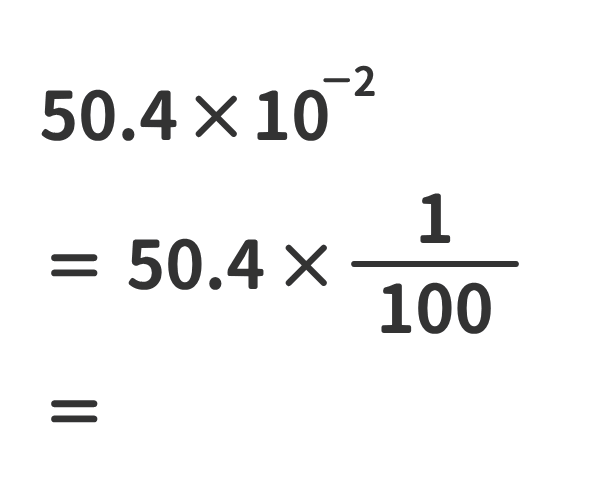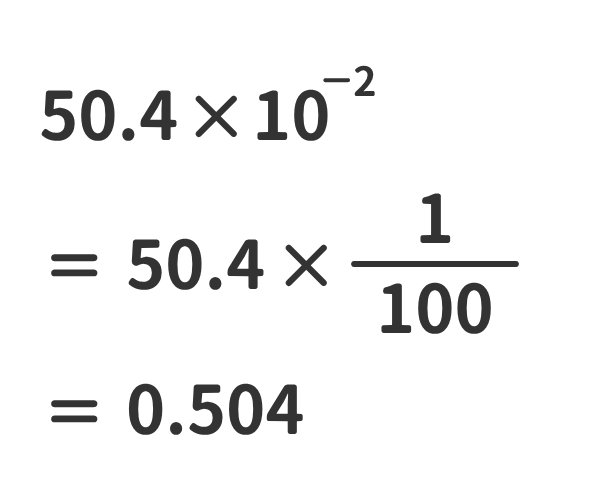
③ある数に1をかけても数は変わらない。

2.小数点の移動に伴う計算処理の考え方
前項①、②、③の関係を利用すると、小数点を自由自在に移動させることができるようになる。
0.3141の小数点を「右に3桁」移動させる場合の考え方。

720.8の小数点を「左に3桁」移動させる場合の考え方。

3.実用的な小数点の移動処理
意味を理解あとは次のように小数点の移動処理をしよう。ある数の小数点を右にn桁移動させる場合は、数が大きくなるので、10-nを掛けて数の帳尻を合わせる。

ある数の小数点を左にn桁移動させる場合は、数が小さくなるので、10nを掛けて数の帳尻を合わせる。

4.単位変換の例
ここでは、「長さ・面積・体積」の単位の変換例を示しておきます。指数法則とSI接頭語の知識が必須となります。
関連記事:指数法則を暗記しよう!
関連記事:SI接頭語を暗記しよう!
3000[mm]を[cm]で表しなさい。
\(\\\Large3000[mm] \\\Large=3000\times10^{-3}[m] \\\Large=3000\times10^{-1}\times10^{-2}[m] \\\Large=3000\times10^{-1}[cm] \\\Large=300[cm]\)
5[cm2]を[m2]で表しなさい。
\(\\\Large5[(cm)^2] \\\Large=5[c^2m^2] \\\Large=5\times(10^{-2})^2[m^2] \\\Large=5\times10^{-4}[m^2]\)
1000000[cm3]を[m3]で表しなさい。
\(\\\Large1000000[(cm)^3] \\\Large=1000000[c^3m^3] \\\Large=1000000\times(10^{-2})^3[m^3] \\\Large=1000000\times10^{-6}[m^3] \\\Large=1[m^3]\)





