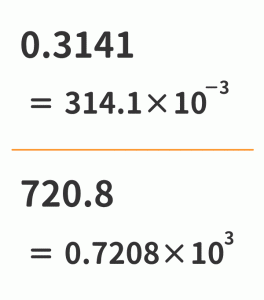連立方程式の解き方
1.連立方程式とは
連立方程式とは、二つ以上の方程式を組み合わせたものをいう。
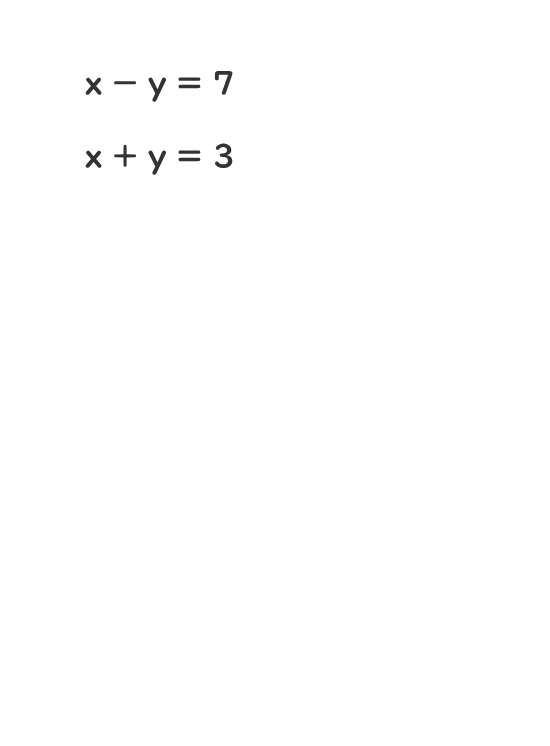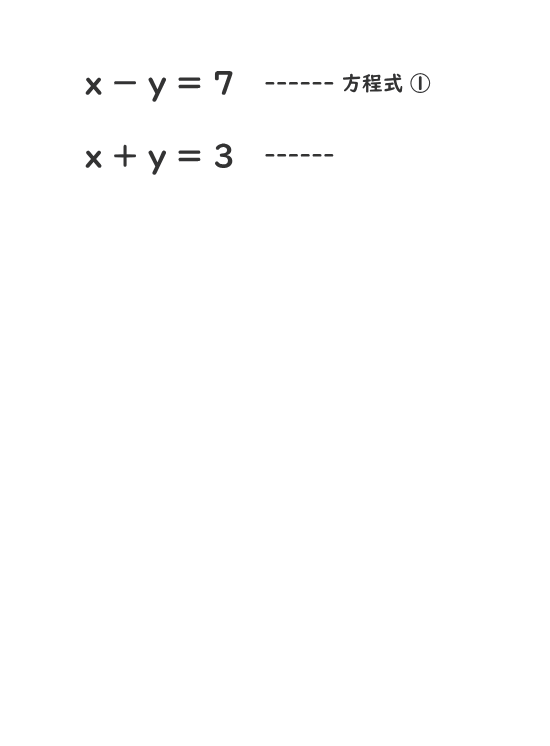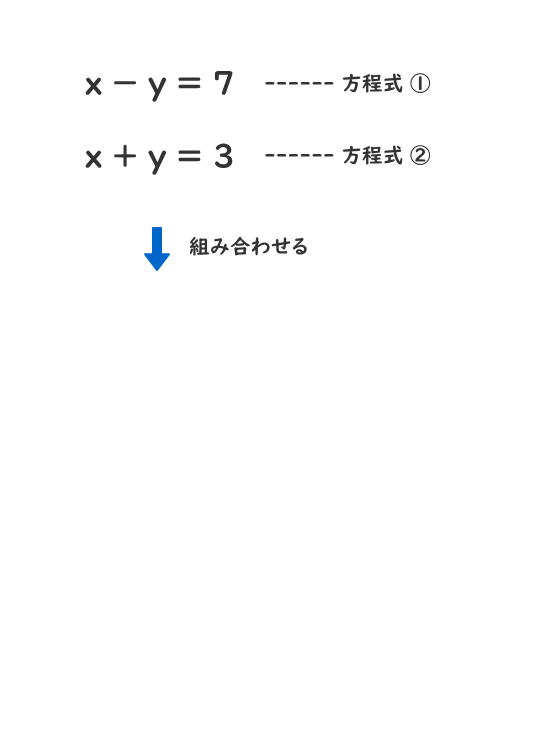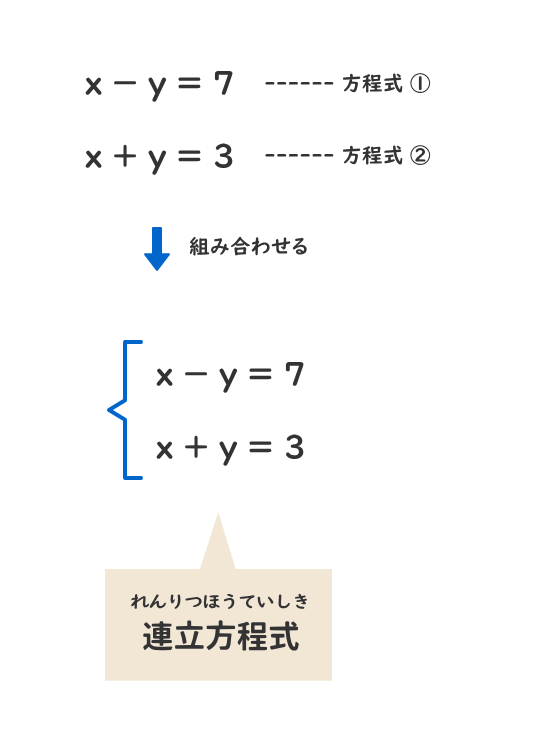
2.連立方程式の解とは
連立を組んでいる全ての方程式が受け入れられるものが連立方程式の解になる。
一部の方程式を満たすだけでは連立方程式の解とはいえない。
一部の方程式を満たすだけでは連立方程式の解とはいえない。

例えば、x=8とy=1は方程式①を満たすが、方程式②を満たさないので、連立方程式の解とはいえない。
3.方程式と等式
方程式とは、未知数を含んだ等式をいう。
方程式の未知数がある決まった値をとるときに等式が成立する。

ちなみに、上式の方程式の解は、x=3である。

等式とは、等号(=)で結ばれた式をいう。
等式に未知数が含まれている場合が方程式である。
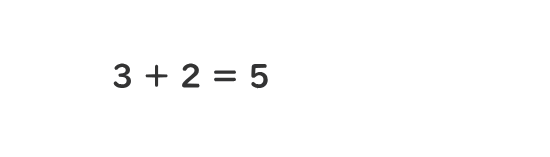
4.未知数と既知数
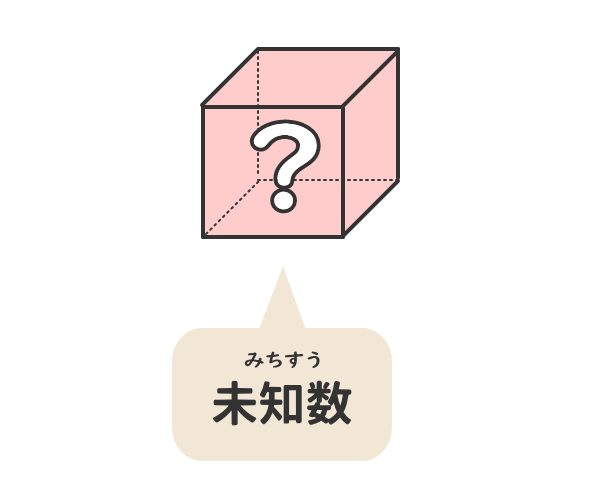
未知数とは、分かっていない数のことである。
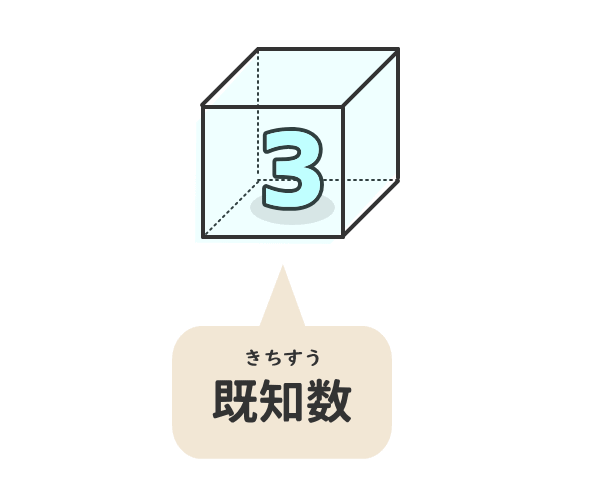
既知数とは、分かっている数のことである。
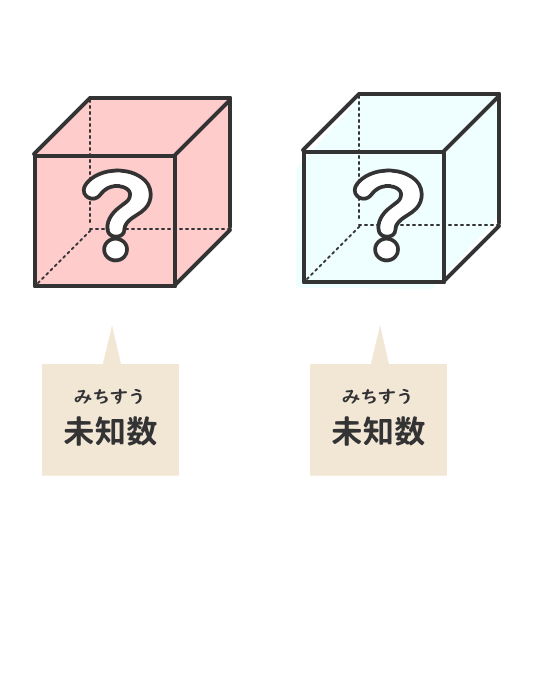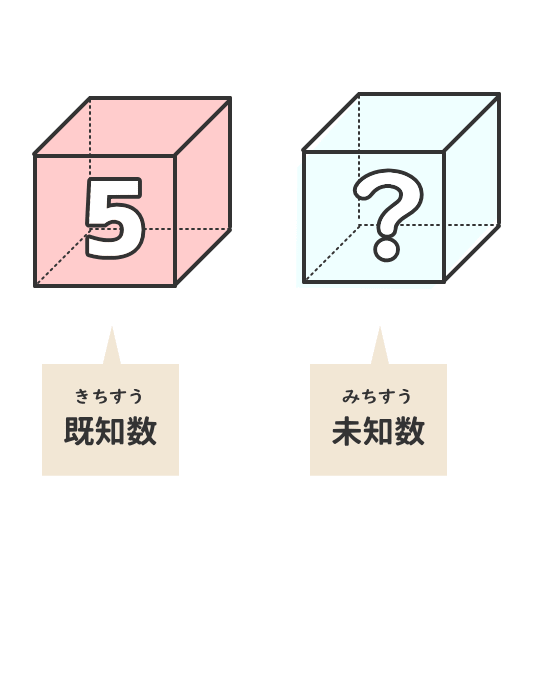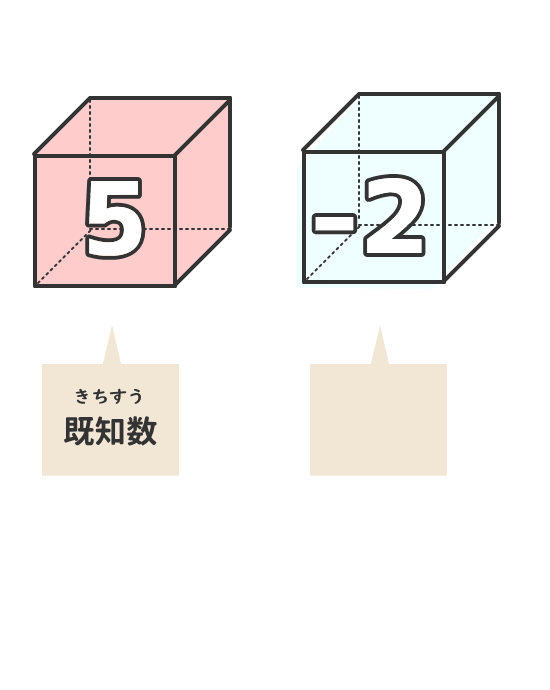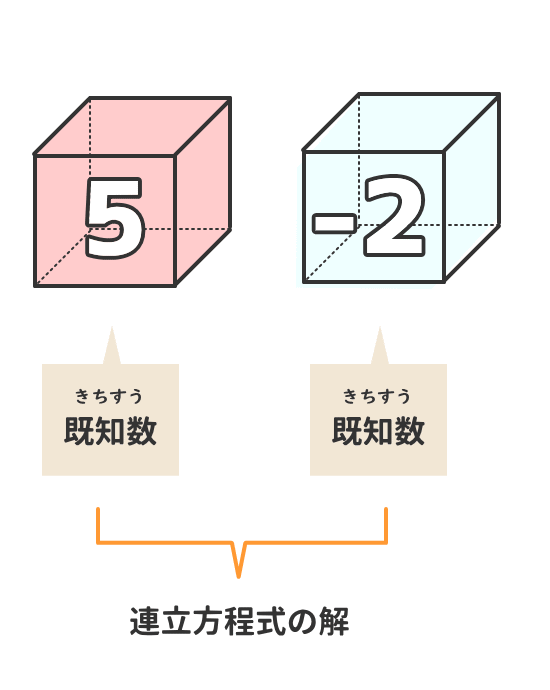
5.連立方程式の解を求める手順
連立方程式の解を求める手順は、未知数を順番に消していって、既知数に変えていくだけである。
連立方程式の解を求めるための具体的な方法として、加減法と代入法の二つの方法がある。
6.加減法による連立方程式の解を求める手順

7.代入法による連立方程式の解を求める手順
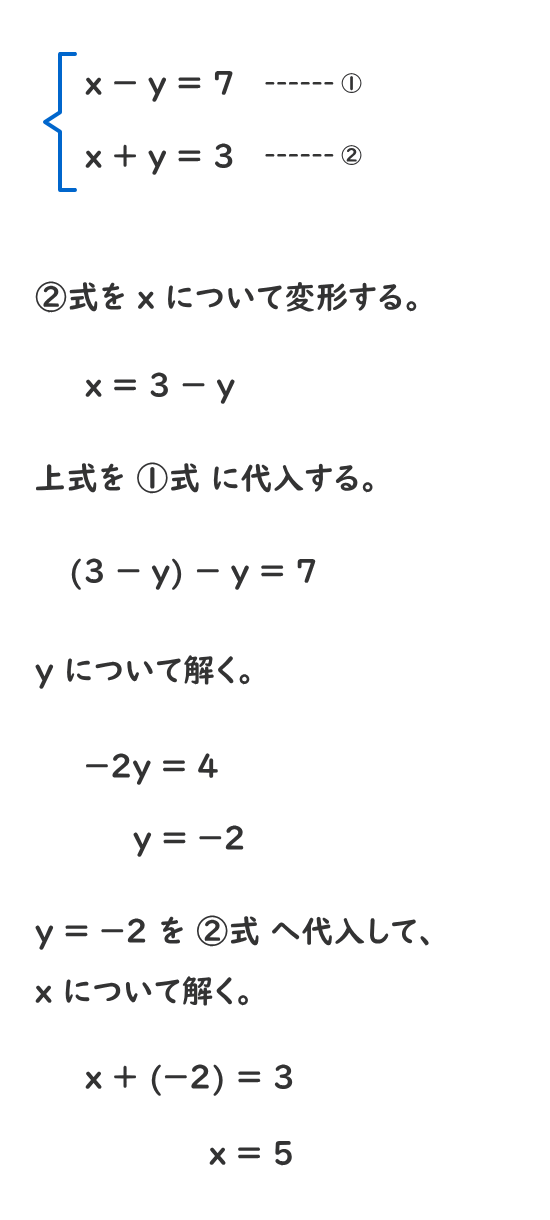
8.連立方程式は加減法と代入法を組み合わせて解くのが効率がよい。