令和元年度電力問17の問題と解答

解答を表示する

解答を非表示にする
令和元年度電力問17の解答ポイント
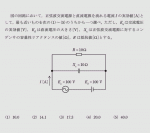
- 下図のような三相3線式配電線路の概略図を書き、問題の条件に基づいた諸量の値や文字記号を書いて状況を把握する。
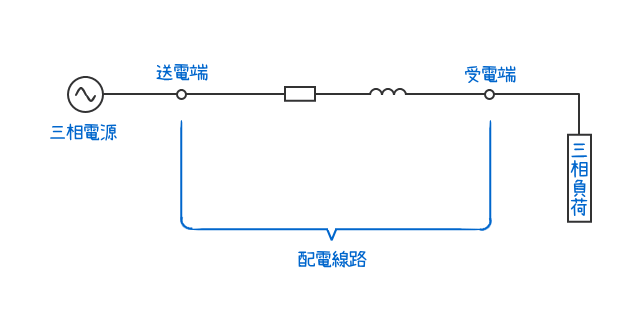
- 三相交流回路の有効電力の公式
$${P=}\sqrt{3}{VIcosθ}\quad [W]$$
$$\begin{eqnarray}{P} &:& 三相有効電力[W]\\\\{V} &:& 線間電圧[V]\\\\{I} &:& 線電流[A]\\\\{cosθ} &:& 力率\end{eqnarray}$$
- 三相3線式送配電線路の線路電圧降下率ε降下[%]の定義式
$${ε_{降下}=}\frac{V_s-V_r}{V_r}{×100}\quad [%]$$
$$\begin{eqnarray}{ε_{降下}} &:& 線路電圧降下率[%]\\\\{V_s} &:& 送電端(電源側)の線間電圧[V]\\\\{V_r} &:& 受電端(負荷側)の線間電圧[V]\end{eqnarray}$$
- 三相3線式送配電線路の線路電圧降下Vs-Yrの近似式
$${V_s-V_r=}\sqrt{3}{I(rcosθ+xsinθ)}\quad [V]$$
$$\begin{eqnarray}{V_s} &:& 送電端(電源側)の線間電圧[V]\\\\{V_r} &:& 受電端(負荷側)の線間電圧[V]\\\\{I} &:& 線電流[A]\\\\{cosθ} &:& 負荷力率\end{eqnarray}$$
- 下記の三角関数の数値関係は、cos2θ+sin2θ=1の公式を適用しなくても即座に書き出せるようにしておく必要がある。
$${cosθ=0.8}\quad{↔}\quad{sinθ=0.6}$$
$${cosθ=0.6}\quad{↔}\quad{sinθ=0.8}$$
$${cosθ=1}\quad{↔}\quad{sinθ=0}$$
- 参考「計算問題ポイント集:電力系統」
- 関連過去問題:平成26年度電力問7