平行板コンデンサ
二つの導体間の静電容量を利用して電荷を蓄える素子をコンデンサといい、平行板コンデンサが最も基本的なコンデンサである。
目次
1. コンデンサの基礎知識
- 導体(どうたい)とは、電気抵抗が非常に小さく、電流(電荷)が流れやすい物質をいう。
- 金、銀、銅、アルミニウムは、導体である。

- 絶縁体(ぜつえんたい)とは、電気抵抗が非常に大きく、電流(電荷)が流れにくい物質をいう。
- ゴム、プラスチック、紙、油、空気は絶縁体である。

- 絶縁破壊とは、絶縁体が破壊されて電気抵抗が小さくなり、電流が流れる状態になることをいう。
- コップのような形状の容器に水が蓄えられるのと同じように、電荷を蓄えることができる形状がある。
- 容器の容量が大きくなれば多くの水を蓄えることができる。
- 導体である平行板の極板は、電荷を蓄えることができる形状である。
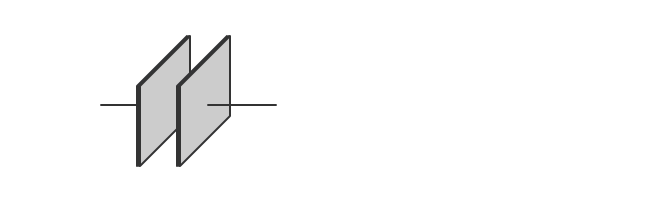
- コンデンサの電荷を蓄える能力を表したものが、静電容量である。
- [V]の単位は、「ボルト」と読む。
- [C]の単位は、「クーロン」と読む。
- [F]の単位は、「ファラド」と読む。
- [H]の単位は、「ヘンリー」と読む。
- εは、「イプシロン」と読む。
2. 平行板コンデンサの形状を変えると蓄えられる電荷を増やことができる。
下図1の形状では、電荷を蓄えることができなかった。
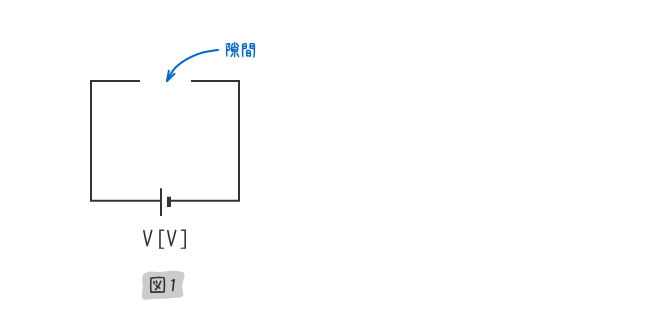
下図2のように、上図1の隙間を二枚の極板で平行に挟むと、電荷を蓄えることができた。
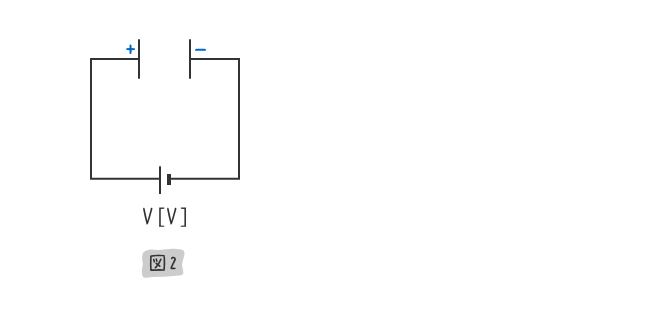
下図3のように、上図2の極板間の距離を縮めたところ、蓄えられる電荷を増やすことができた。
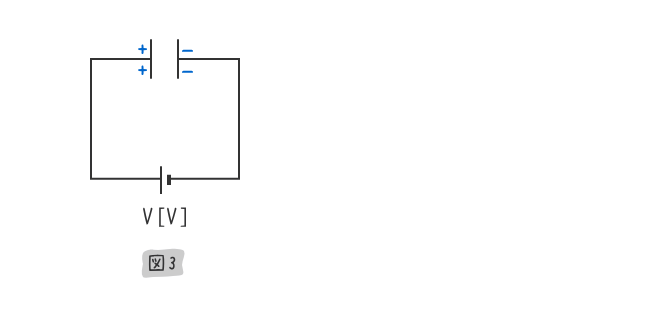
下図4のように、上図3の極板の面積を広げたところ、蓄えられる電荷を増やすことができた。
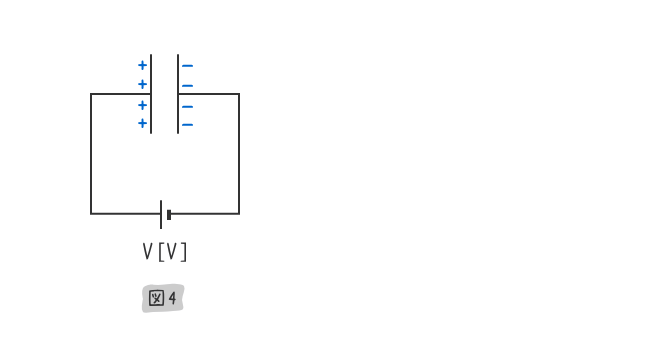
下図5のように、上図4の極板間に紙や油などの絶縁体を挿入したところ、蓄えられる電荷を増やすことができた。
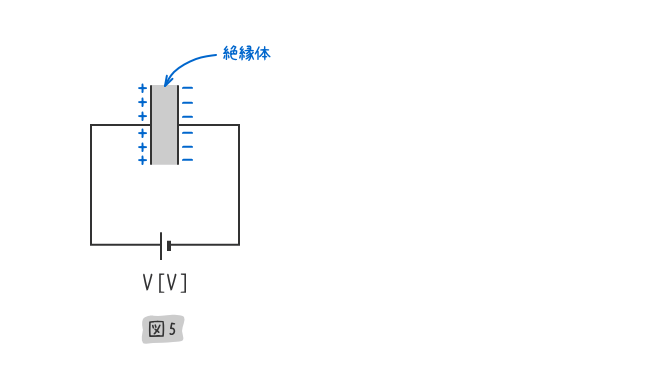
3. 平行板コンデンサに蓄えられる電荷と静電容量と電圧の関係式
下図6のように、コンデンサの形状は変えずに電源電圧を高くしたところ、図7のグラフの様に蓄えられる電荷は電圧に比例して増えていった。
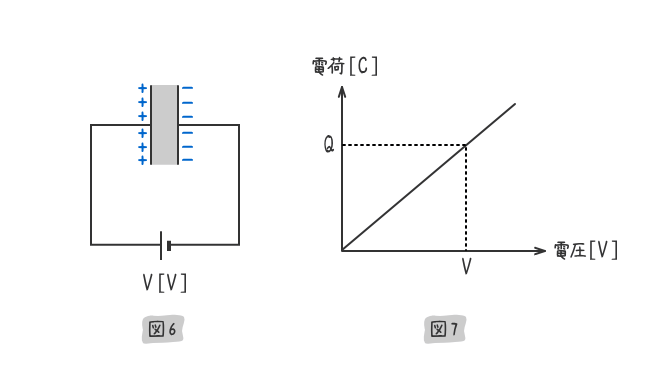
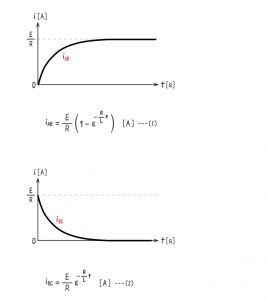
ゆえに、平行板コンデンサに蓄えられる電荷と静電容量と電圧の関係式は、下式(1)で表すことができる。

上式(1)と(2)は、コンデサの形状に関係なく成立する一般式である。
(1)式から、電源電圧を2倍にすれば、コンデンサに蓄えられる電荷も2倍になることが分かる。
ただし、電圧を高くすると極板間の絶縁体(誘電体)が絶縁破壊を起こすので、際限なく電荷を蓄えることはできない。
静電容量の大きいコンデンサであれば、電圧が低くても多くの電荷を蓄えることができる。
4. 平行板コンデンサの静電容量の式
平行板コンデンサの静電容量は、二枚の極板間の誘電率と極板面積に比例し、極板間距離に反比例する。
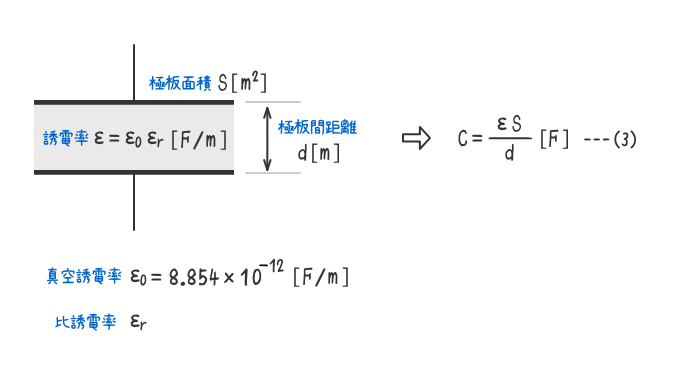
5. 平行板コンデンサに蓄えられる静電エネルギー
下図8の平行板コンデンサに蓄えられる静電エネルギーW[J]は、下図9の黄色の三角形の面積に相当する。
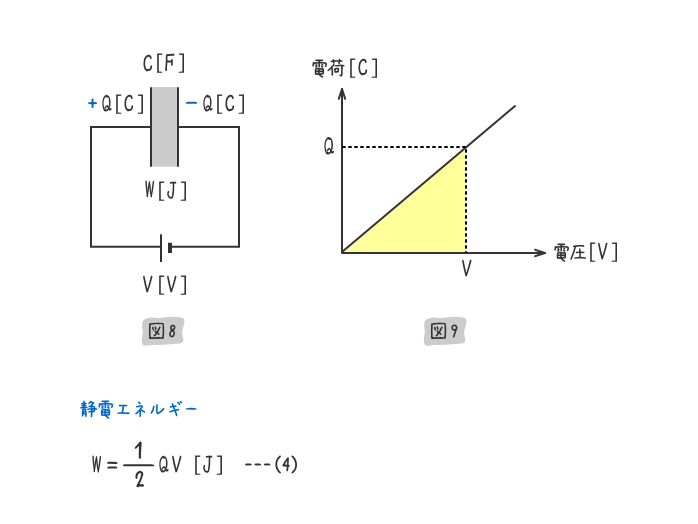
上式(4)は、(1)式から下式(5)のように書くことができる。
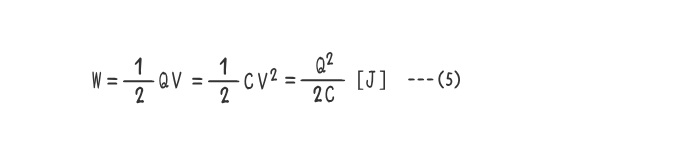
上式(5)は、コンデサの形状に関係なく成立する一般式である。
例題1
極板間距離が8.854[mm]、極板面積が100[cm2]、比誘電率2の平行板コンデンサがある。
この平行板コンデンサ静電容量[pF]の値を求めよ。
ただし、真空誘電率を8.854×10-12[F/m]とする。
解答を表示する

解答を非表示にする
例題2
静電容量が2[μF]のコンデンサがある。
このコンデンサに直流電源100[V]を接続して充電を開始した。
充電が完了したときのコンデサに蓄えられる電荷[C]と静電エネルギー[J]の値を求めよ。
ただし、コンデンサの形状は問わないものとする。
解答を表示する

解答を非表示にする