「サイト内お気に入り」に登録する

水力発電所は、下図のように、水が高い所にある場合に保有する①「位置エネルギー」を水車で②「回転エネルギー」に変換した後に、発電機で③「電気エネルギー」に変換している。

 

 

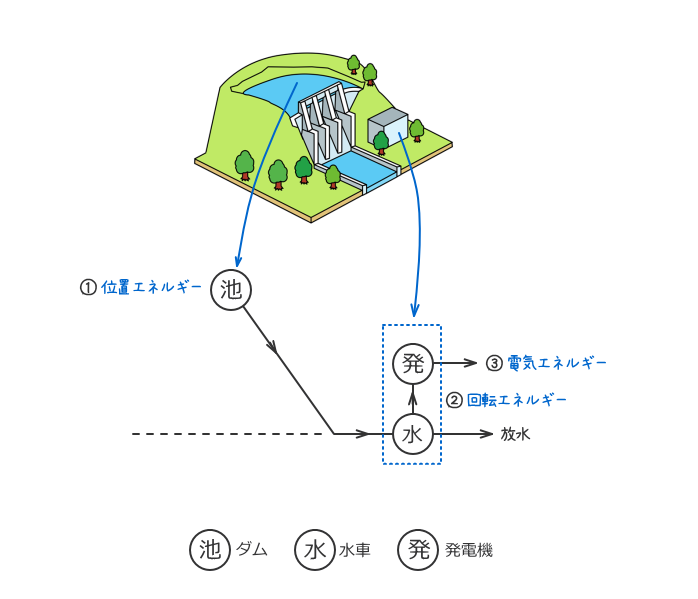
水力発電に限らず、エネルギーの変換を行うときには必ず損失が発生する。
簡単にいうと、①で100のエネルギーがあっても、③では80程度のエネルギーになるので、100－80＝20が損失ということになる。
エネルギー保存の法則から、損失分のエネルギーは無くなってしまうのではなく、取り出せなかっただけで、自然界にエネルギーとして存在している。

 

 

1. 力学の基礎知識

1. 力とは、物体を加速させうる源である。
   

   ---

2. 仕事とは、力によって物体に成し得た評価量である。
   

   ---

3. 仕事率とは、単位時間当たりの仕事である。
   

   ---

4. 力[N]＝質量[kg]×加速度[m/s²]

   ---

5. 仕事[J]＝力[N]×距離[m]

   ---

6. 仕事率[J/s]＝仕事[J]/時間[s]

   ---

7. 電気の仕事率（電力の単位は）は、[W]＝[J/s]を用いる。
   

   ---

8. 高い位置にある物体は、仕事をする潜在的なエネルギー秘めており、これを位置エネルギーと呼んでいる。
   

   ---

9. 地球の表面近くの重力加速度は、g＝9.8[m/s²]である。
   

   ---

10. 基準面から高さH₀[m]にある物体m[kg]に働く力はmg[N]であるので、この物体が保有する位置エネルギーは、mgH₀[J]となる。
    

    ---

11. [kg]の単位は、「キログラム」と読む。
12. [N]の単位は、「ニュートン」と読む。
13. [J]の単位は、「ジュール」と読む。
14. [W]の単位は、「ワット」と読む。
15. ηの記号は、「イータ」と読む。

 

2. 水力発電所の出力公式

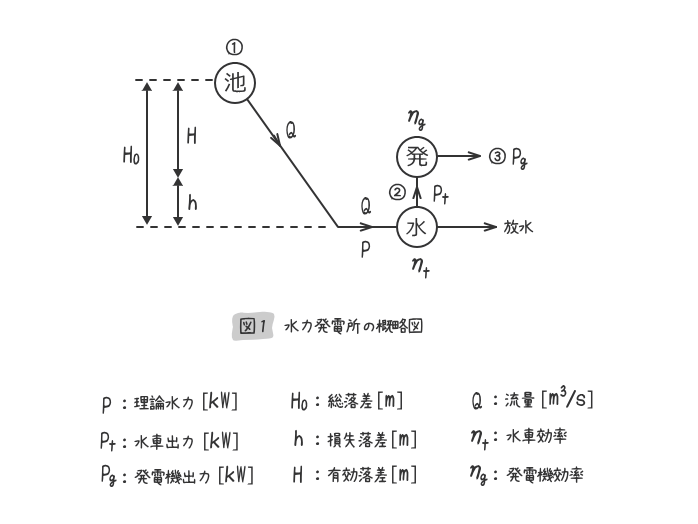
上図1の水力発電所の概略図から、水車への理論水力Pは、下式(1)で表すことができる。
※後述3を参照

水車出力P_tは、上式(1)に水車効率η_tをかければよいので、下式(2)となる。

発電機出力P_g（発電所出力）は、上式(2)に発電機効率η_gをかければよいので、下式(3)となる。

 

3. 理論水力

図1の①で水m[kg]の保有する位置エネルギーは、mgH₀[J]であるが、流水が水車に到達するまでに、水圧管との摩擦によるエネルギー損失が発生する。
損失落差をh[m]とすれば、有効落差は、H＝H₀－h[m]となるので、水車には、mgH[J]のエネルギーを与えることになる。

よって、T秒間にV[m³]の流水を水車に供給する場合の理論水力P[kW]＝P[kJ/s]は、水の密度をρ＝1000[kg/m³]とすれば、下式(4)で表すことができる。

 

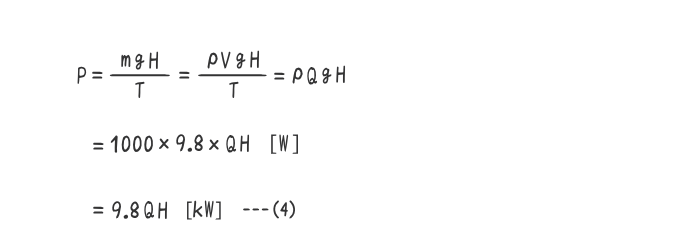
4. 水力発電所の動画（YouTubeより引用）

 

例題

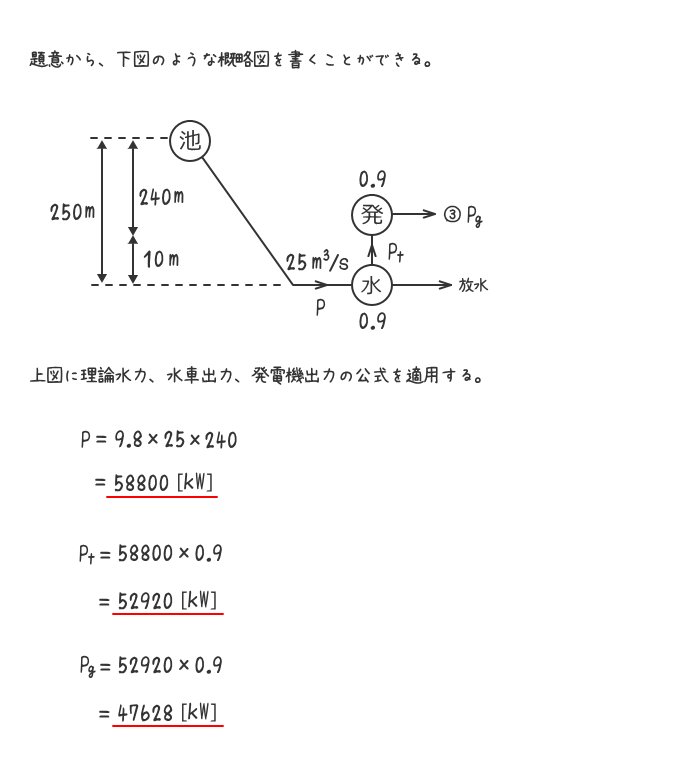
総落差250[m]、損失落差10[m]の水力発電所がある。
この発電所の使用流量を25[m³/s]とした場合の理論水力[kW]、水車出力[kW]、発電機出力[kW]を求めよ。
ただし、水車効率と発電機効率は共に90[%]であるものとする。