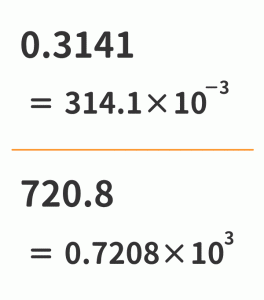ベクトル
私達の周囲には矢印があふれており、向き(方向)を示す図記号として広く活用されている。

数学で用いるベクトルと呼ばれている矢印は、向きと大きさを併せ持つ量として考える。
矢印の太さで大きさを強調するのではなく、長さで大きさを強調する。
目次
1. ベクトルの基本事項
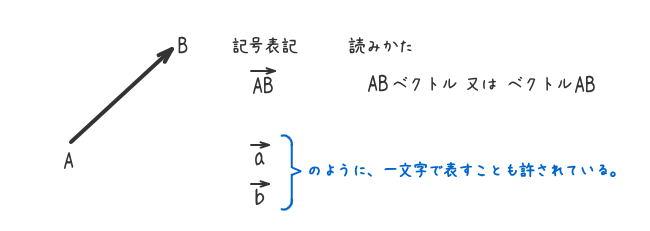
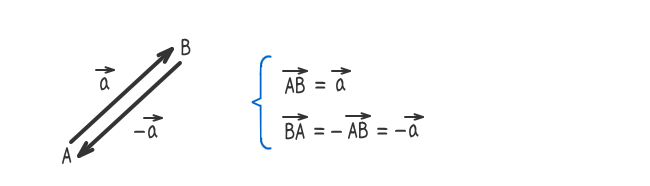
- Aをベクトルの始点、Bをベクトルの終点という。

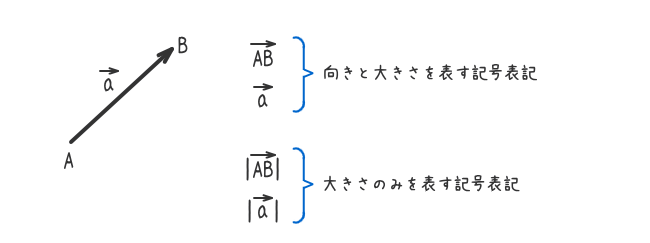
- ベクトルの記号表記と読みかた。
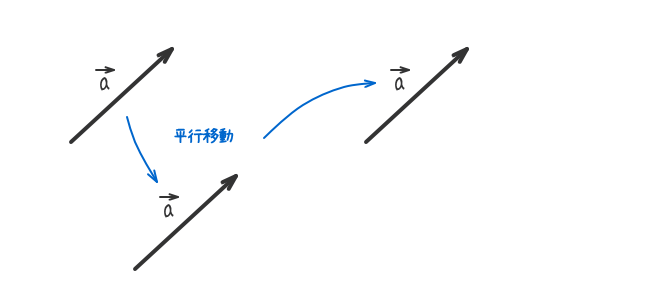
- 等しいベクトルとは、向きと大きさが同じベクトルである。ベクトルがある位置は無関係である。
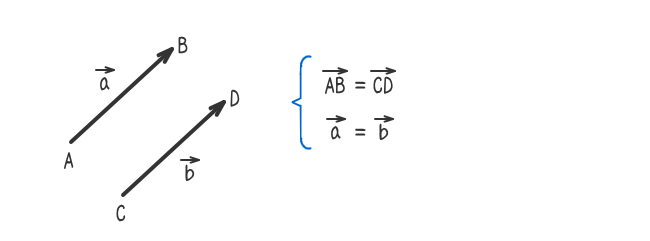
- 上述3から、ベクトルは自由に平行移動させることができる。
- ベクトルABと大きさが等しくて、向きが反対のベクトルをベクトルABの逆ベクトルという。
- ベクトルの大きさのみを表す記号表記
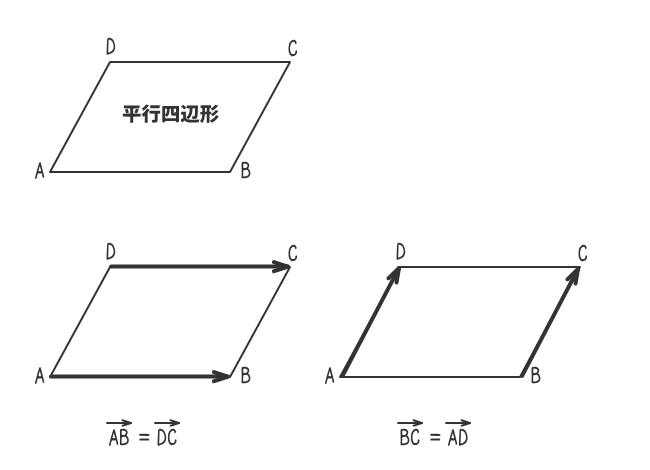
- 平行四辺形ABCDのベクトルABとベクトルDCは等しい。
平行四辺形ABCDのベクトルADとベクトルBCは等しい。
2. ベクトルの加法
二つのベクトルの和を一つのベクトルで表す。
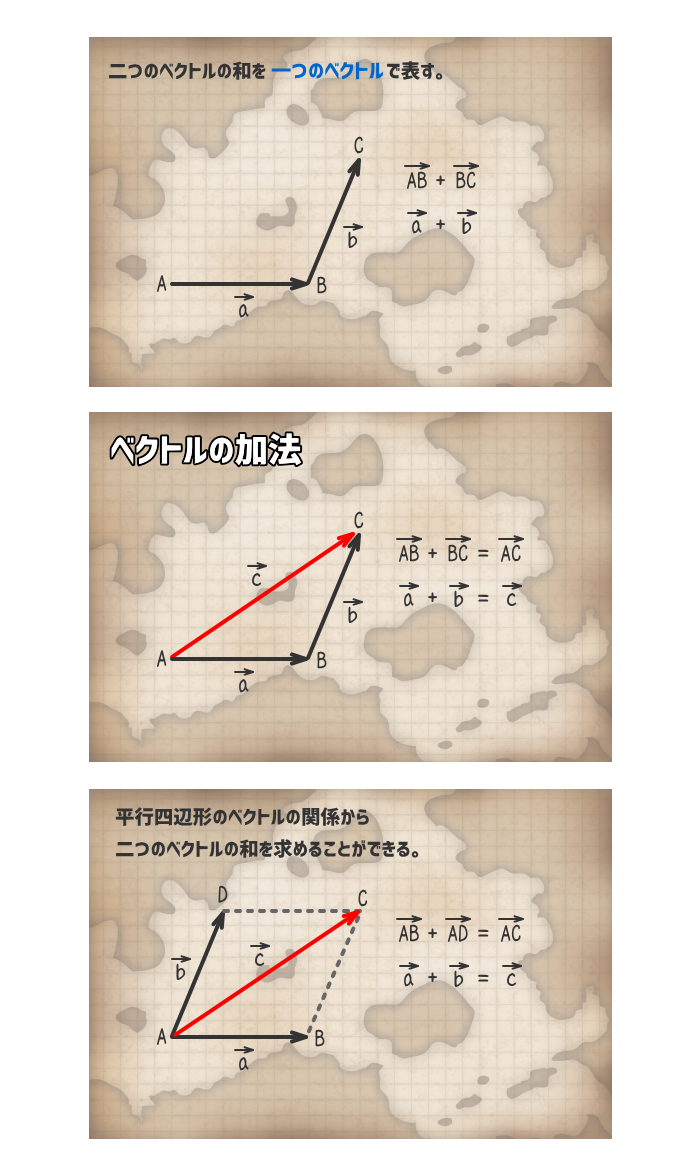
3. ベクトルの減法
二つのベクトルの差を一つのベクトルで表す。

4. ベクトルの実数倍
ベクトルを実数倍すると、ベクトルの長さが拡大・縮小したり、向き反対になることがある。
ただし、零ベクトルの実数倍は、零ベクトルである。
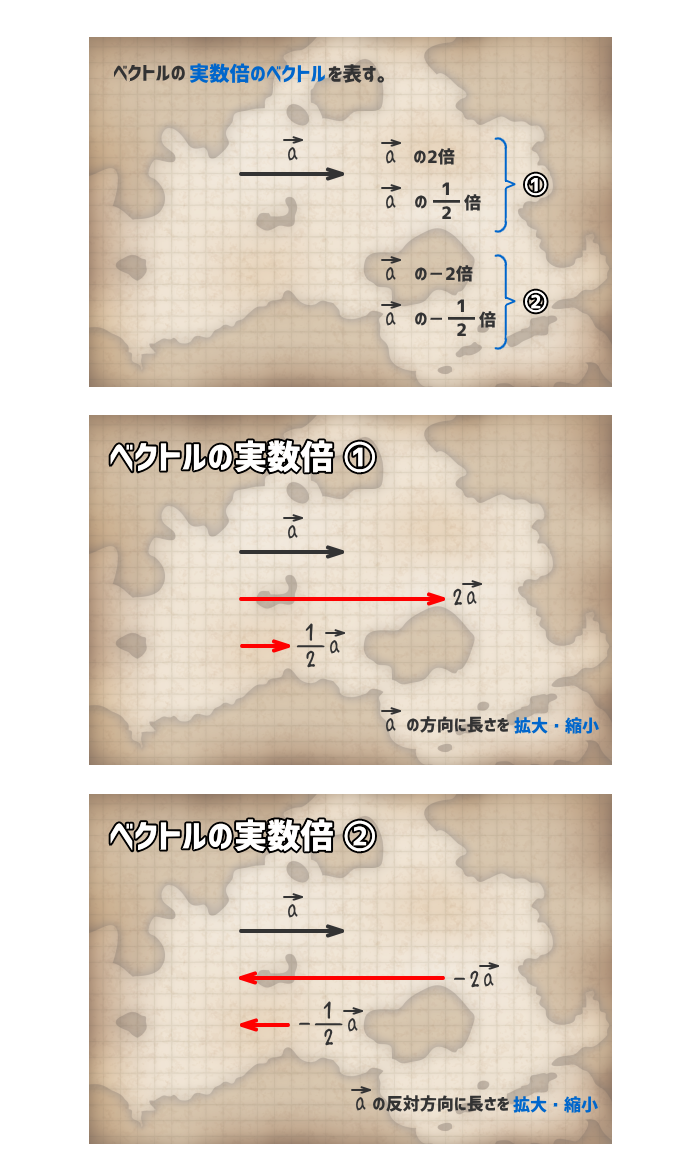
5. ベクトルの分解
一つのベクトルは、二つ以上のベクトルに分解することができる。

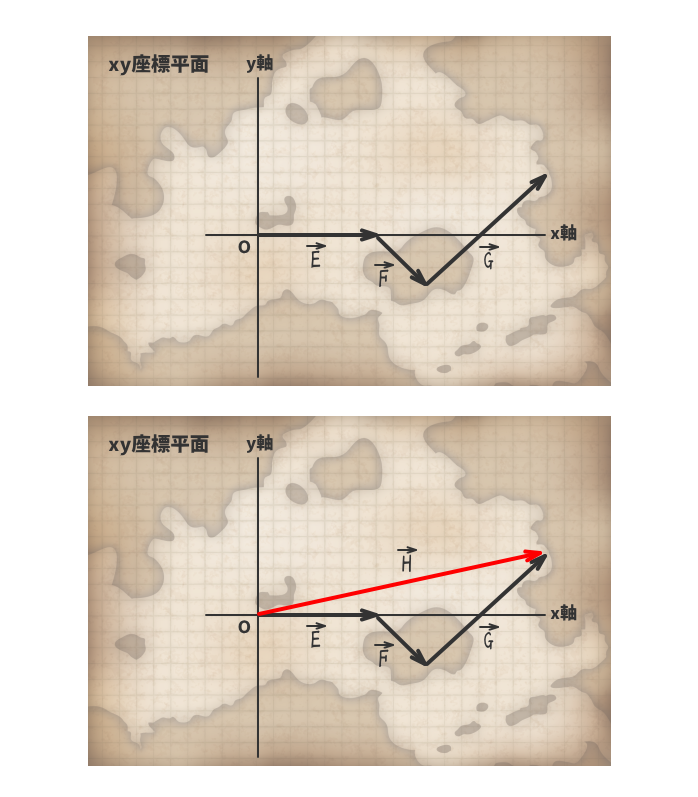
6. ベクトルとxy座標平面
地図上に座標平面を自由に設定することができる。
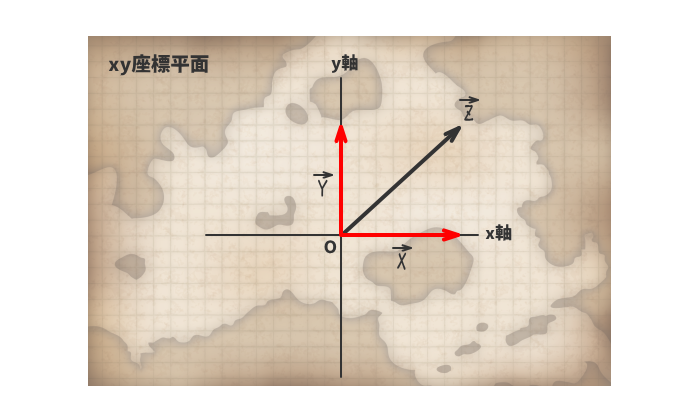
ベクトルZの始点を座標平面の原点Oに合わせて、座標軸上にベクトルを分解する。
ベクトルE+ベクトルF+ベクトルG=ベクトルH
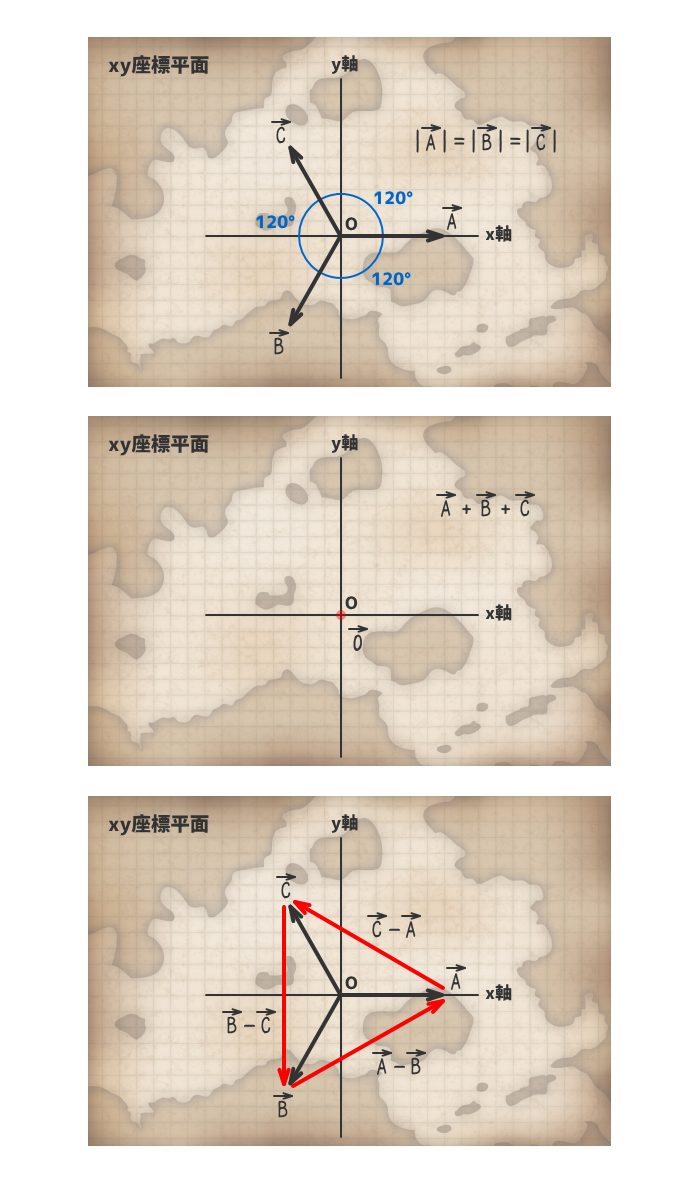
ベクトルA+ベクトルB+ベクトルC
ベクトルA-ベクトルB
ベクトルB-ベクトルC
ベクトルC-ベクトルA
7. 基本ベクトルとxy座標平面
原点Oからx軸又はy軸の正方向の向きを持つ大きさが1のベクトルを基本ベクトルという。

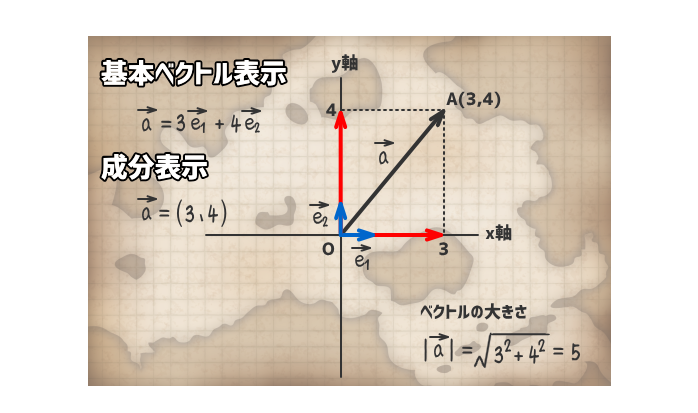
8. 基本ベクトル表示と成分表示
原点Oを始点とし、終点が点AのベクトルOAをx軸とy軸上に分解すると、点Aの座標と基本ベクトルを用いて、ベクトルOAを表現することができる。
このときのx座標をベクトルOAのx成分、y座標をベクトルOAのy成分という。
また、ピタゴラスの定理(三平方の定理)からベクトルOAの大きさを成分で示すことができる。
例題1
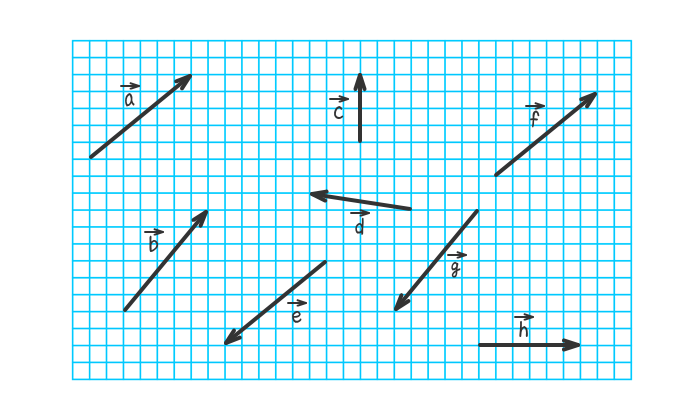
下図のベクトルaと等しいベクトルと逆ベクトルのものはどれか選びなさい。
解答を表示する

解答を非表示にする
例題2
下図のベクトルa+ベクトルb、ベクトルc+ベクトルd、ベクトルe+ベクトルfを図示しなさい。

解答を表示する
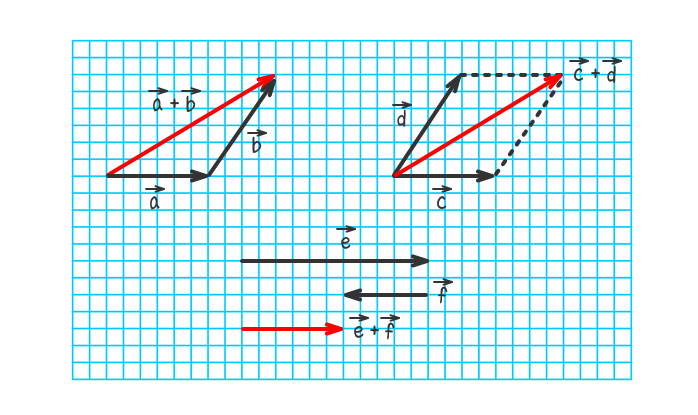
解答を非表示にする
例題3
下図のベクトルa-ベクトルb、ベクトルc-ベクトルd、ベクトルe-ベクトルfを図示しなさい。
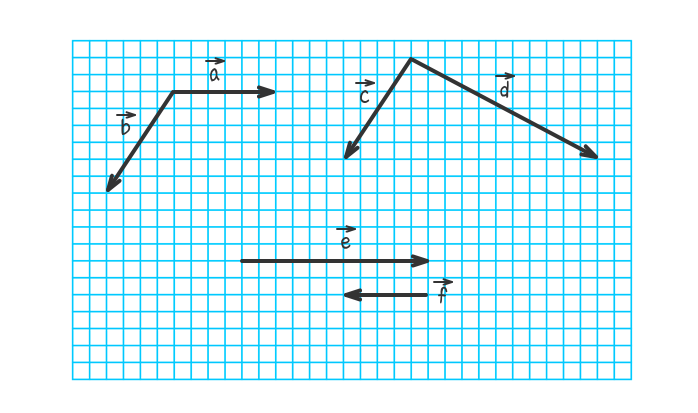
解答を表示する
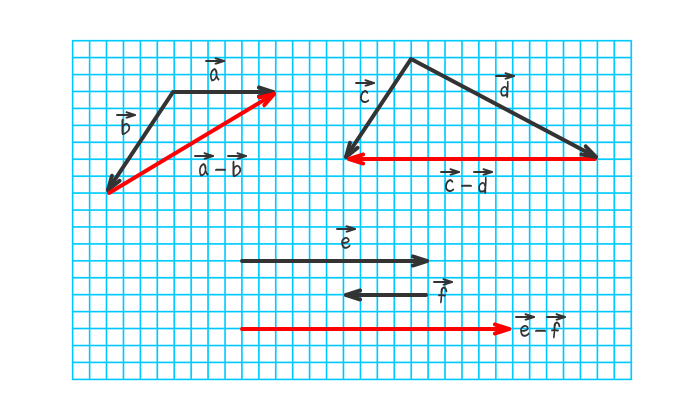
解答を非表示にする
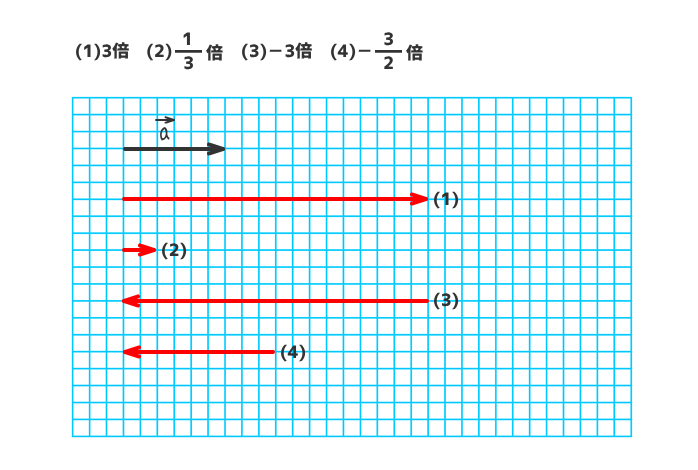
例題4
下図のベクトルaについて、(1)~(4)の実数倍の結果を図示しなさい。
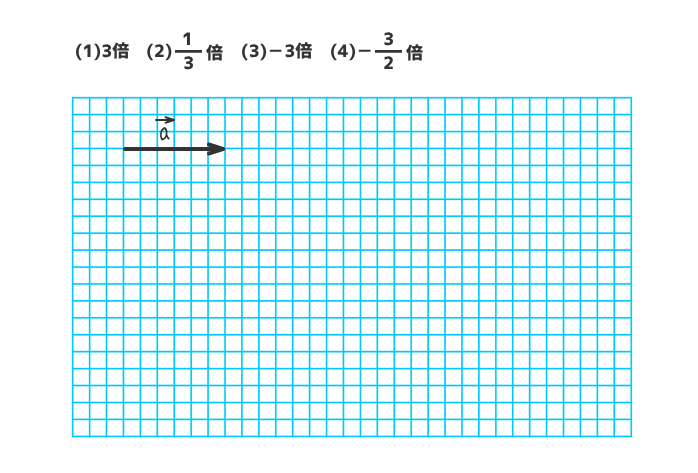
解答を表示する
解答を非表示にする
例題5
ベクトルの和と差と実数倍の結果を念頭に置いて、次の(1)~(5)のベクトルの計算を文字式と同様に考えて行いなさい。
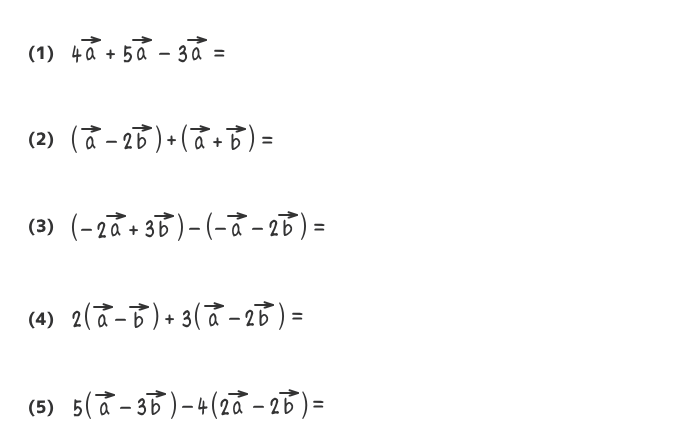
解答を表示する

解答を非表示にする
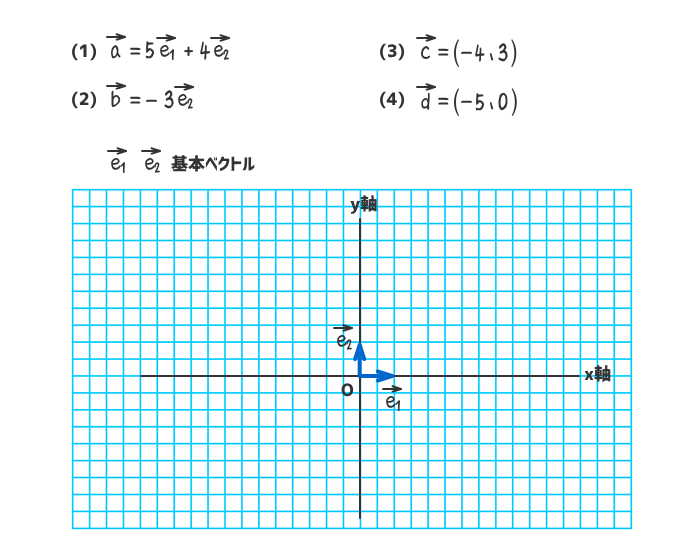
例題6
次の(1)と(2)の基本ベクトル表示と(3)と(4)の成分表示のベクトルを図示しなさい。
解答を表示する

解答を非表示にする
例題7
次の(1)から(4)のベクトルの大きさを求めなさい。

解答を表示する
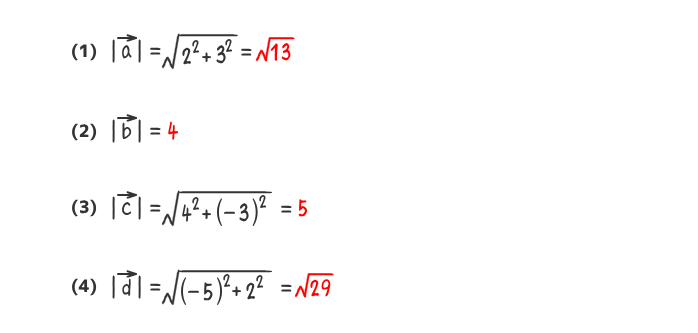
解答を非表示にする