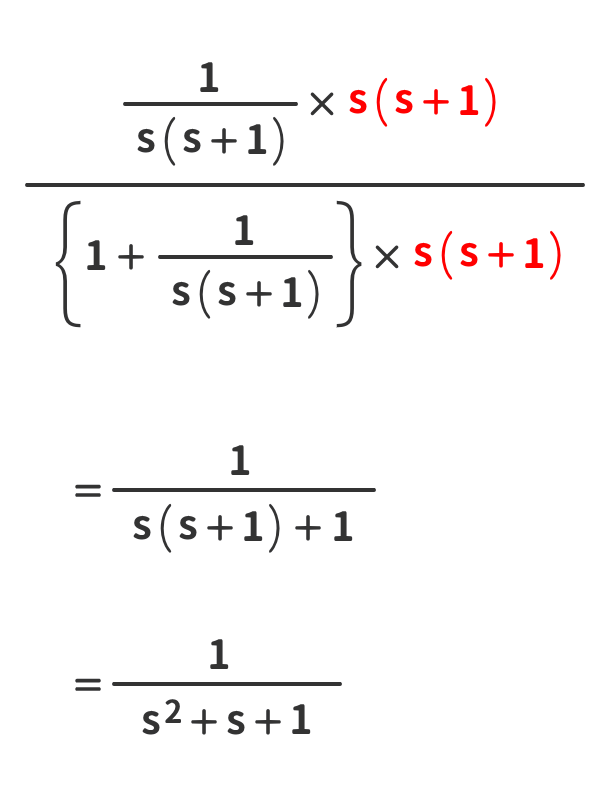「繁分数式」の簡単化をしよう!
電験三種の計算問題では、「繁分数式の計算」が頻繁に登場する。
この記事の目的は、中学生・高校生のときに学んだ繁分数式なる得体のしれないものと「仲良く」なってもらうことである。
言い換えると「繁分数式はこわくない!」と思ってもらうための記事です。
この記事は「分数計算の記憶を引き出そう!」の内容を拡張したものです。

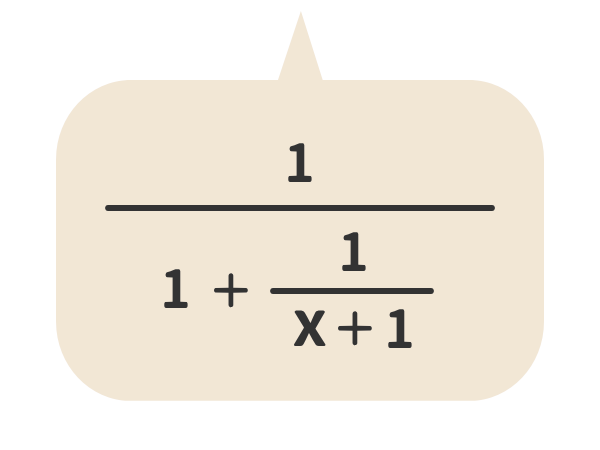
繁分数式の簡単化のための準備
ここでは繁分数式と仲良くなるための準備を行うものとする。
準備[1]
数学では、「数字や数式」を「文字」で置き換えることを頻繁に行っている。
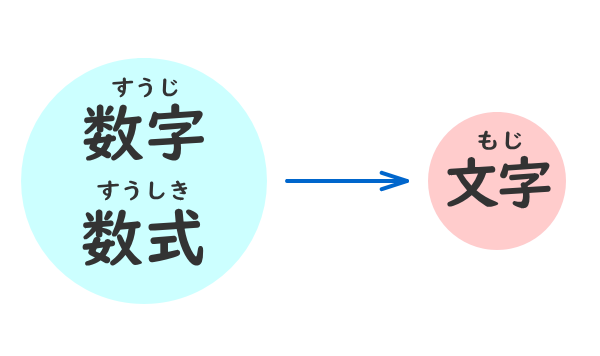
例①
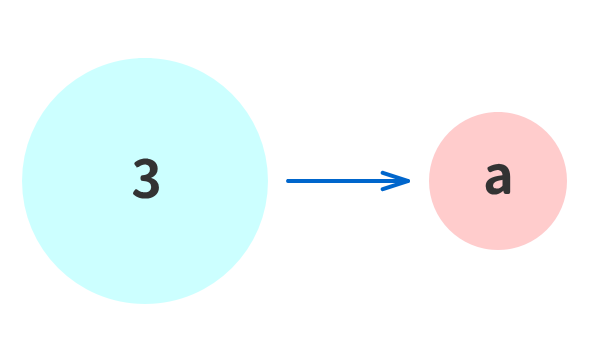
例②
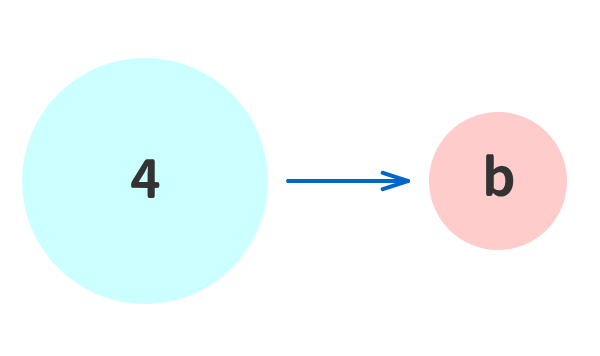
例③
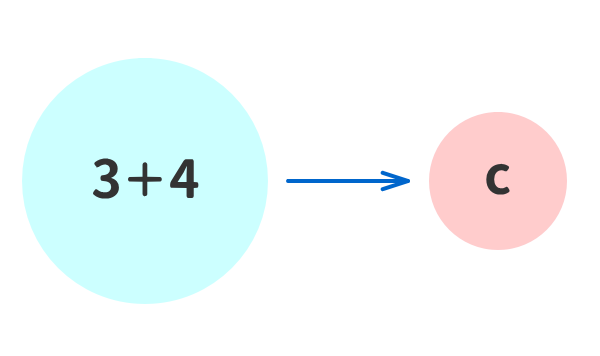
例④
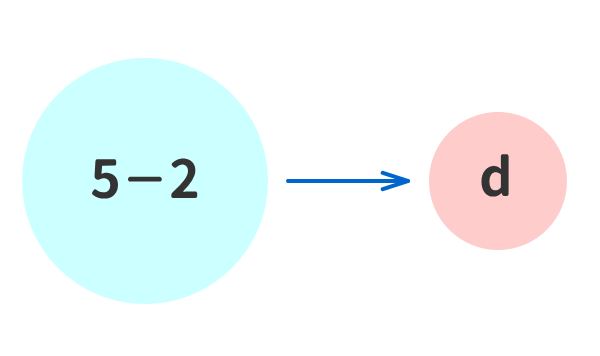
例⑤
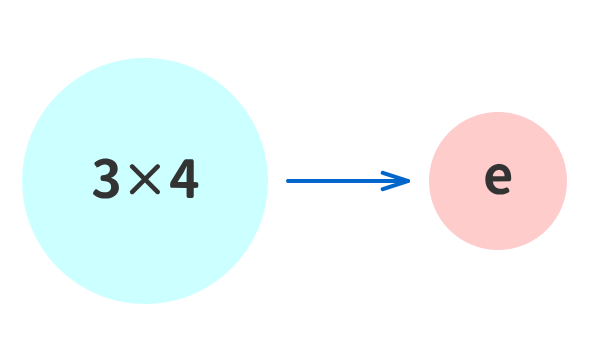
例⑥
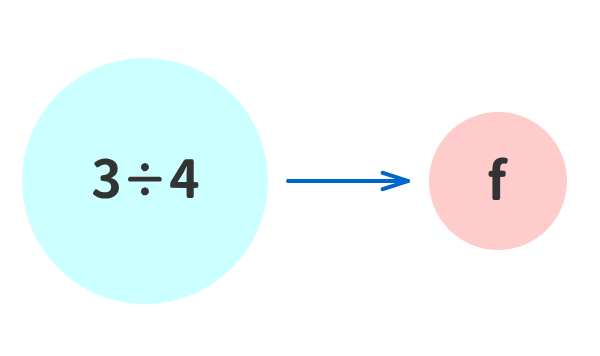
例⑦

準備[2]
さらに数学では、「数字と文字で表されてる数式(文字式という)」を「文字」で置き換えることもある。
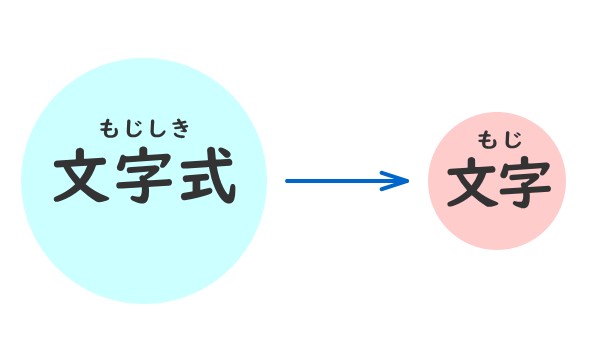
例①
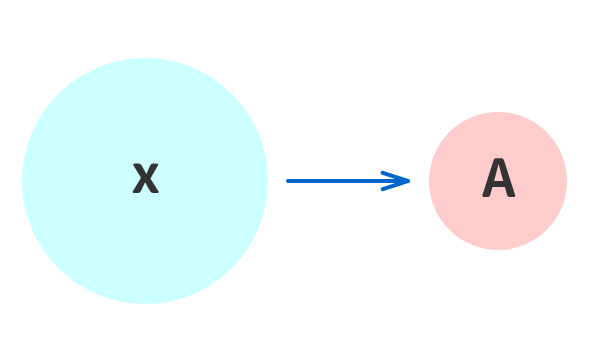
例②
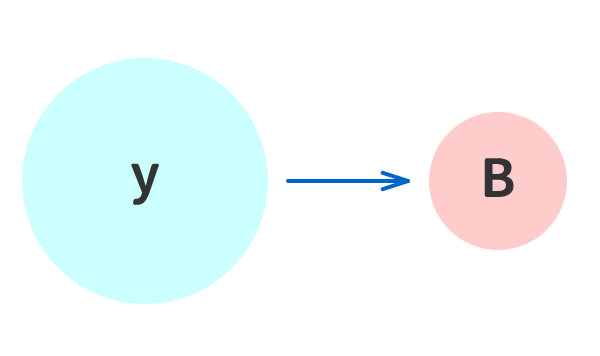
例③
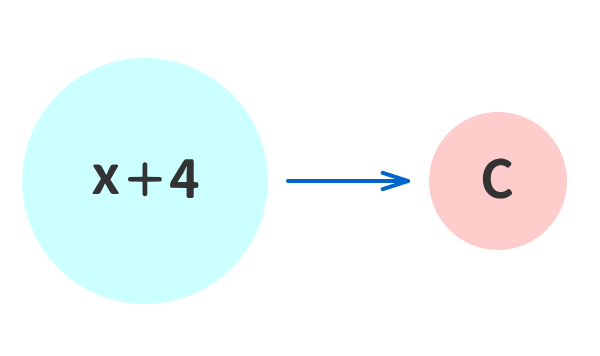
例④
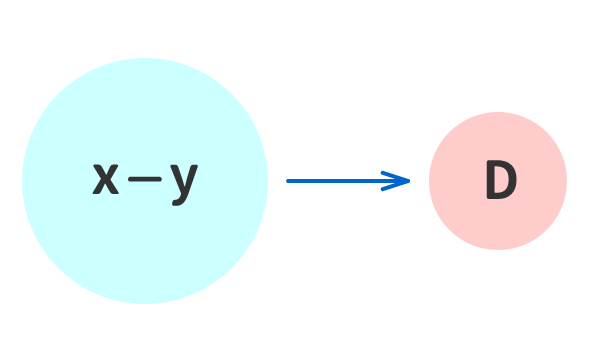
例⑤
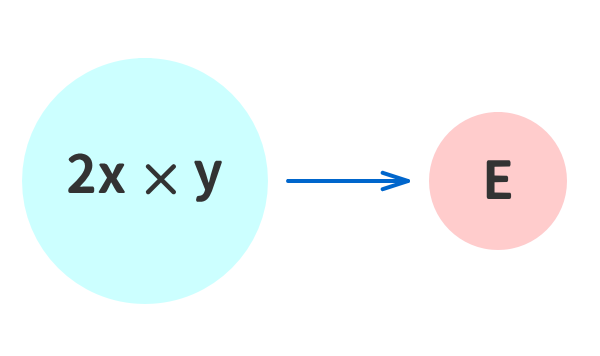
例⑥
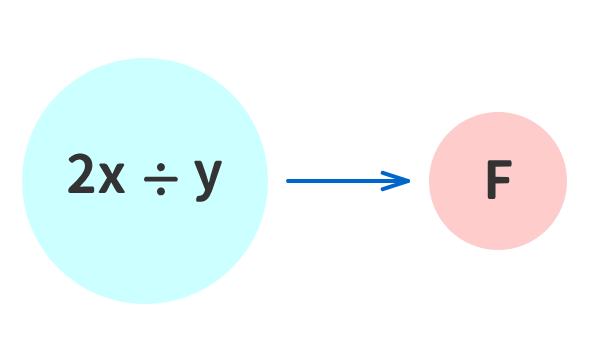
例⑦

準備[3]
下図の「二段弁当」により「分数式」のイメージをつかもう。
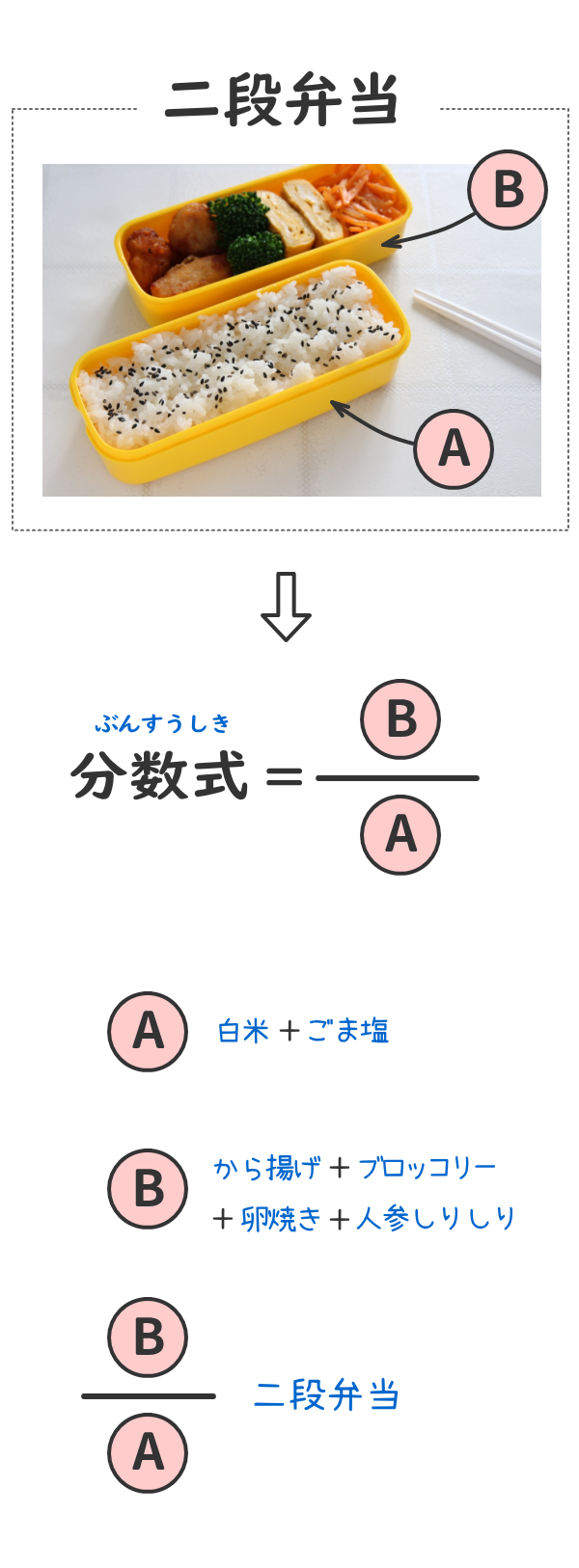
準備[4]
下記の例に示すような分数形式の文字が含まれている数式を「分数式」という。
例①
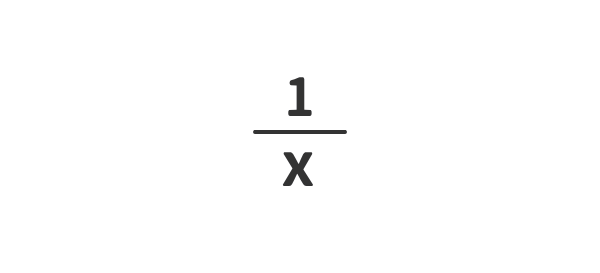
例②

例③
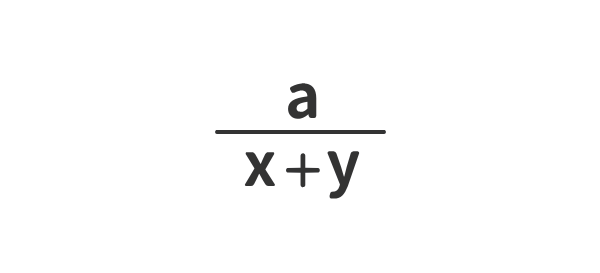
例④
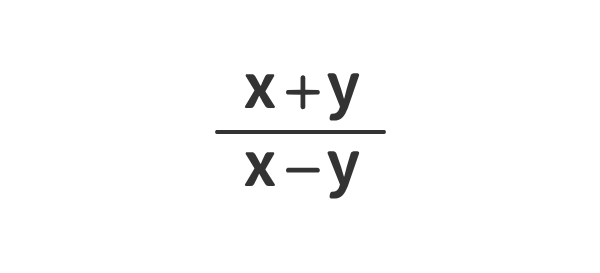
例⑤
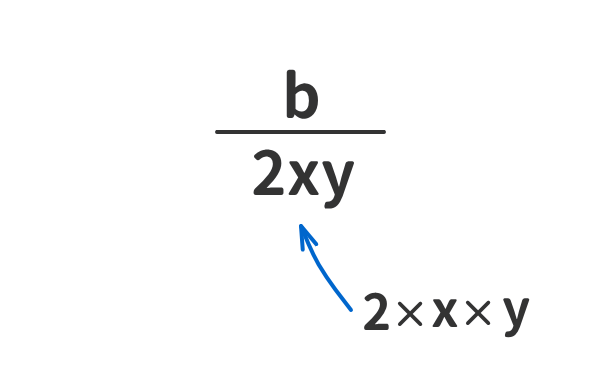
例⑥
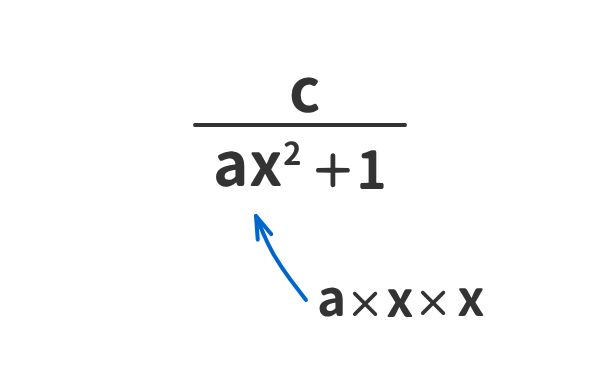
準備[5]
下記の例に示すように、分数式の分母と分子を文字A、B、C、D、E、F、G、H、I、J、Kの「ひと塊」と見立てることができる。
準備[3]の「二段弁当のイメージ」を思い出そう!
Aという「ひと塊」を認識。
その中身は「白米+ごま塩」!
Bという「ひと塊」を認識。
その中身は「唐揚げ+ブロッコリー+卵焼き+人参しりしり」
A分のBという「ひと塊」の二段弁当を認識。

場合によっては、Aという「ひと塊」を認識しても、その中身が「白米」だけのこともあるかもしれない。
例①

例②
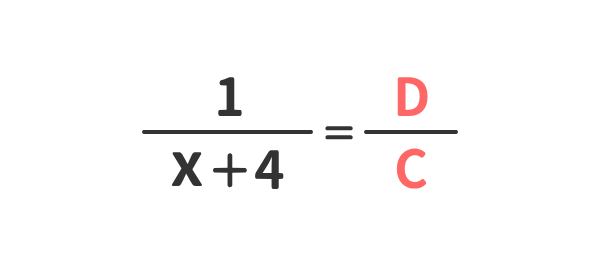
例③
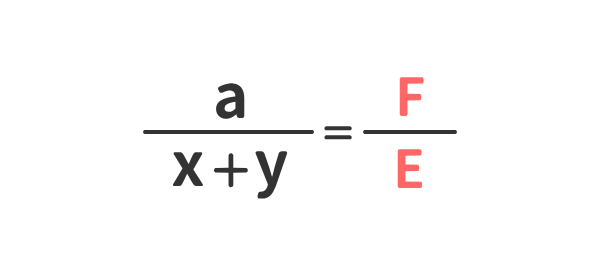
例④

例⑤
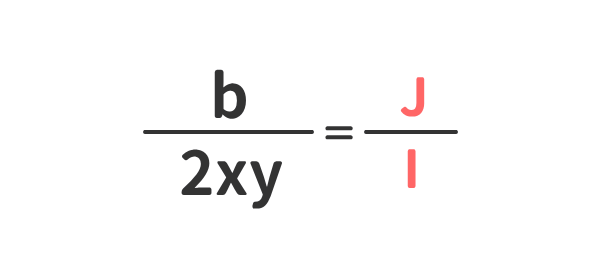
例⑥
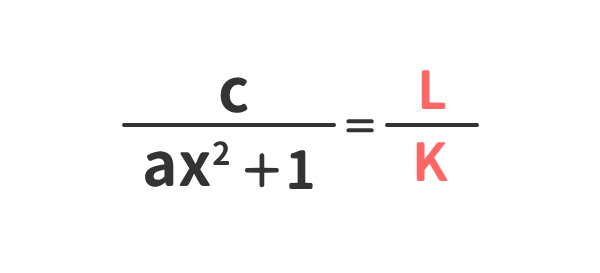
準備[6]
「分数式のかけ算とわり算」は「分数のかけ算とわり算」と同じである。
「分数」のかけ算の例
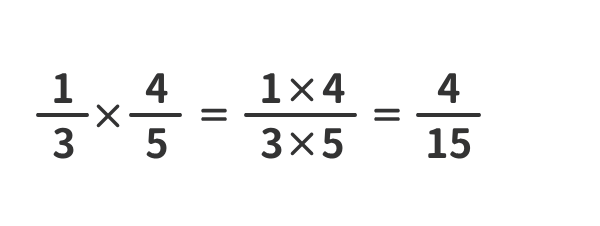
「分数」のわり算の例
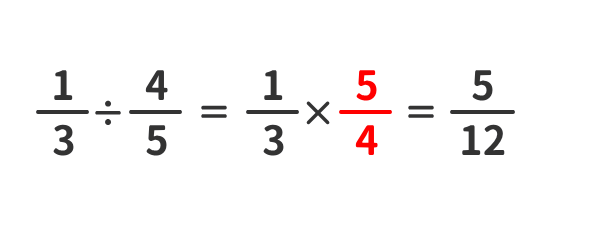
「分数式」のかけ算の例
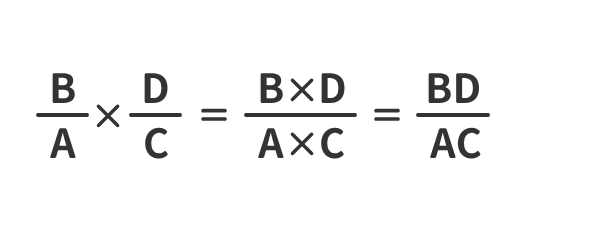
「分数式」のわり算の例
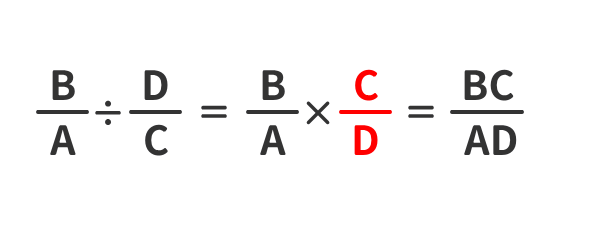
準備[7]
「ある分数式」と「ある分数式の逆数」のかけ算は「1」になる。
これは、分数の場合と一緒である。
「分数」の例
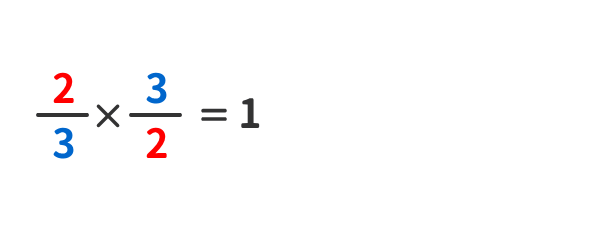
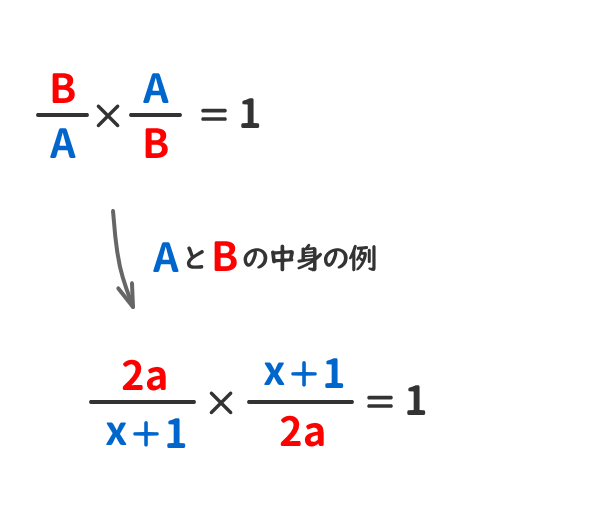
「分数式」の例
準備[8]
「分数式の通分」も「分数の通分」と一緒である。
「分数」の例
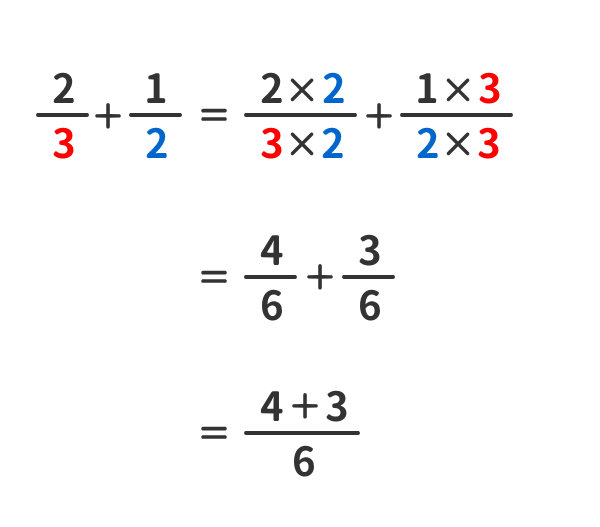
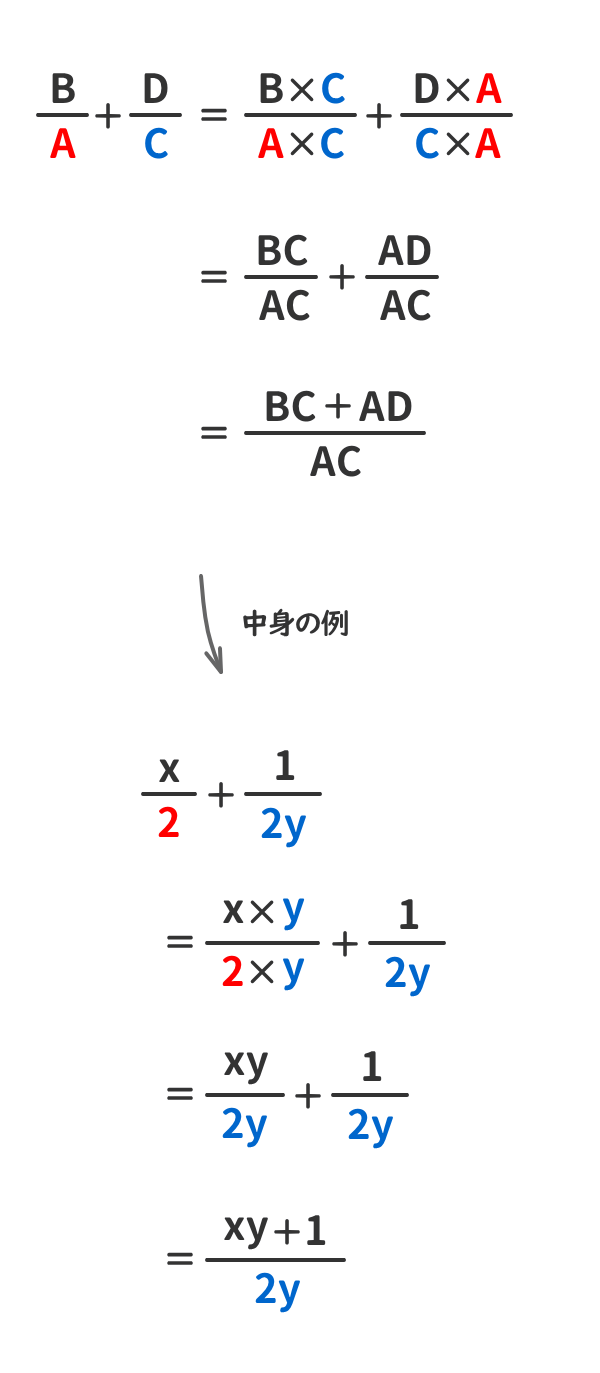
「分数式」の例
準備[9]
「ひと塊」を利用すると、括弧を外す「式の展開」が分かりやすくなるよ。
「展開公式」を忘れても、この見方ができれば括弧を外せる。
例① (x+1)(x+2)
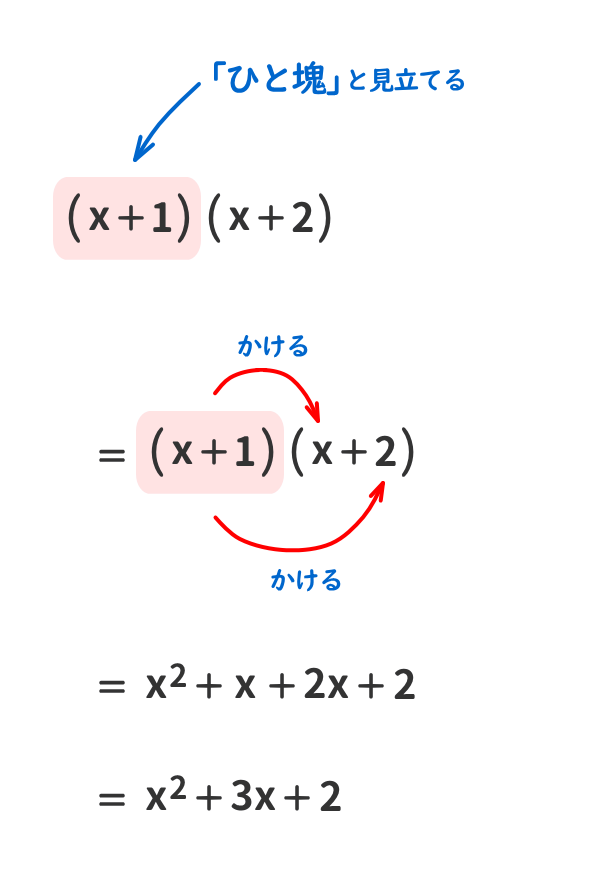
例② (x-3)(x+2)

繁分数式の簡単化をしよう!
分数式の分母または分子に、分数式が含まれている分数式を繁分数式「はんぶんすうしき」という。
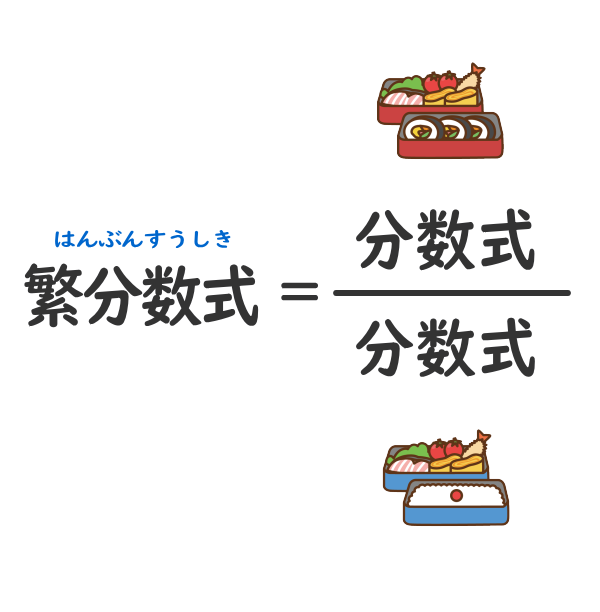
繁分数式のままだと「繁雑」で式の意味が良くわからない。
ゆえに「繁雑な状況」を解消して簡単な分数式で表す必要がある。
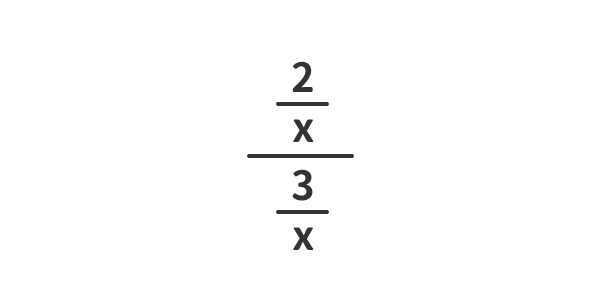
繁分数式を簡単にする方法は、分母と分子に同じ数(同じ数字、同じ文字、同じ式)をかけることである。
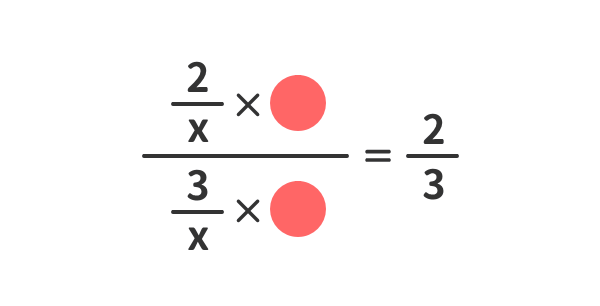
繁分数を簡単化する例(1)
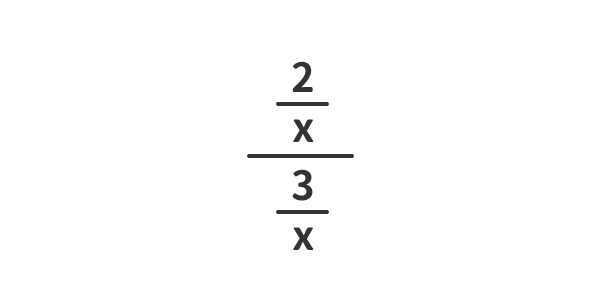
式の見立て
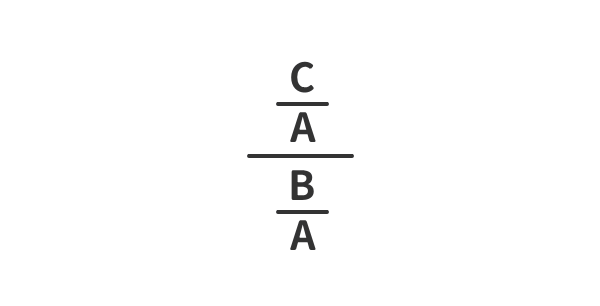
簡単化①
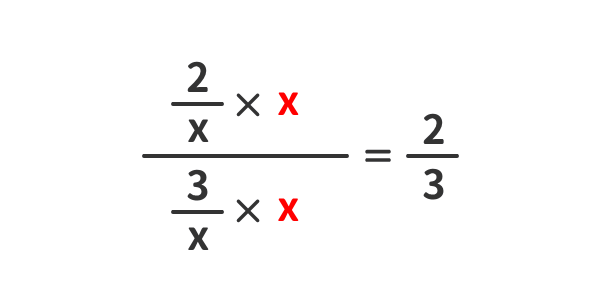
簡単化②
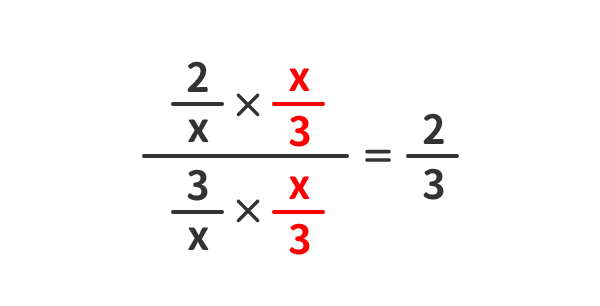
繁分数を簡単化する例(2)
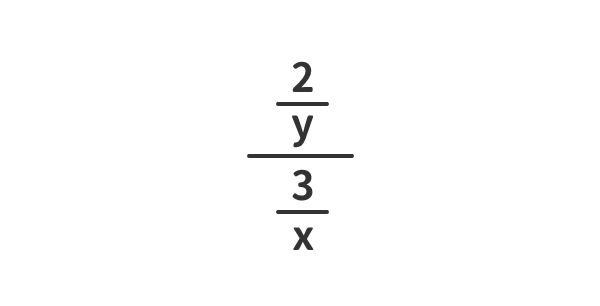
式の見立て
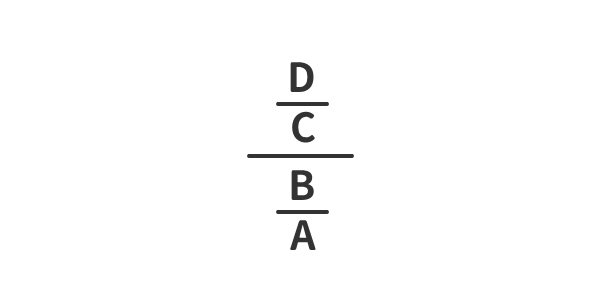
簡単化①

簡単化②
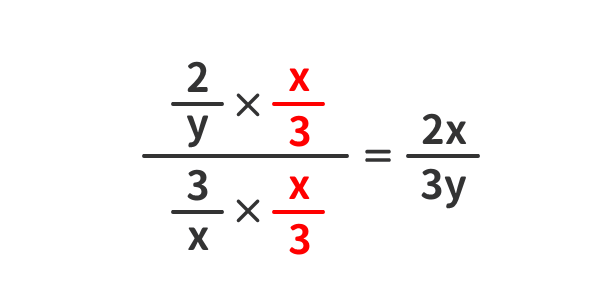
繁分数を簡単化する例(3)
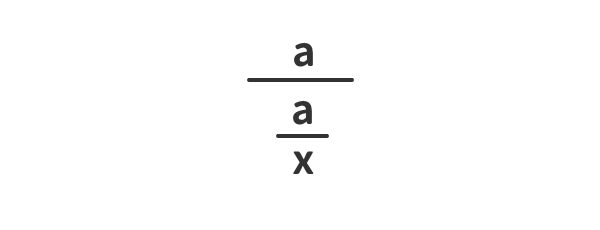
式の見立て
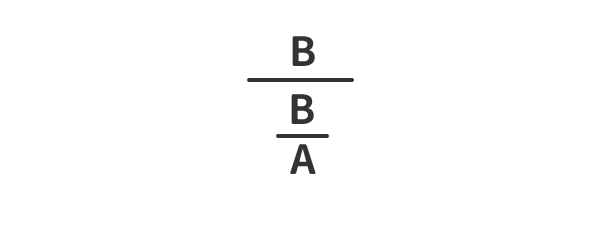
簡単化①
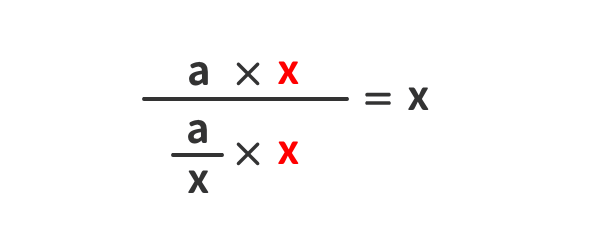
簡単化②
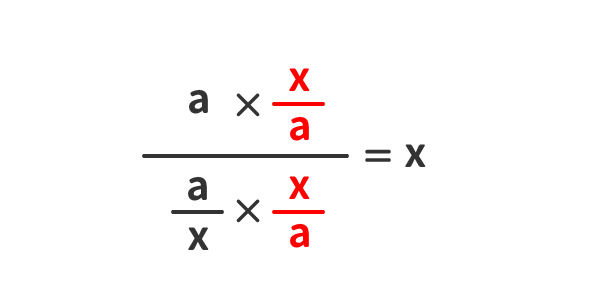
繁分数を簡単化する例(4)
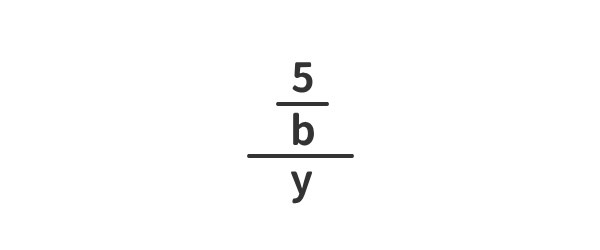
式の見立て
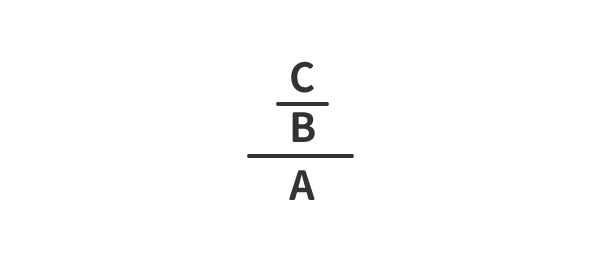
簡単化①
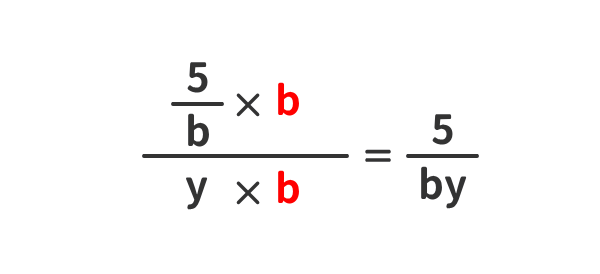
簡単化②
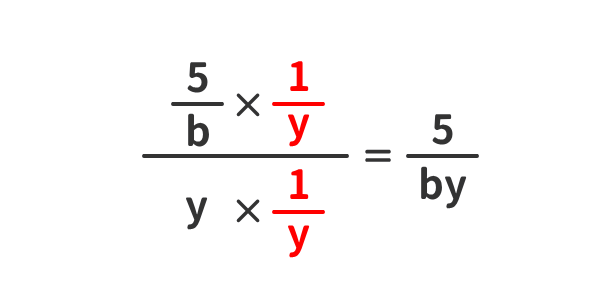
繁分数を簡単化する例(5)
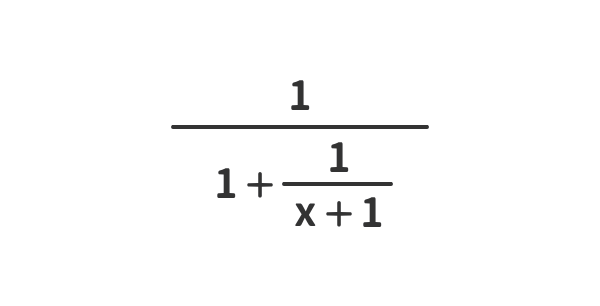
式の見立て

簡単化①
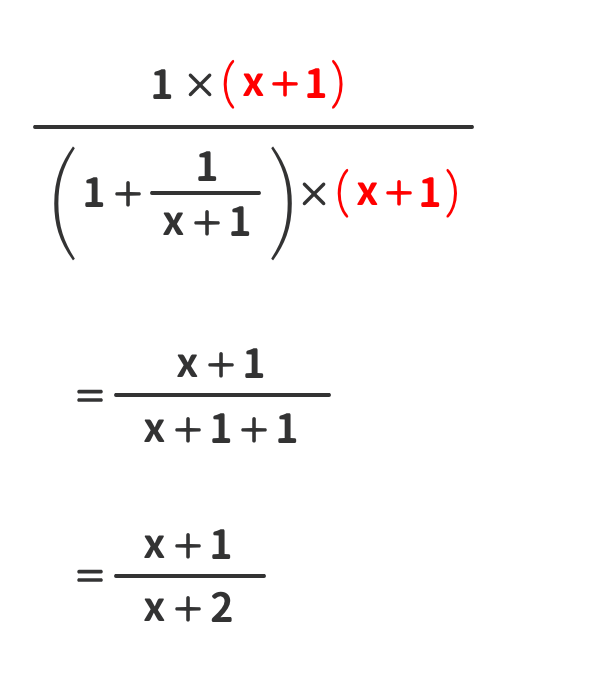
簡単化②
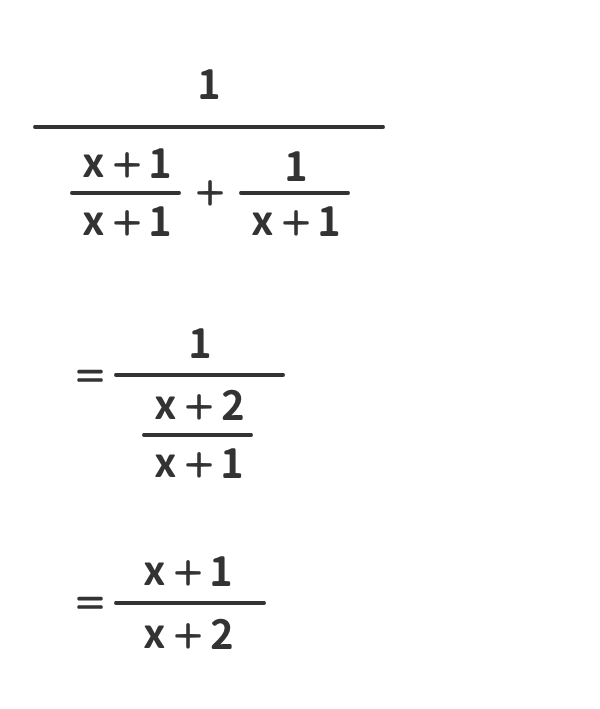
繁分数を簡単化する例(6)
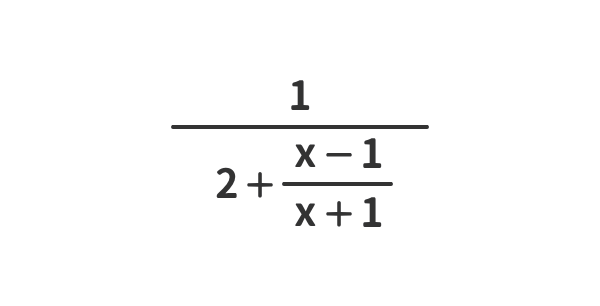
式の見立て
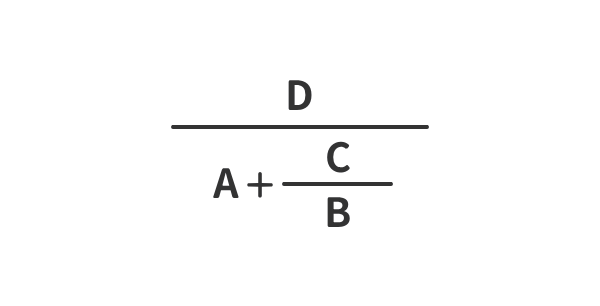
簡単化①
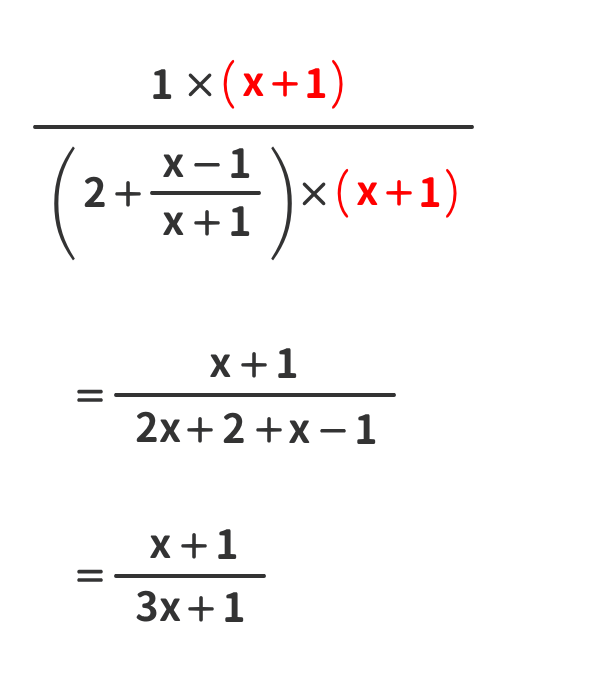
簡単化②
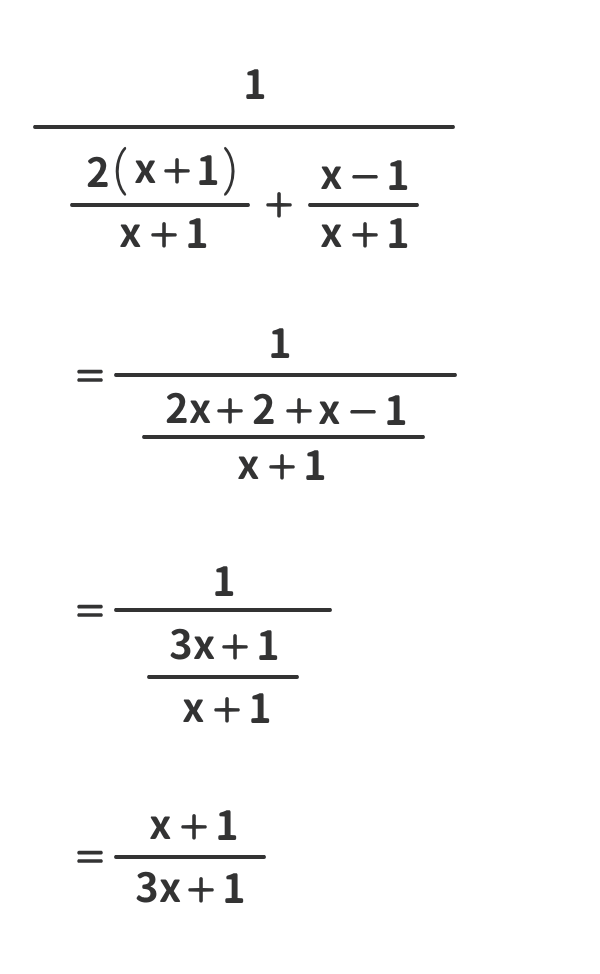
繁分数を簡単化する例(7)
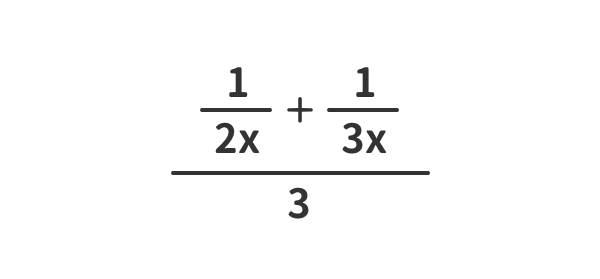
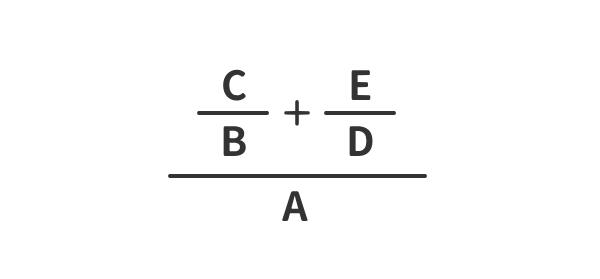
式の見立て
簡単化①
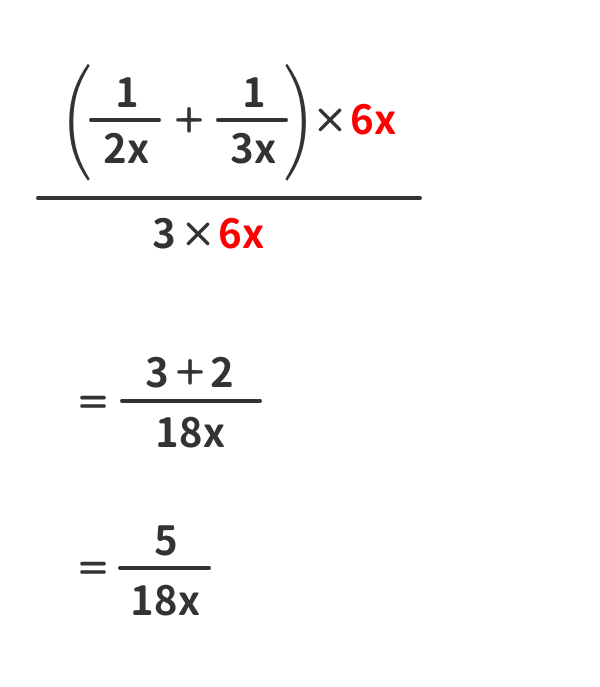
簡単化②
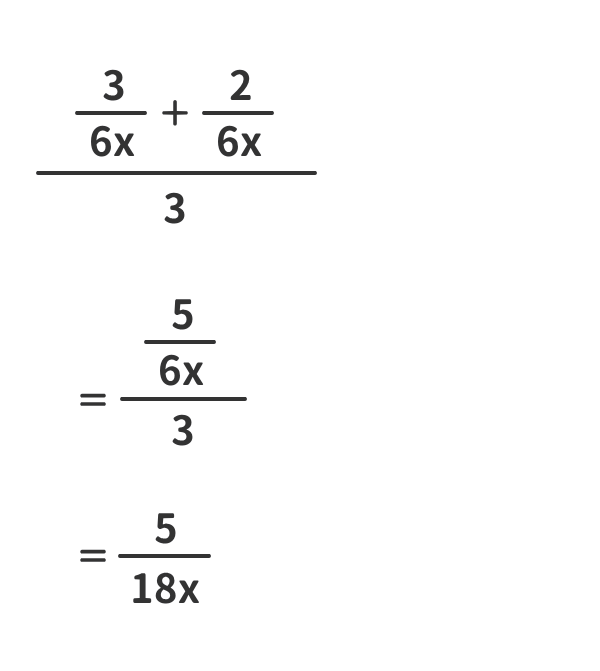
繁分数を簡単化する例(8)
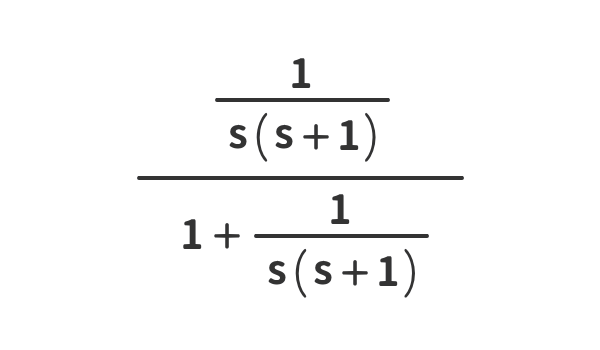
式の見立て
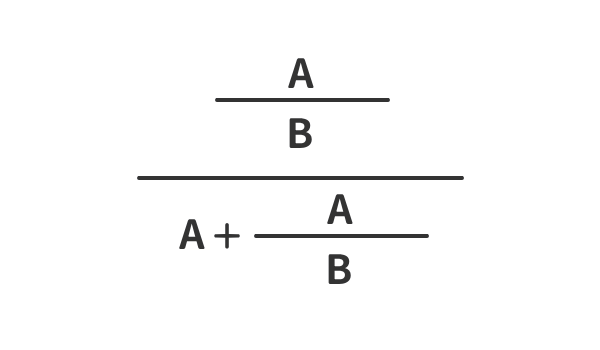
簡単化①