オームの法則
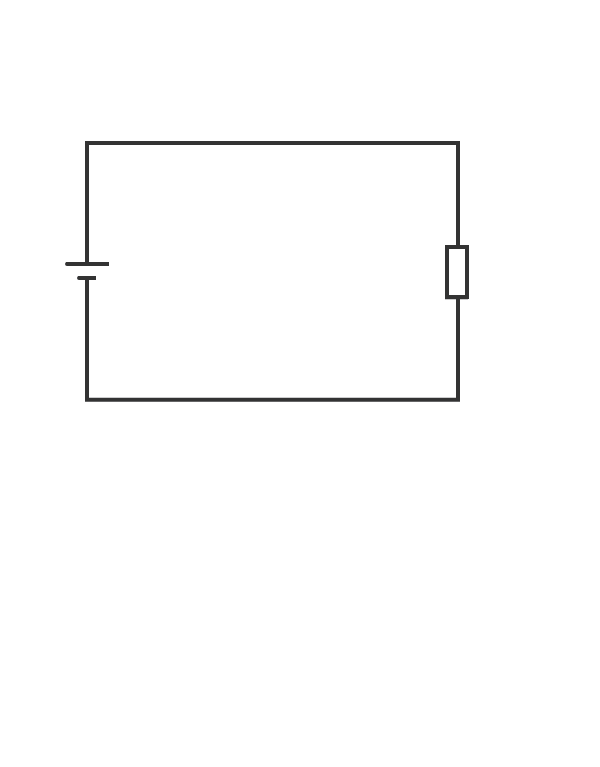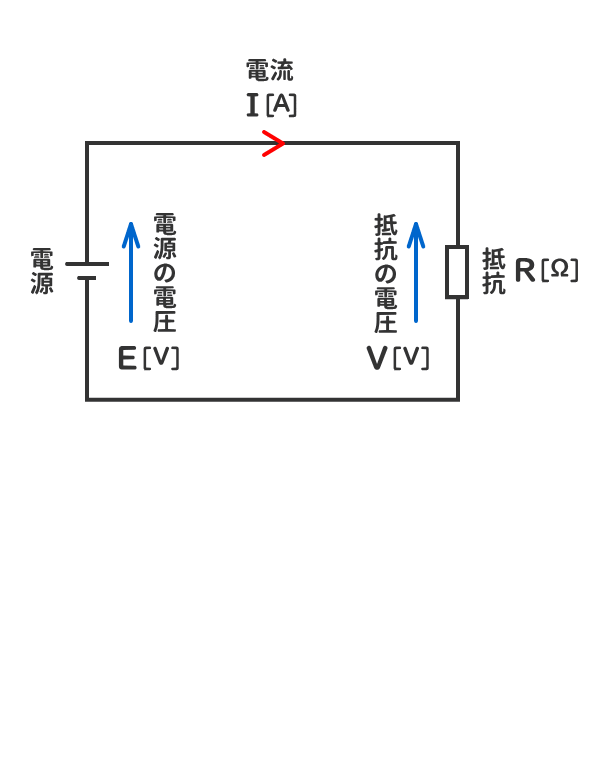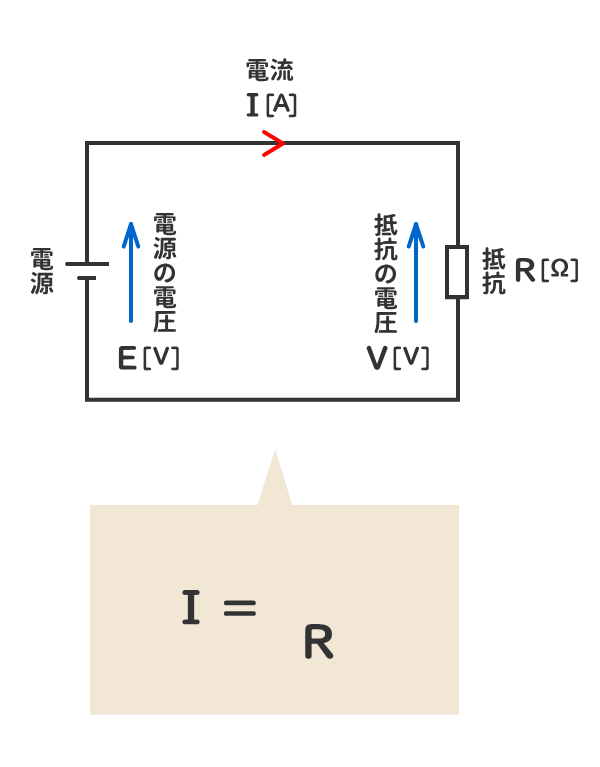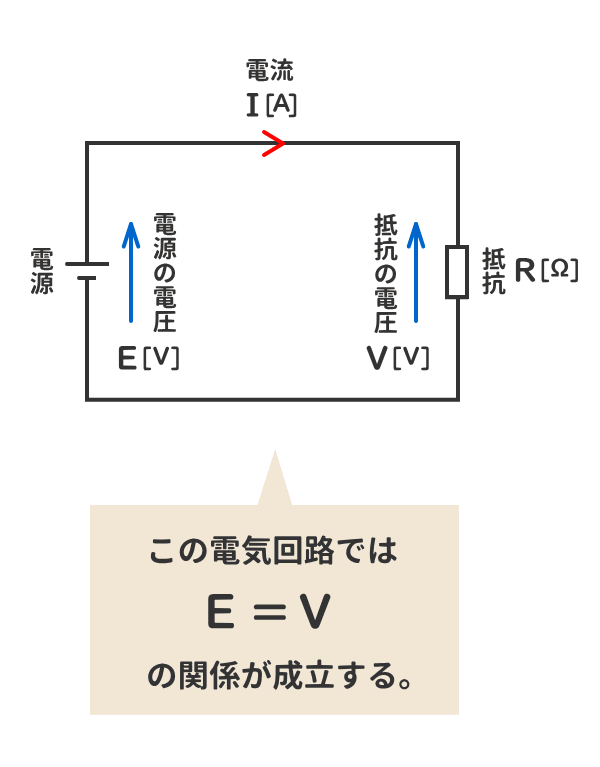
オームの法則とは、電気回路における電圧、電流、抵抗の関係を示した法則である。
オームの法則は、目には見えない電気回路の現象を簡単に説明するのに成功した法則である。
目次
- 電気回路の基礎知識
- 1. 抵抗が二つある場合のオームの法則
- 2. 当該の電気回路の抵抗の電圧の和は、電源の電圧と同じになる。
- 3. 電源の電圧はスイッチがOFFでも発生しているが、抵抗には電流が流れていないので、抵抗の電圧は発生しない。
- 4. 抵抗の電圧は、スイッチをONして抵抗に電流が流れることによって発生する。
- 5.電源の電圧と抵抗の電圧を区別するために、電源の電圧を「起電力」、抵抗の電圧を「電圧降下」と呼称することがある。
- 6.電流は、分流しても合流しても失われない。
- 7.並列箇所に加わる電圧は同じである。
- 8.抵抗を直線上に接続することを「抵抗の直列接続」という。
- 9.抵抗を並べて接続することを「抵抗の並列接続」という。
- 例題1
- 例題2
- 例題3
- 例題4
- 例題5
- 例題6
- 関連事項ピックアップ
- 関連記事
電気回路の基礎知識
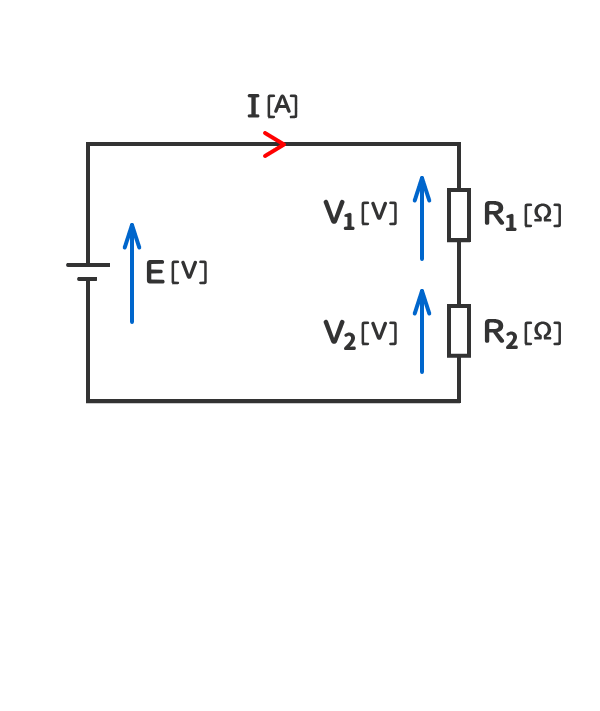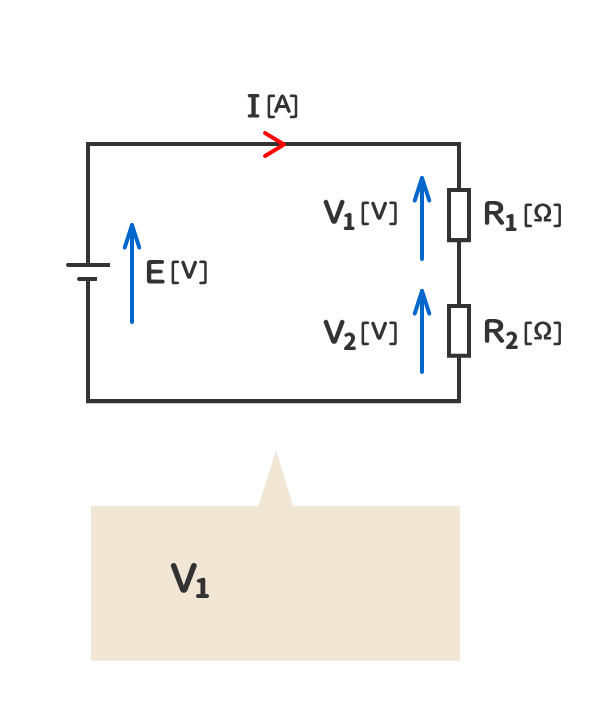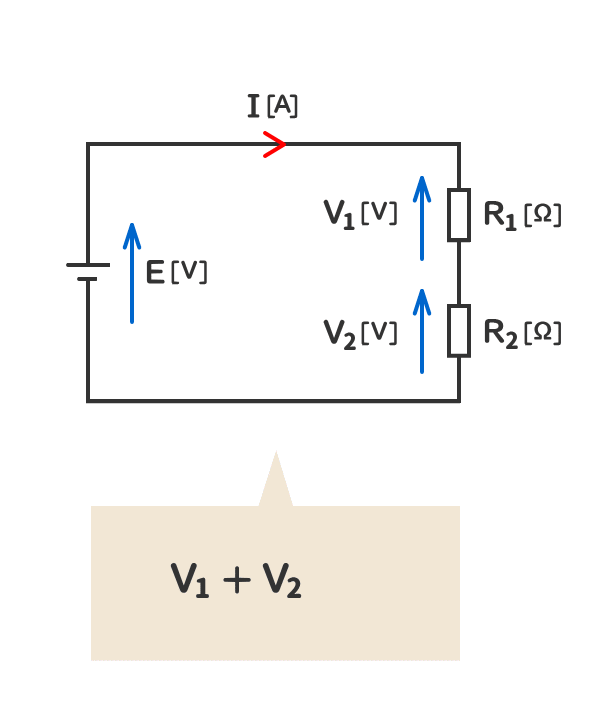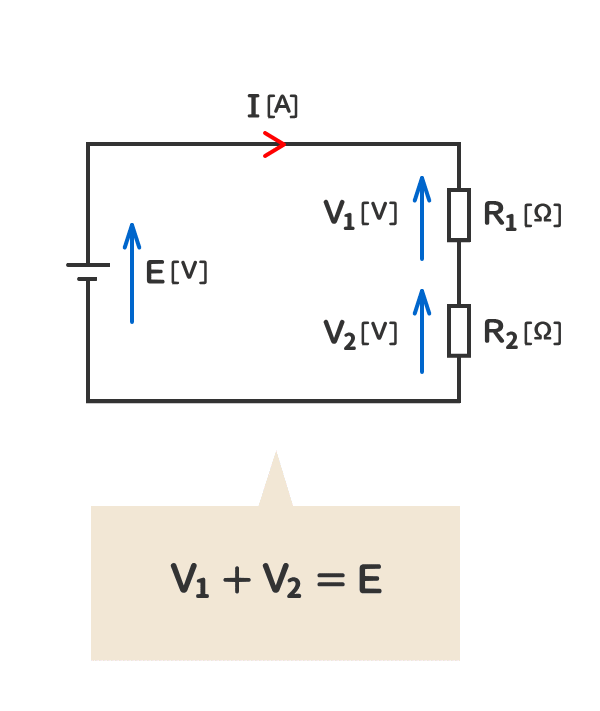
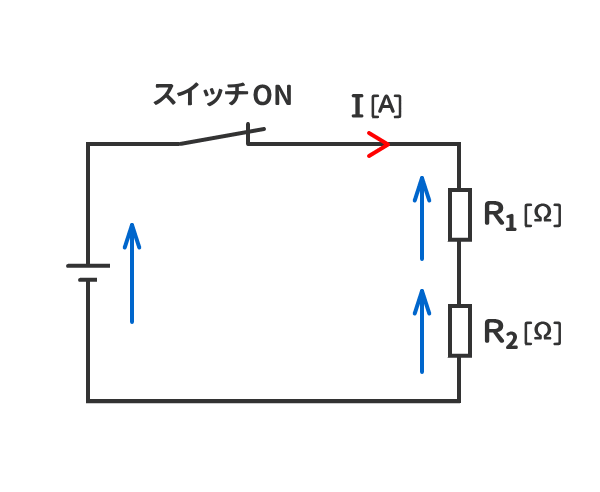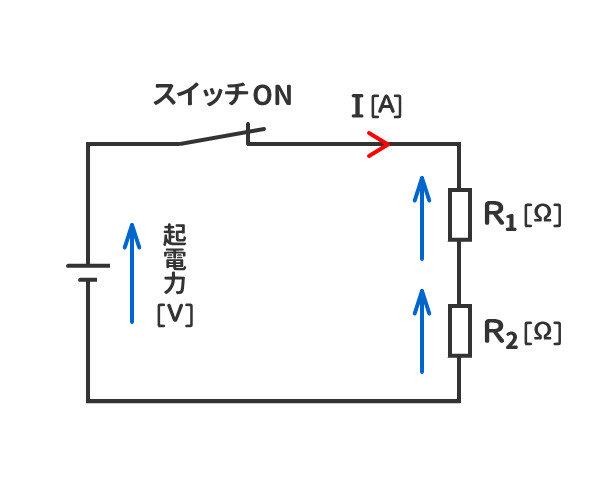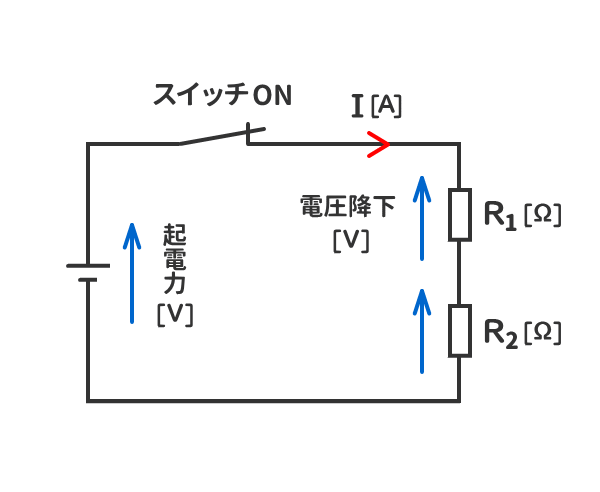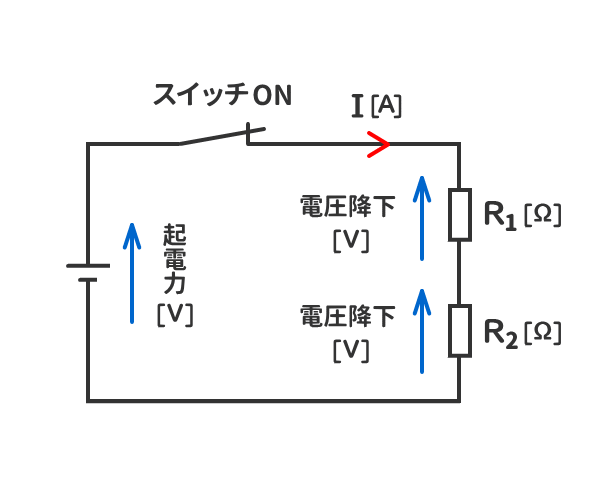
1. 抵抗が二つある場合のオームの法則
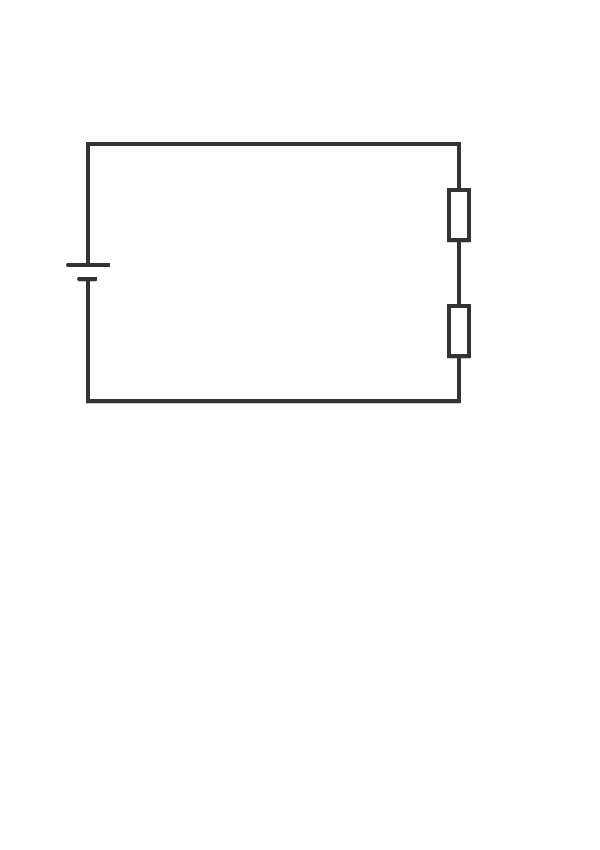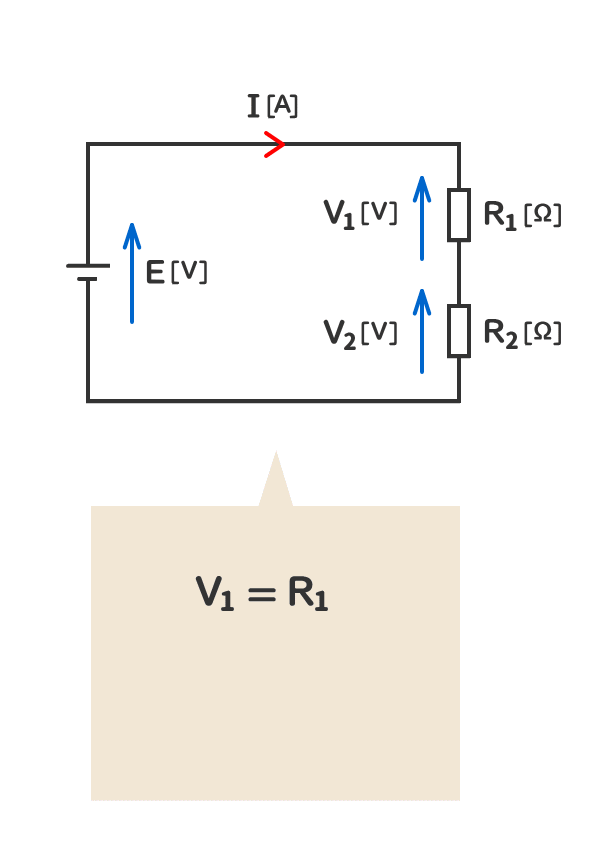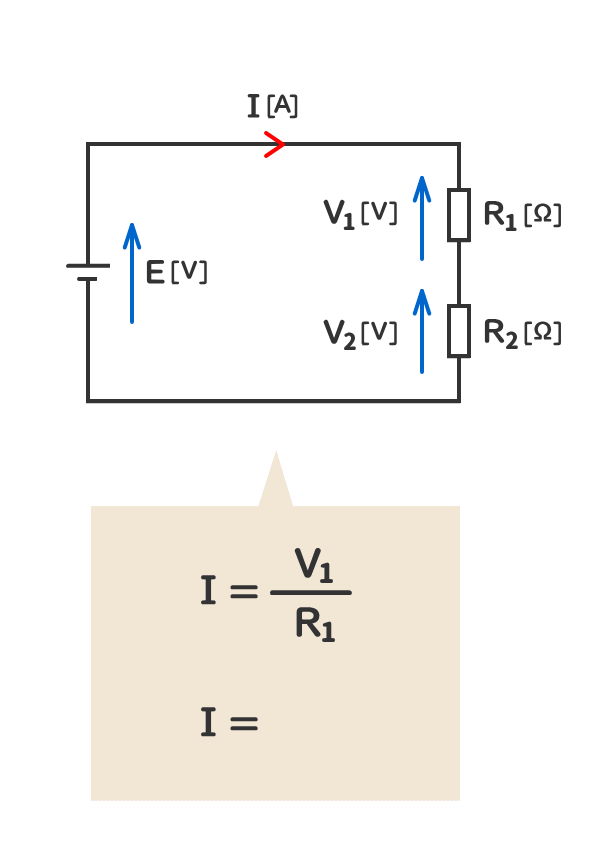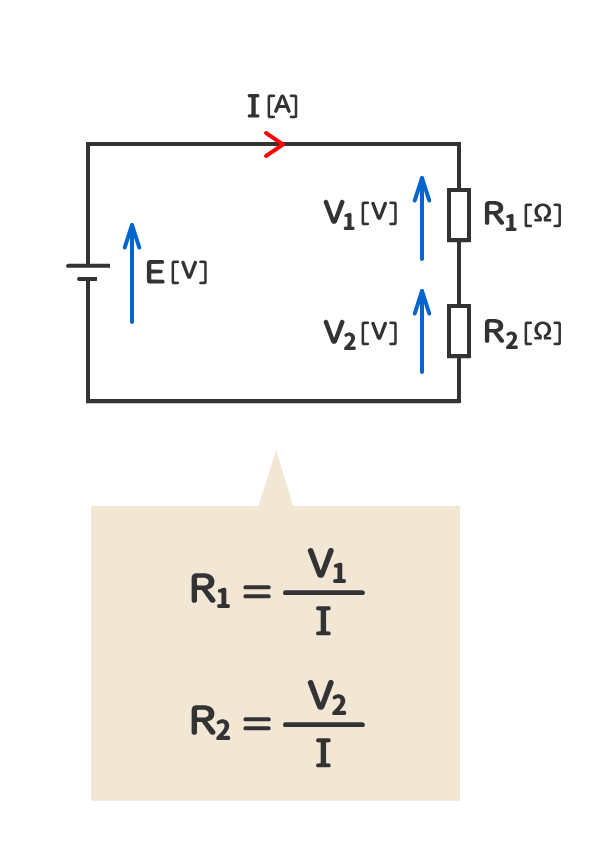
2. 当該の電気回路の抵抗の電圧の和は、電源の電圧と同じになる。
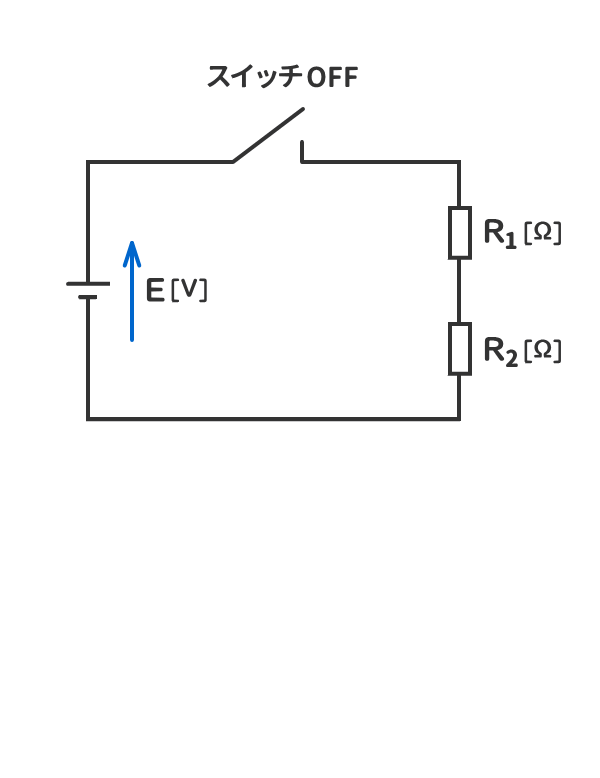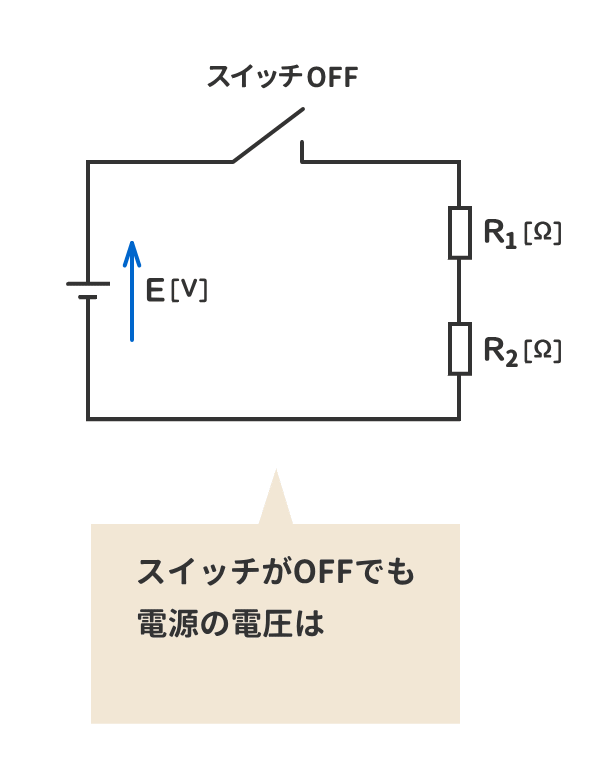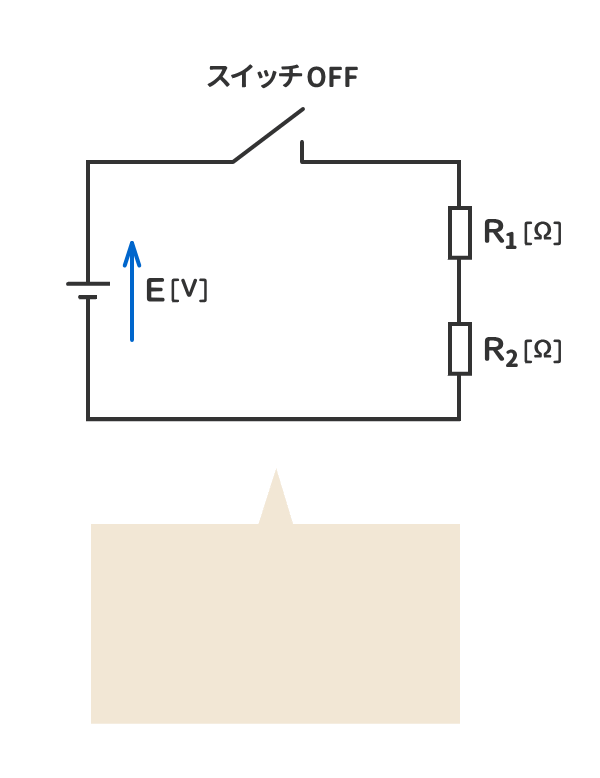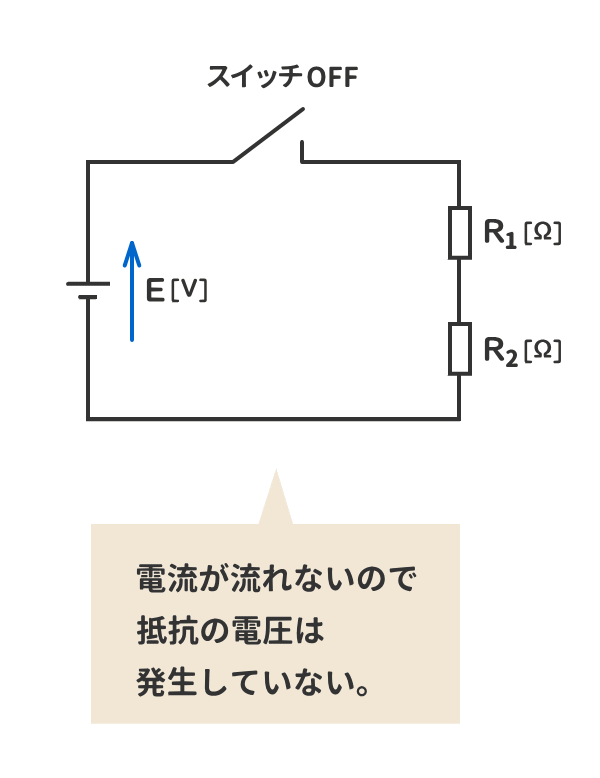
3. 電源の電圧はスイッチがOFFでも発生しているが、抵抗には電流が流れていないので、抵抗の電圧は発生しない。
4. 抵抗の電圧は、スイッチをONして抵抗に電流が流れることによって発生する。

5.電源の電圧と抵抗の電圧を区別するために、電源の電圧を「起電力」、抵抗の電圧を「電圧降下」と呼称することがある。
6.電流は、分流しても合流しても失われない。
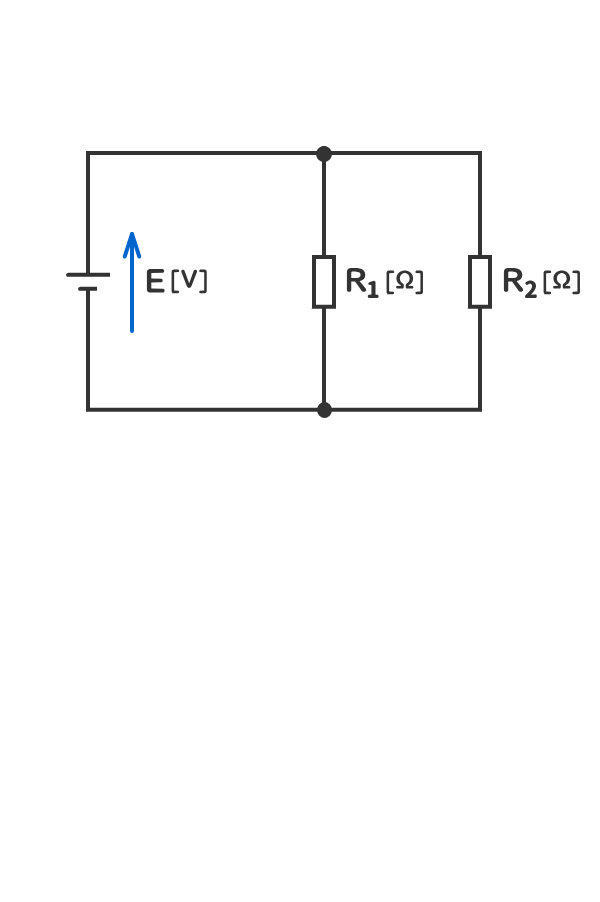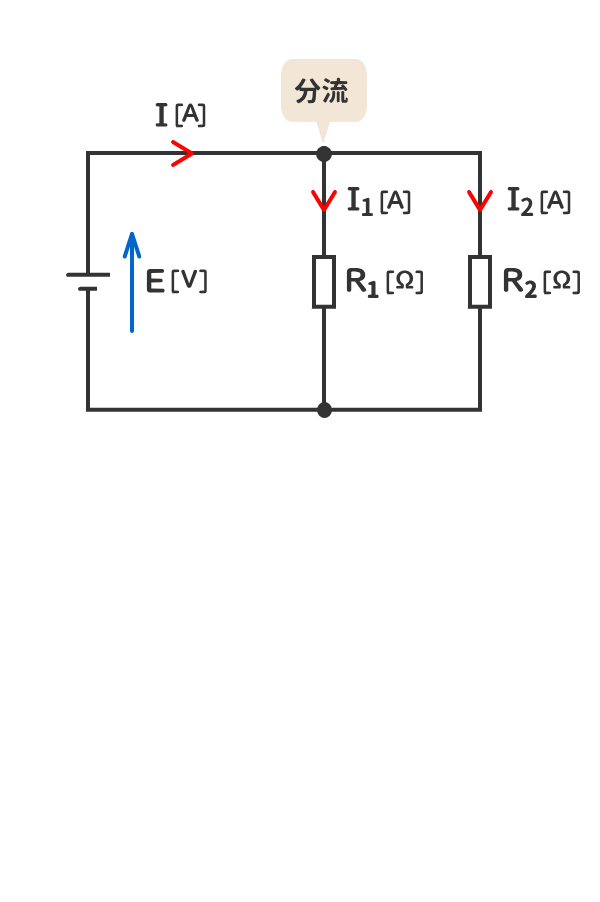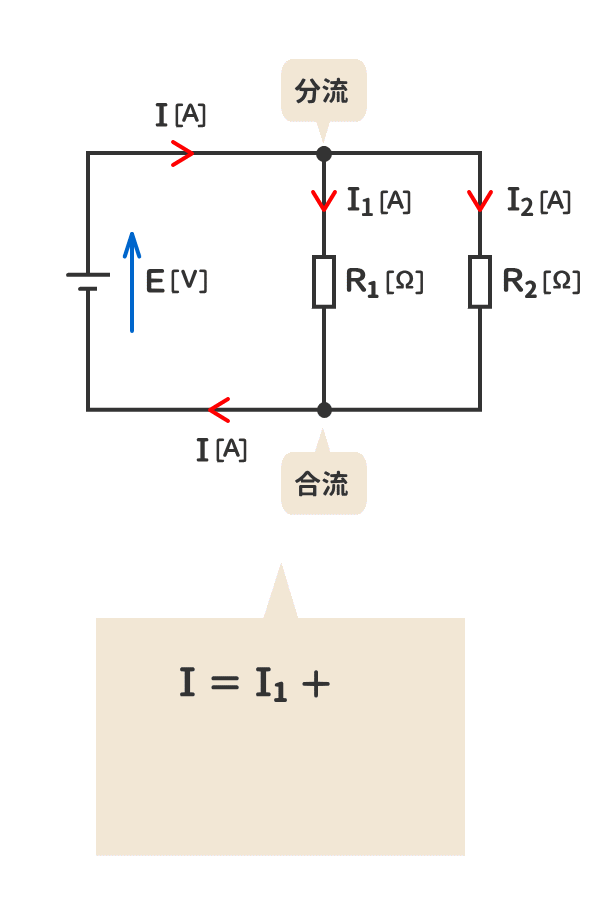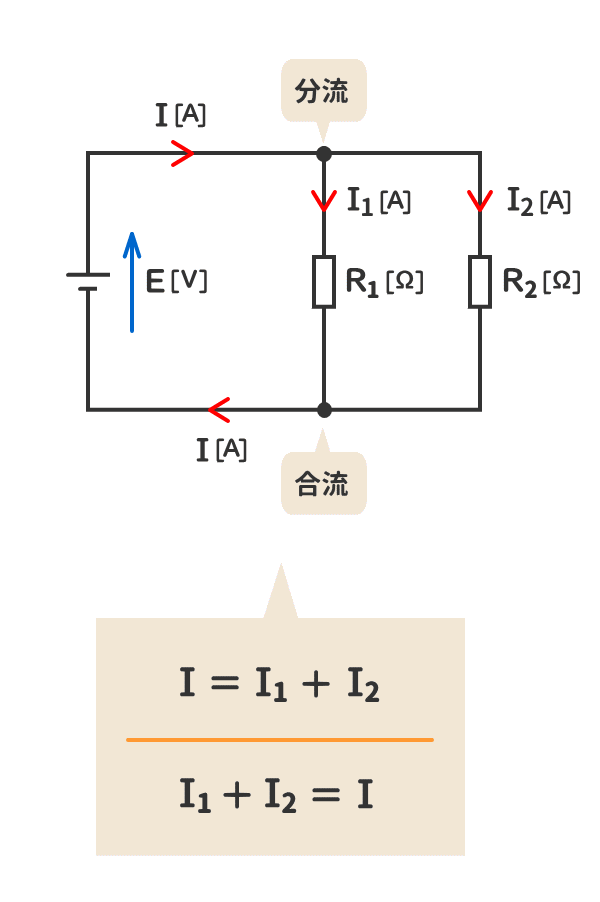
7.並列箇所に加わる電圧は同じである。
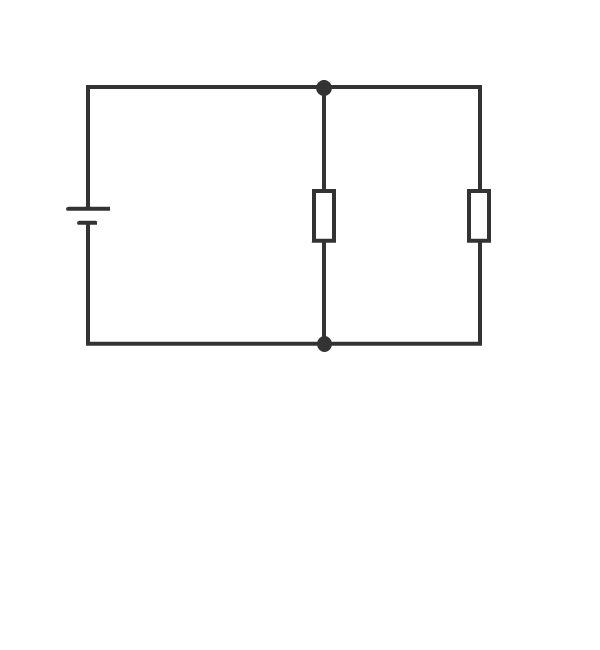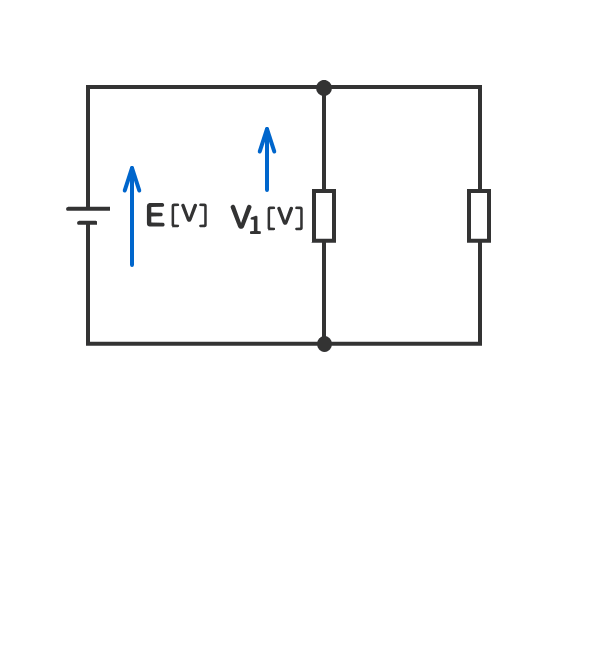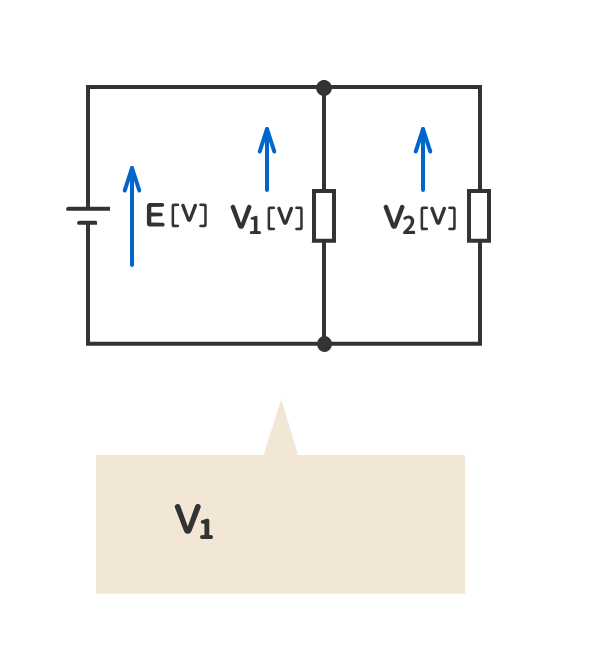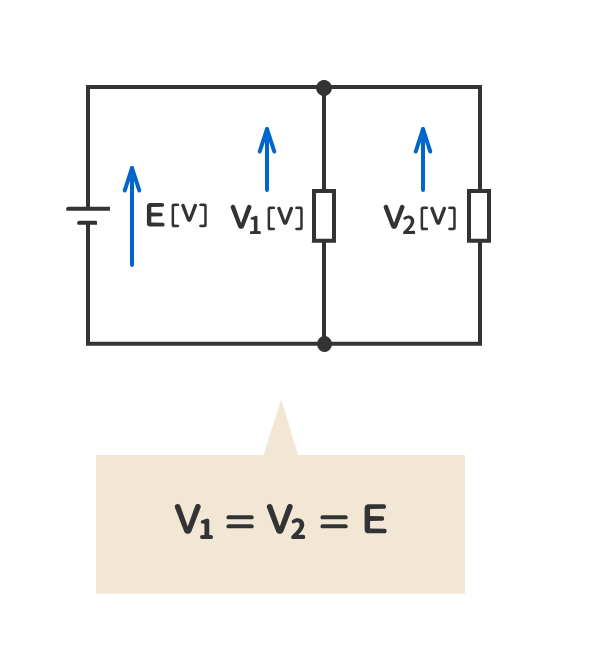
8.抵抗を直線上に接続することを「抵抗の直列接続」という。
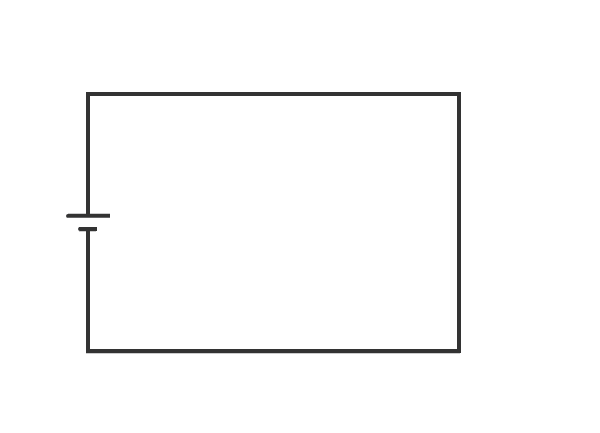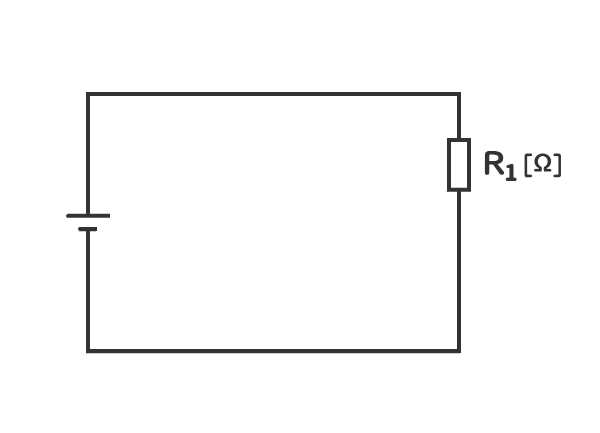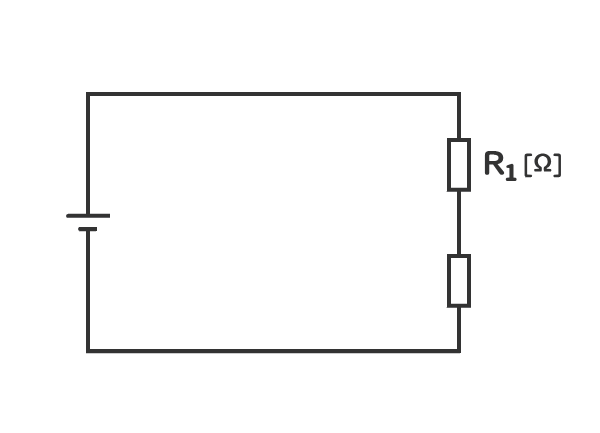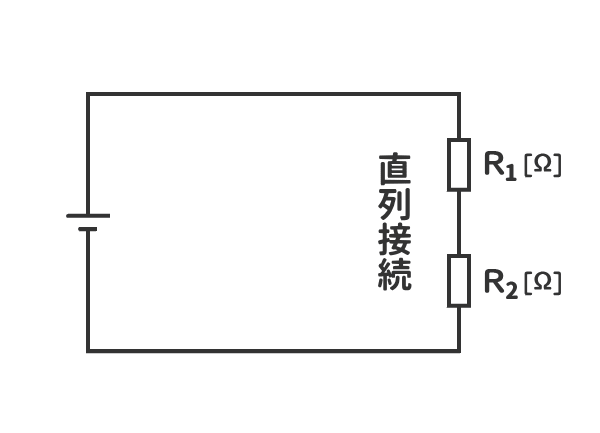
9.抵抗を並べて接続することを「抵抗の並列接続」という。

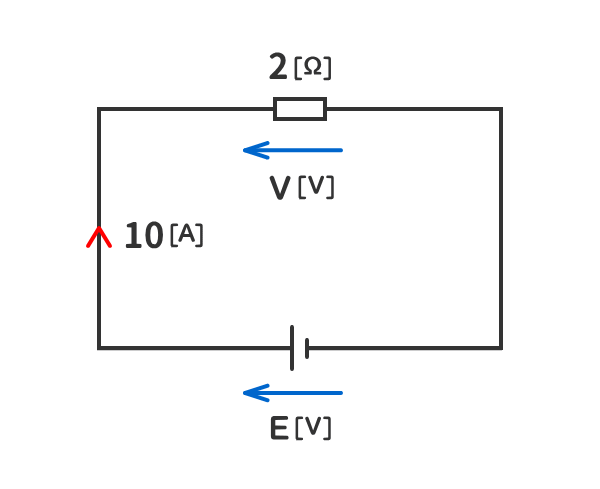
例題1
下図の回路の抵抗の電圧V[V]と電源電圧E[V]を求めよ。
解答を表示する

解答を非表示にする
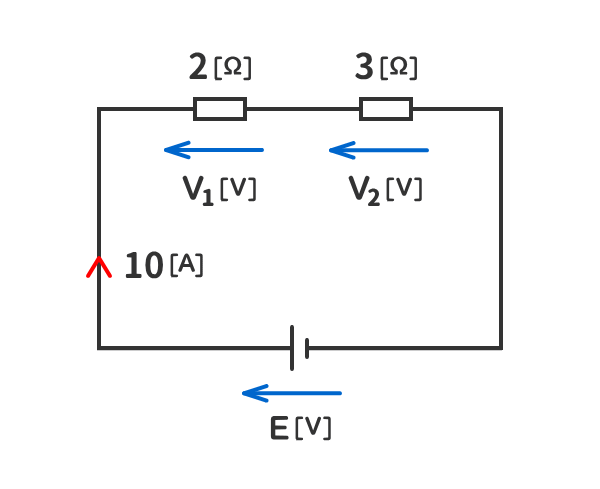
例題2
下図の回路の抵抗の電圧V1[V]とV2[V]および電源電圧E[V]を求めよ。
解答を表示する

解答を非表示にする
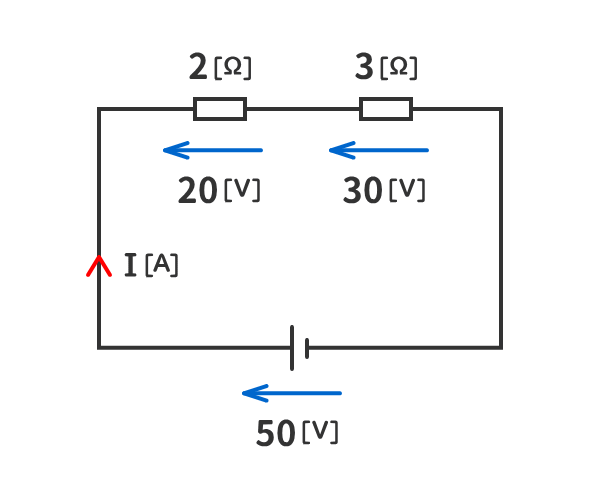
例題3
下図の回路に流れる電流I[A]を求めよ。
解答を表示する

解答を非表示にする
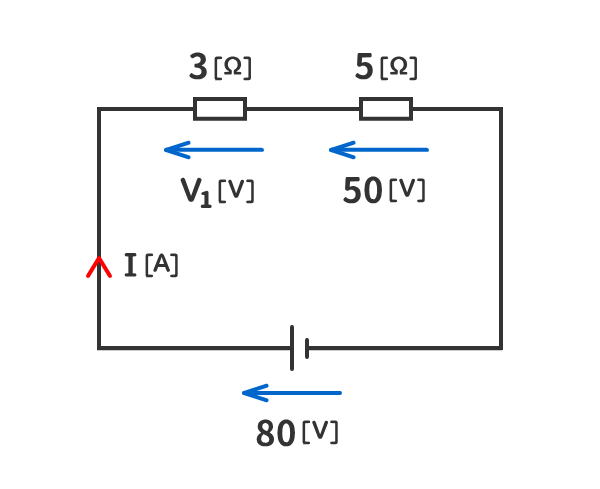
例題4
下図の回路の抵抗の電圧V1[V]を求めよ。
解答を表示する

解答を非表示にする
例題5
下図の回路の抵抗の電圧V1[V]とV2[V]および電源電圧E[V]を求めよ。
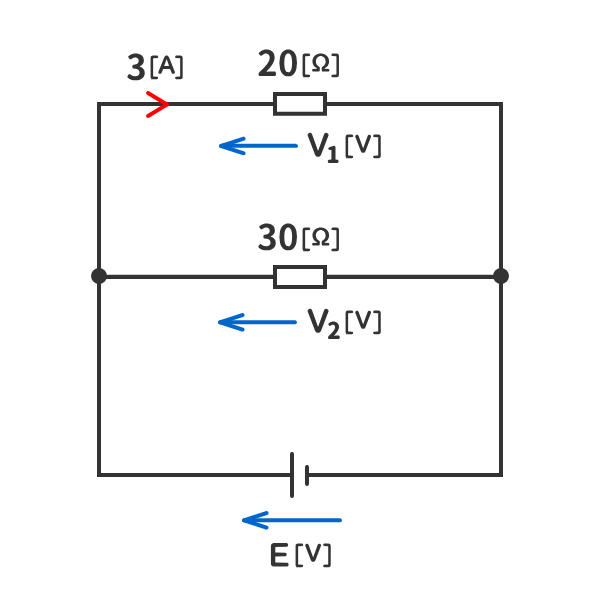
解答を表示する

解答を非表示にする
例題6
下図の回路の電流I1[A]とI2[A]とI[A]を求めよ。
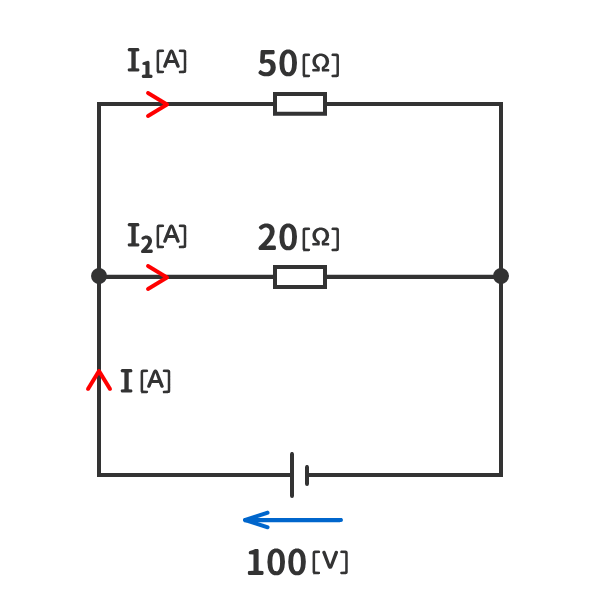
解答を表示する

解答を非表示にする
関連事項ピックアップ






