ミルマンの定理
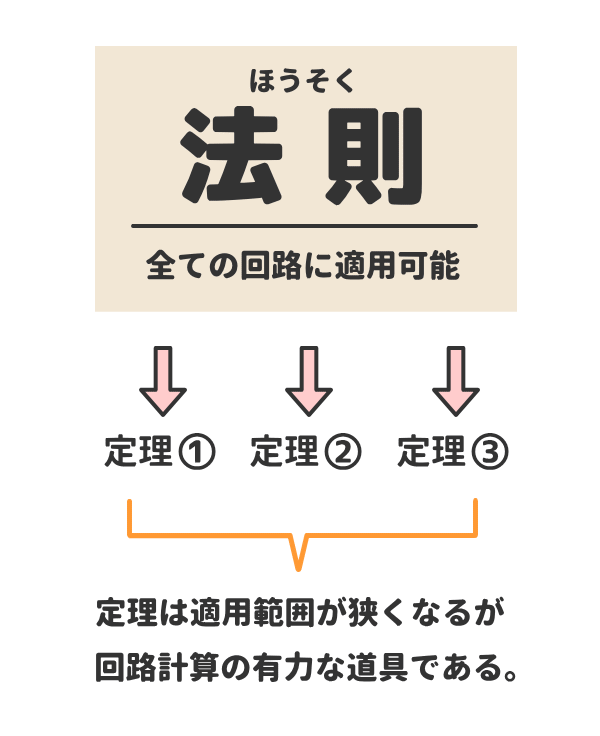
しかしながら、電気回路が複雑になるとこれらの法則を直接適用して計算するのが面倒になってくる。

そこで考えられたのが、法則から導かれた重要な結果を定理としてまとめておくことである。
これらの定理を電気回路に適切に適用することができれば、分圧式や分流式のように法則による計算過程を省略して知りたい結果を手早く得ることができるようになる。
ミルマンの定理は、電気主任技術技術者試験の有力な計算ツールのひとつになります。
目次
ミルマンの定理
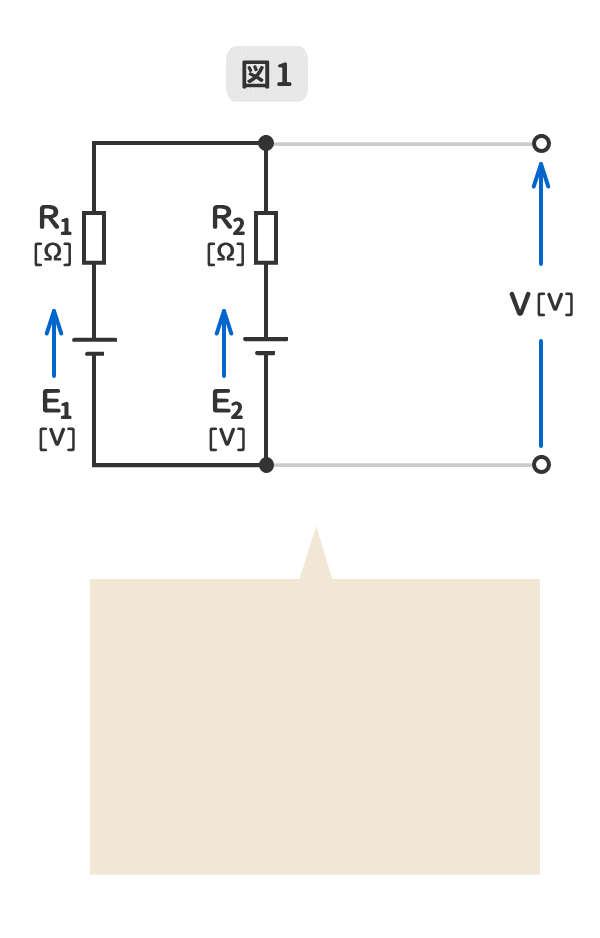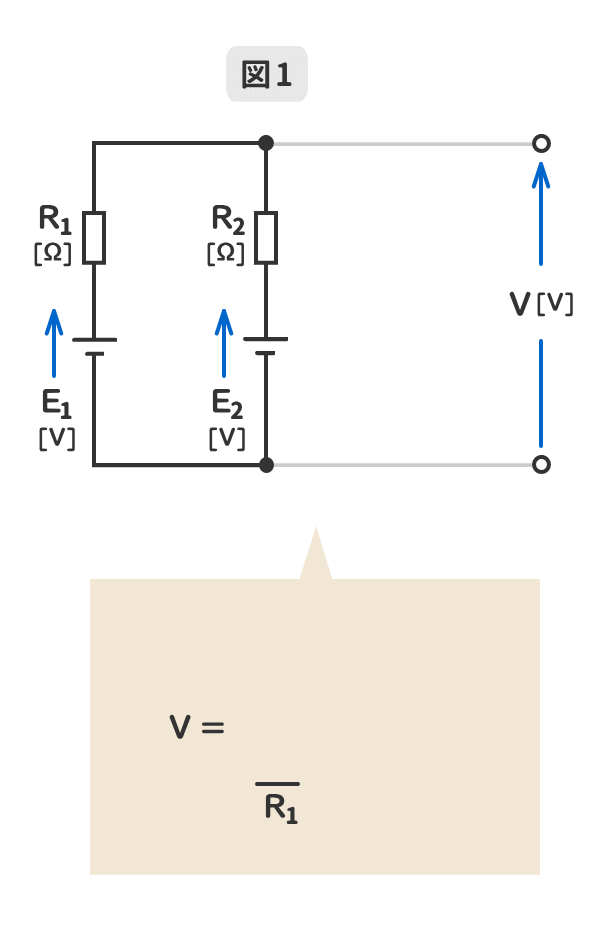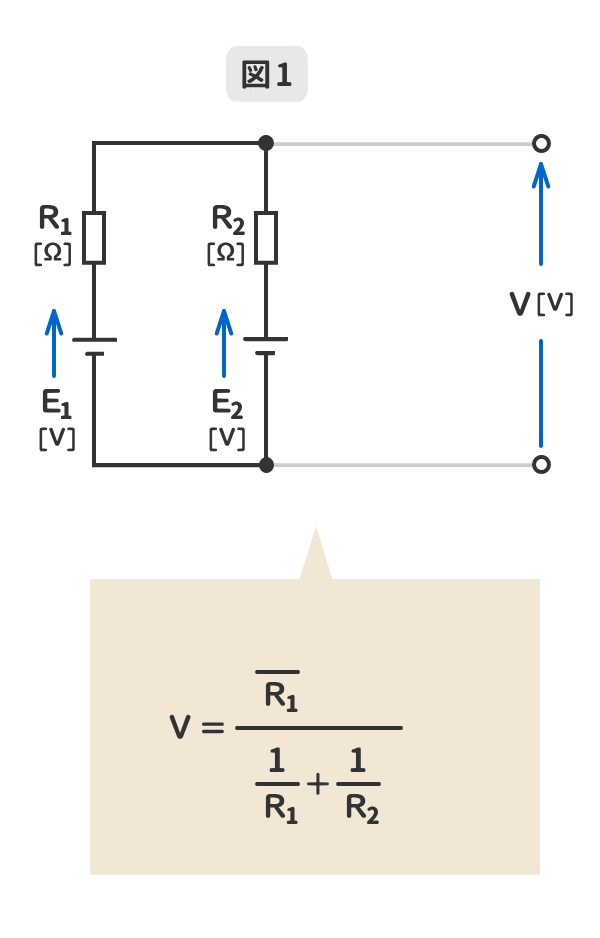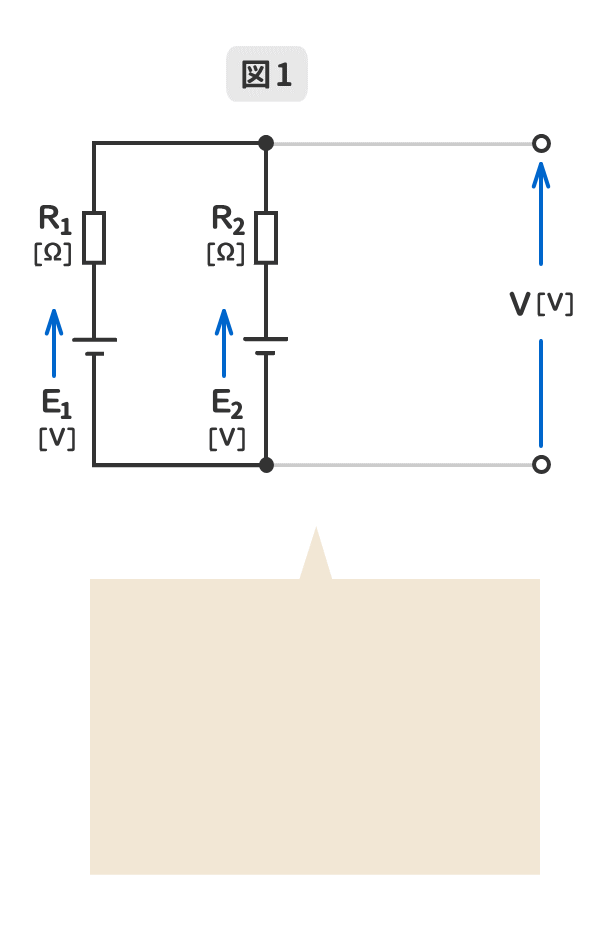
ミルマンの定理は、電源を並列に接続した回路の共通の端子電圧V[V]を簡単に求めるための定理である。
ここではミルマン定理の暗記と導出を行います。
ミルマンの定理の暗記はGIFアニメで何度も繰り返します。
1.電源の並列回路数が「2」のミルマンの定理を暗記しよう!
GIFアニメーションで動きます。
2.電源の並列回路数が「3」のミルマンの定理を暗記しよう!
GIFアニメーションで動きます。
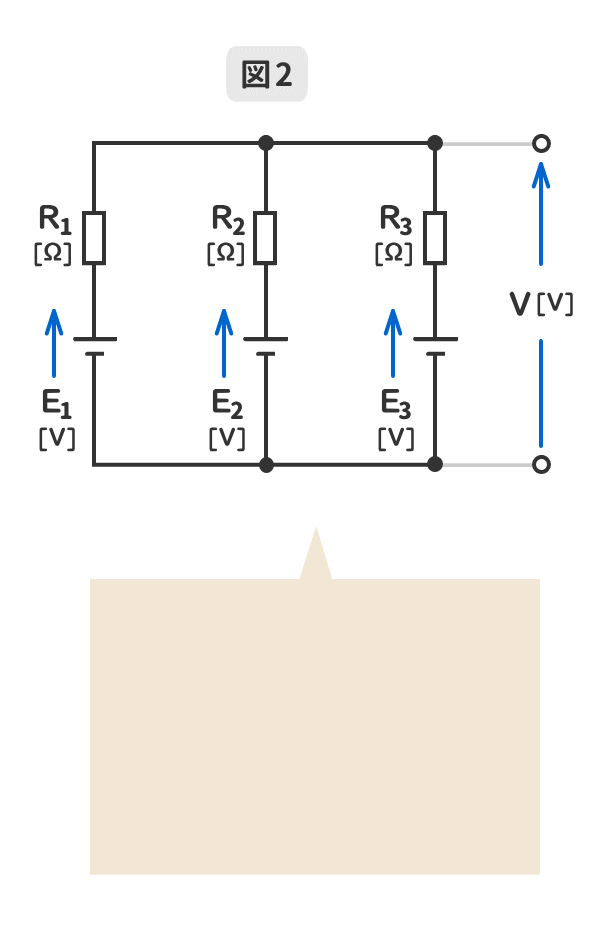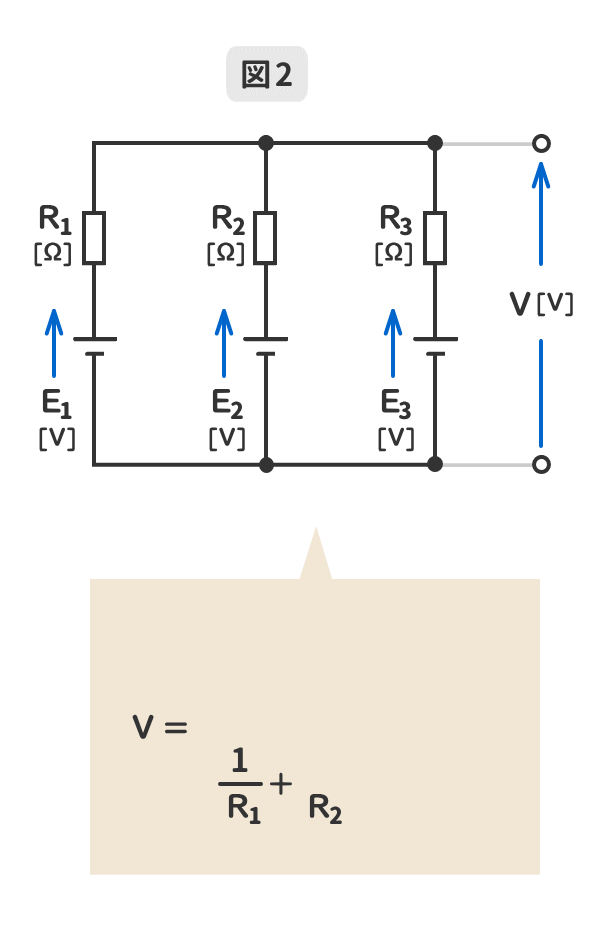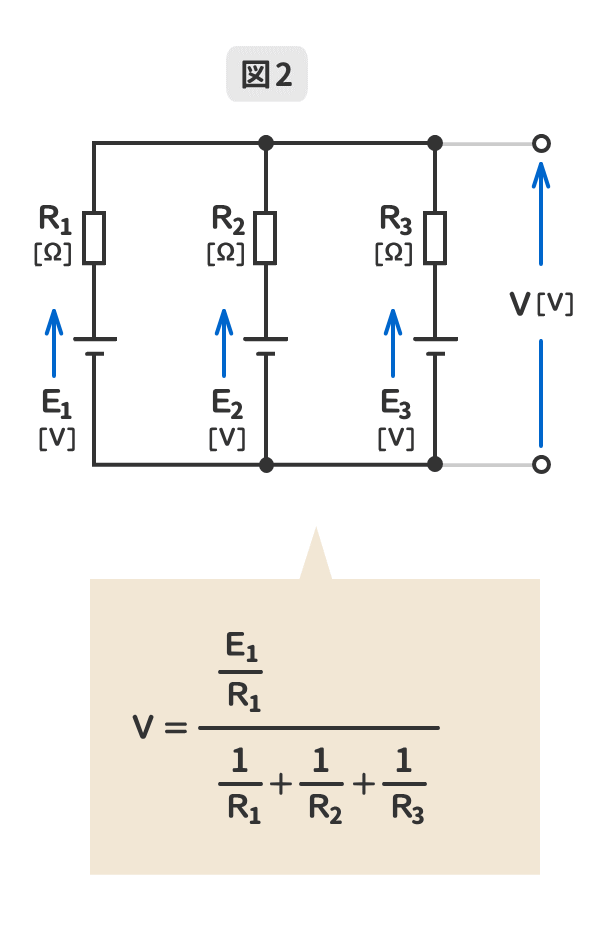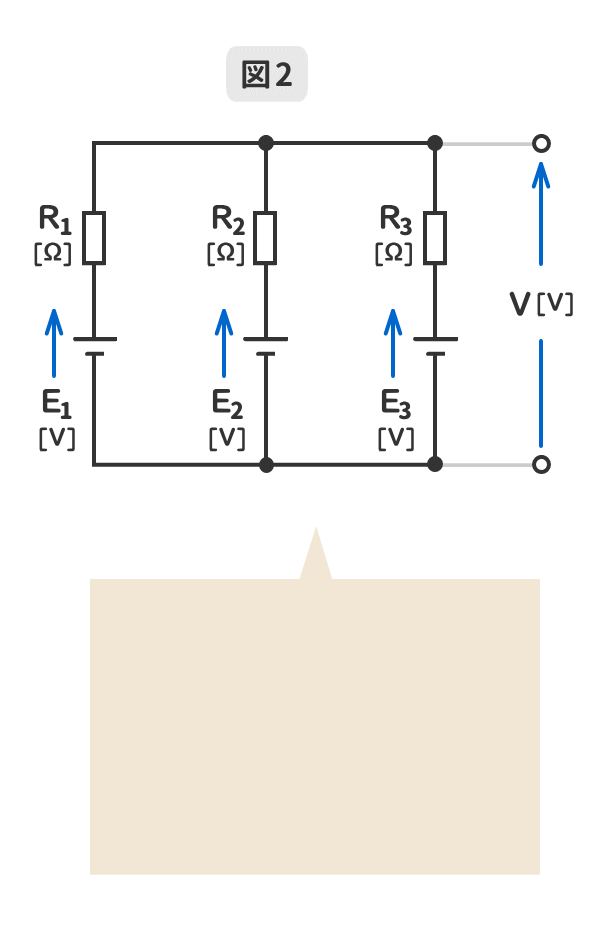
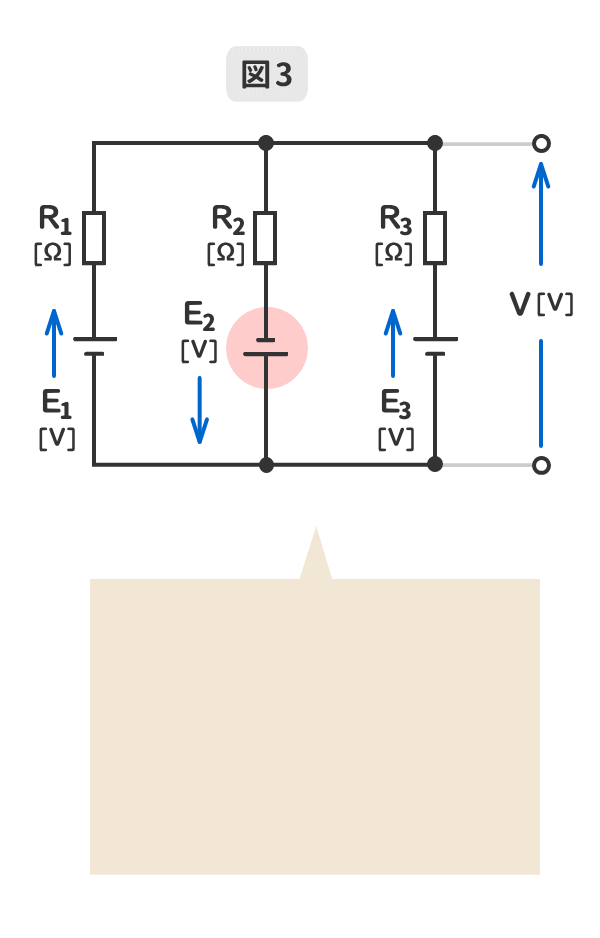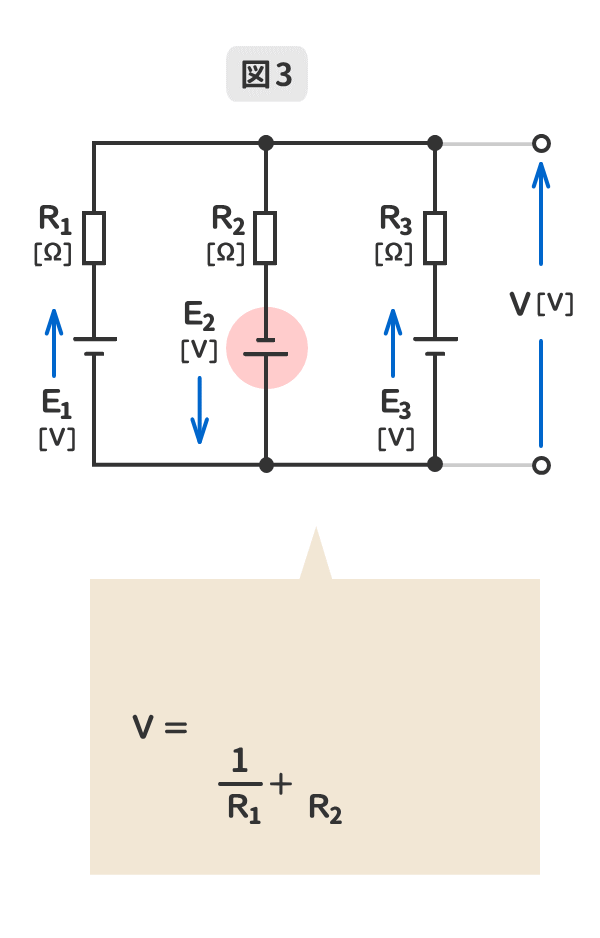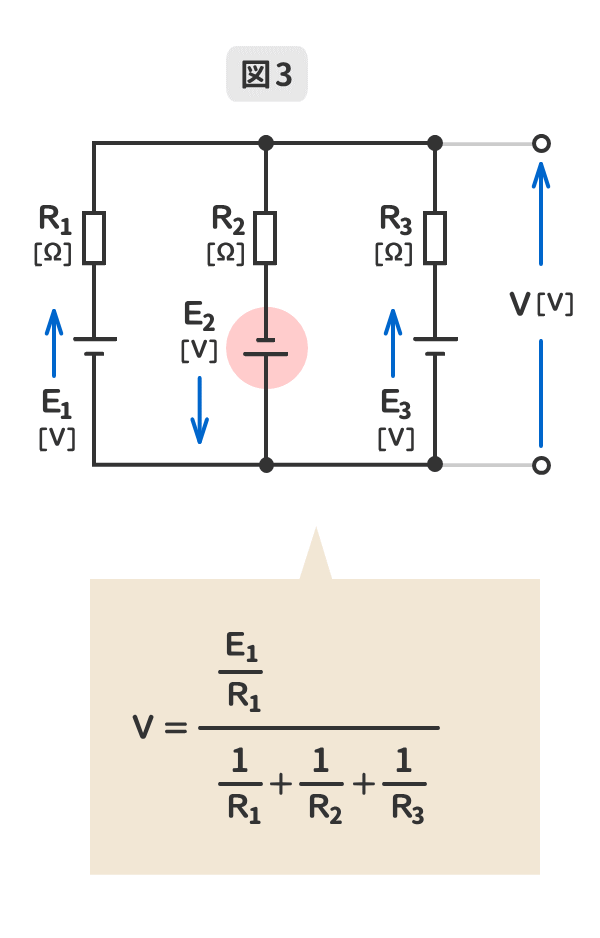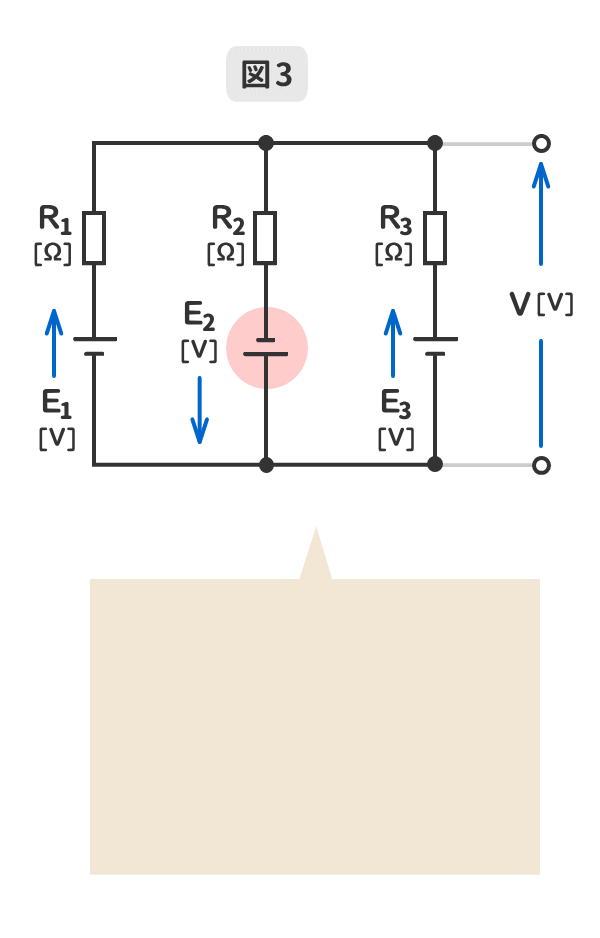
3.端子電圧と逆向きの電源が含まれている場合のミルマンの定理を暗記しよう!
GIFアニメーションで動きます。
4.電源の並列回路数が「2」のミルマンの定理の導出
キルヒホッフの第2法則を適用します。

5.電源の並列回路数が「3」のミルマンの定理の導出
キルヒホッフの第1法則と第2法則を適用します。
基本的には前項と同等の手順で確認します。
確認が面倒な方は前項の「2」でミルマンの定理を認めて下さい。

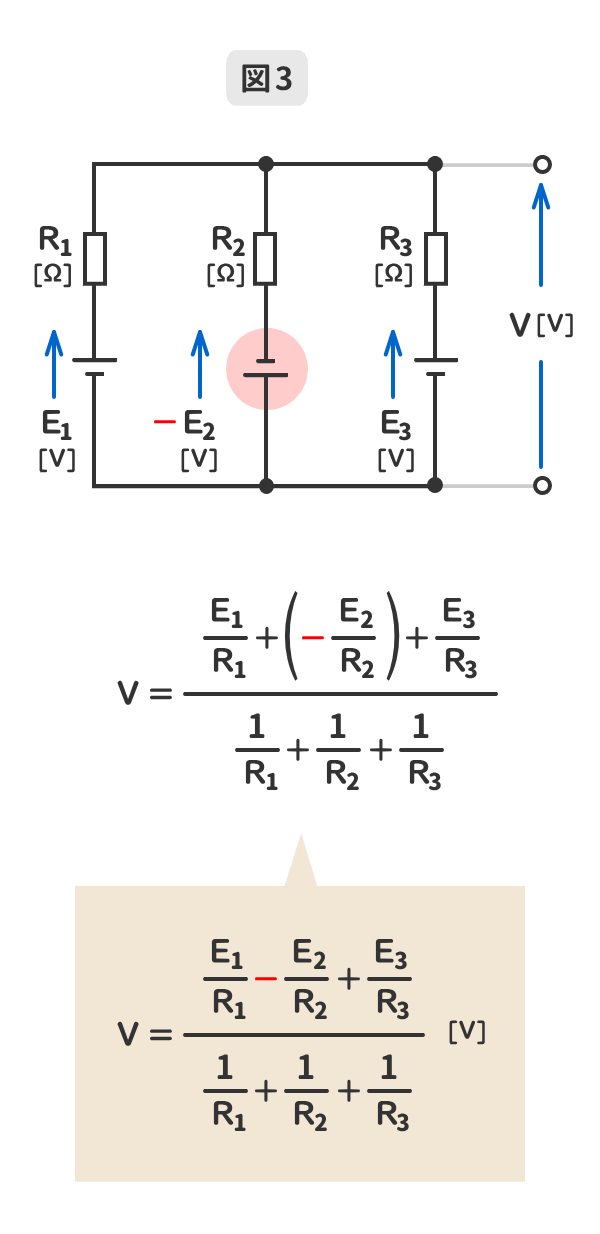
6.逆向きの電源が含まれる場合のミルマンの定理の導出
逆向きの電源の電圧の向きを「端子電圧の向きに合わせる」と電圧の符号が反転する。
その状態でミルマンの定理を適用すればよい。
例題1
下図の回路の端子電圧V[V]を求めよ。

解答を表示する
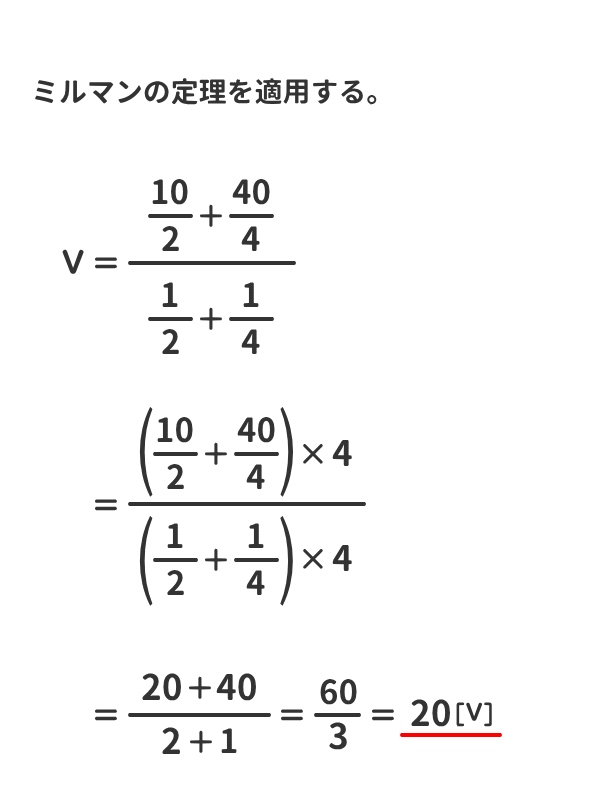
解答を非表示にする
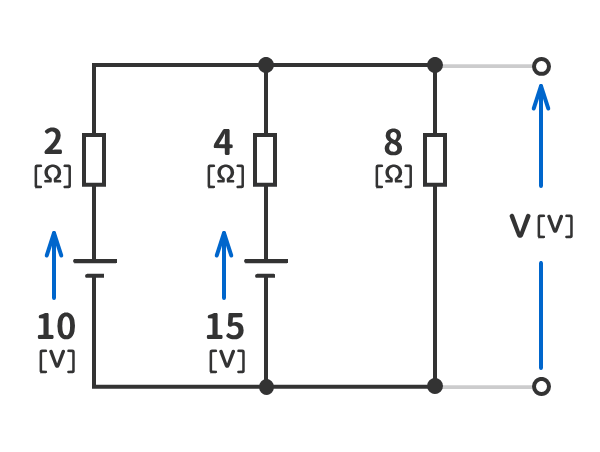
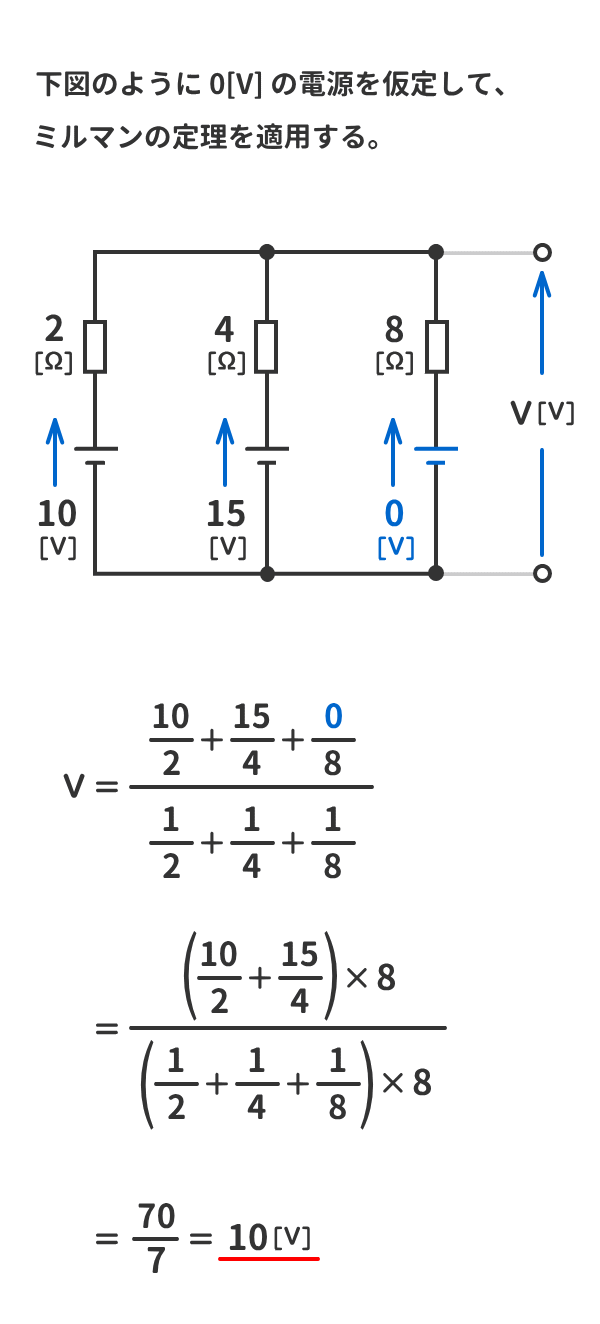
例題2
下図の回路の端子電圧V[V]を求めよ。
解答を表示する
解答を非表示にする
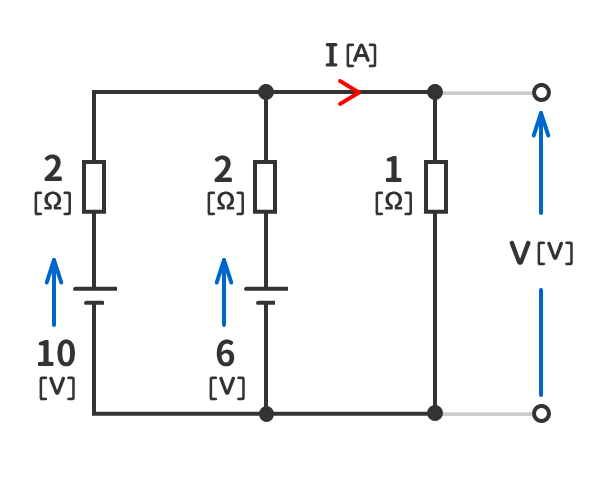
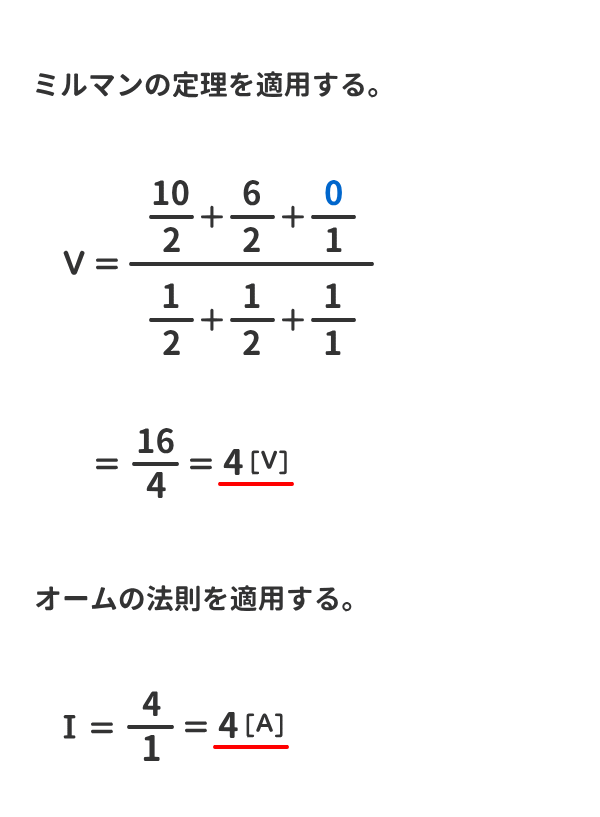
例題3
下図の回路の端子電圧V[V]と電流I[A]を求めよ。
解答を表示する
解答を非表示にする
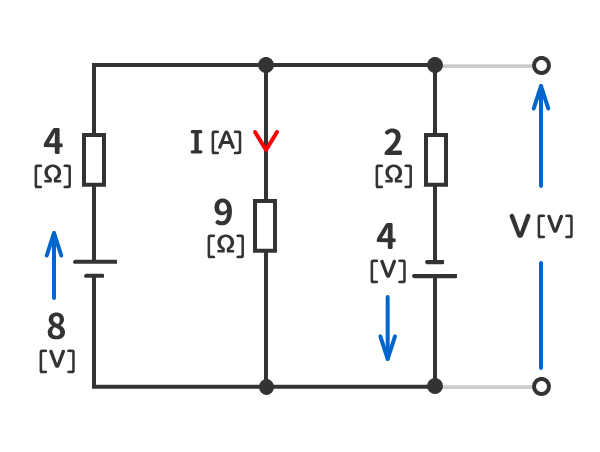
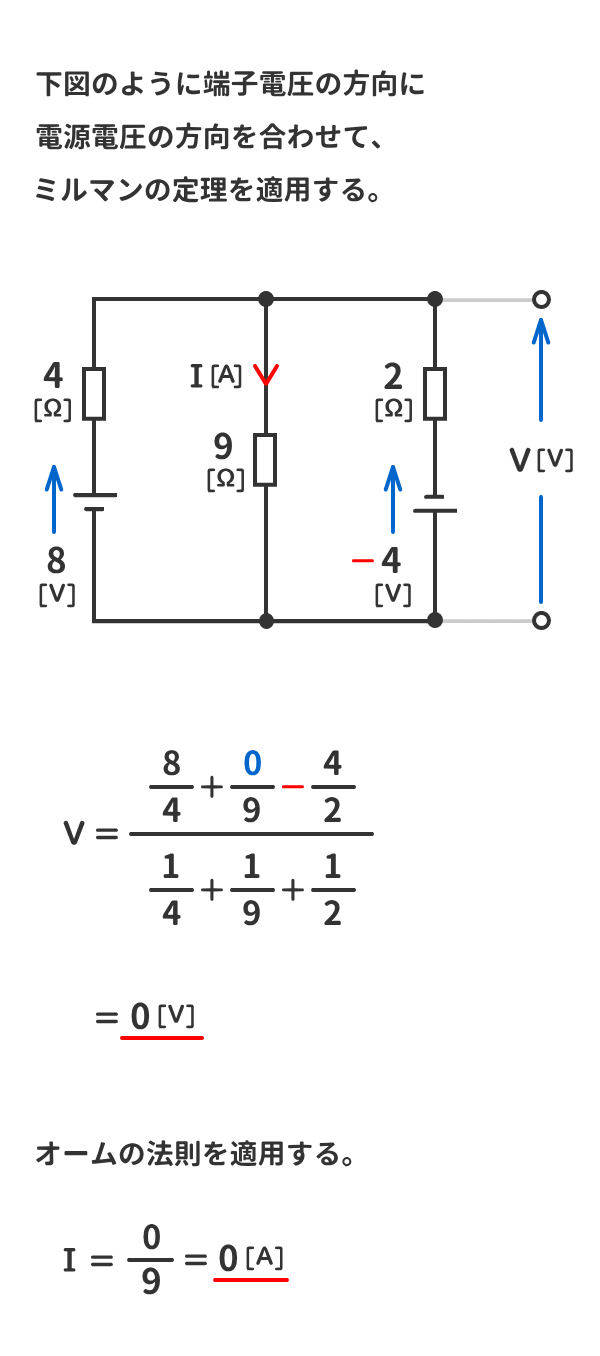
例題4
下図の回路の端子電圧V[V]と電流I[A]を求めよ。
解答を表示する
解答を非表示にする
関連事項ピックアップ






