電験2種に必要な微分積分学の概要
電験2種の学習内容を理解するためには、微分積分学の知識が必須となります。
ただし、微分と積分の公式を単に暗記するだけでは不十分です。
それらの公式がどのような考え方で導かれたのかを理解した上で暗記しなければなりません。

ここでは私が電験2種を受験したときの電気数学ノートを元に、微分積分学の学習の勘所(ポイント)をまとめました。
また公式の羅列だけではなく練習問題もあるので、知識の定着に役立つことでしょう。
これらの内容は、電験2種の学習を飛躍的に進めるためキッカケになるものであると確信しています。
目次
1.微分の定義
微分法とは、関数y=f(x)の曲線の傾きについての計算に関するもので、導かれる結果は導関数(どうかんすう)と呼ばれているものである。
関数y=f(x)とは、二つの変数xとyがあるとき、xの値に対してyの値が一つに定められる関係にあるものをいう。
このとき、変数yはxの値に従属しているので従属変数といい、xは独立しているので独立変数と呼ばれている。
もし、yが時間tについての関数であれば、y=f(t)と表記すればよい。
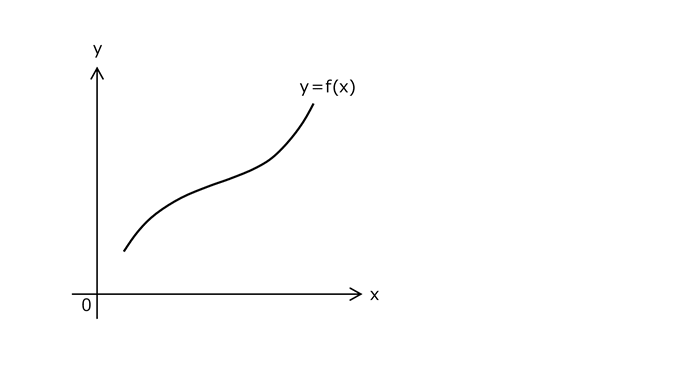
1.1 関数y=f(x)
下記の関数の曲線は、一般的な関数を示すために書いた曲線であり、代表的な関数の曲線に限定されないことを示したものです。
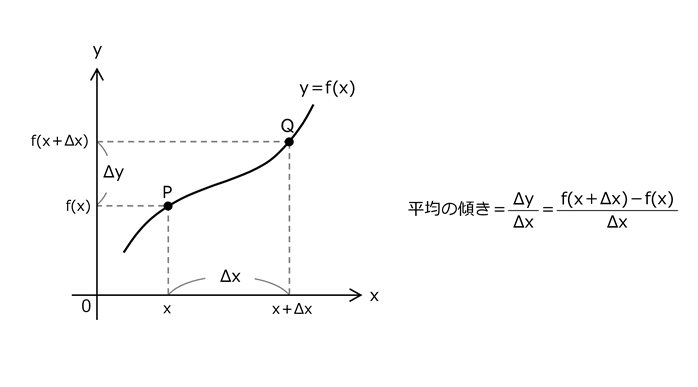
1.2 点Pと点Qの平均の傾き
平均の傾き(平均変化率)とは、y軸方向の増分Δyをx軸方向の増分Δxで割ったものである。
Δは微小を意味しているが、図では見やすくするために微小な増分とはなっていません。
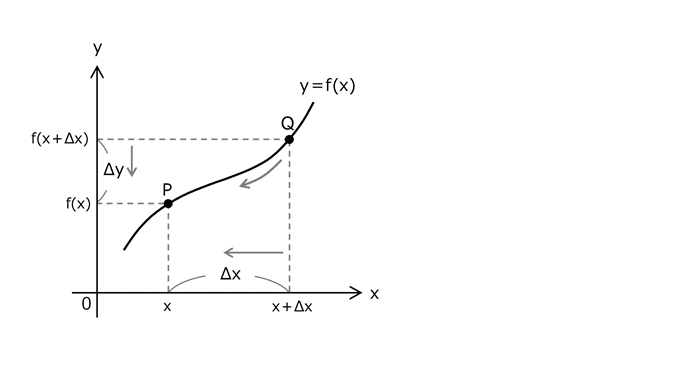
1.3 点Pの正確な傾きの反映
平均の傾きを、点Pの傾きとして正確に反映させる操作は、点Qを点Pに限りなく近づけることによって行われる。
数学的には、限りなく近づける操作を極限(きょくげん)といい、lim(リミット)という記号を用いて表す。
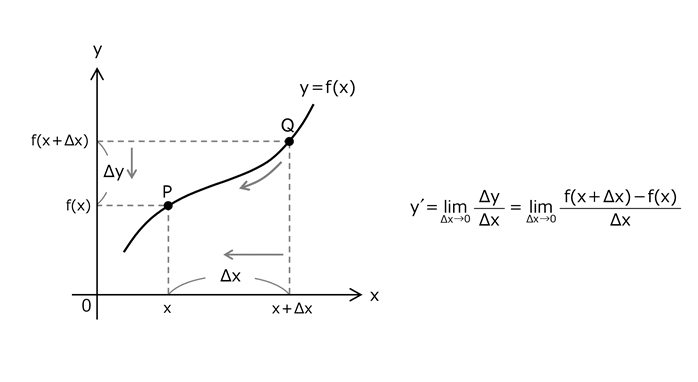
1.4 点Pの導関数の定義
1.3の操作の結果で導かれた正確な傾きの関数を導関数といい、y’やdy/dxの記号で表記する。
また、関数y=f(x)の導関数を求めることを微分(びぶん)と呼んでいる。
2.微分の公式の意味と価値
関数y=f(x)の導関数は式(1)で定義されるので、対象の関数を式(1)に適用すれば導関数を求めることができる。
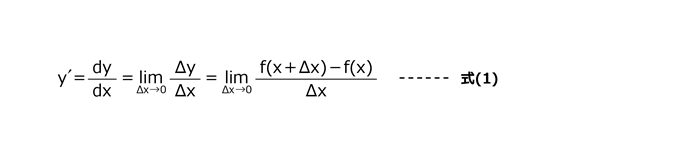
しかしながら、全ての関数に対して式(1)を適用していたのでは、計算に時間がかかってしまう。
そこで、電気工学で頻繁に使う代表的な関数については、式(1)の過程を省略するための公式化を行わなければならない。
この公式化を行ったものが微分公式であり、電験2種の学習を理解するために必要不可欠なものとなるわけです。
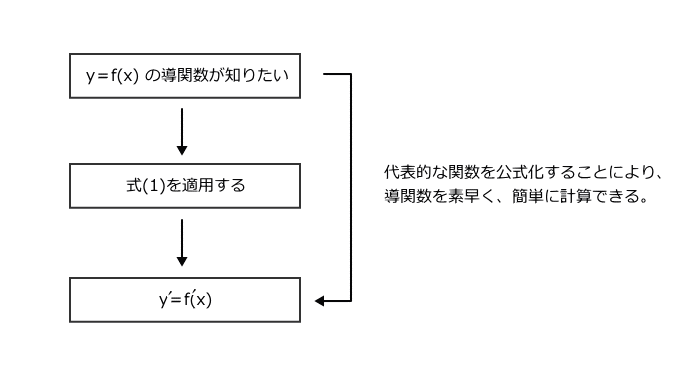
2.1 電気工学で頻繁に使う代表的な関数

3.微分公式の一覧と導出
ここでは、微分公式の一覧と微分公式の導出を示しておきます。
電験2種では、これ以外の微分公式が必要になる場合がありますが、学習の初期段階においては十分です。
もし、お手持ちの数学書または電験2種用の数学書に微分公式の導出の過程が載っていないならば、ハッキリいって役にたちませんので、買い直すことをお勧めします。
また、単に微分公式を暗記することは絶対にダメです。何故なら、微分公式の導出を理解するということは積分の理解に直結するからです。
暗記に暗記を重ねると袋小路に迷い込むので、このことは忘れないようにして下さい。
3.1 微分公式の一覧

初めての方は、微分公式の導出は、サラッと読み進めて下さい。
微分法の一般規則の知識が必要になります。
3.2 対数関数の微分公式の導出例

3.3 累乗関数の微分公式の導出例

3.4 指数関数の微分公式の導出例

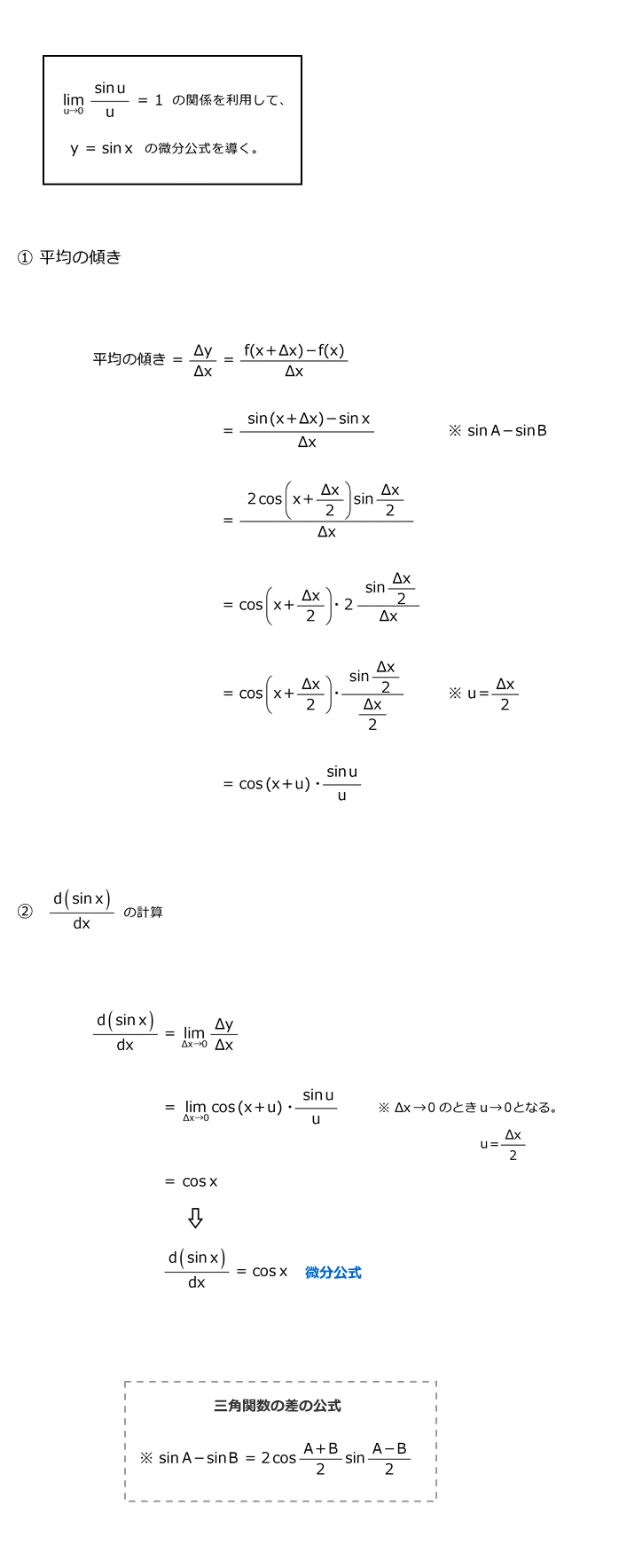
3.5 三角関数y=sinxの微分公式の導出例
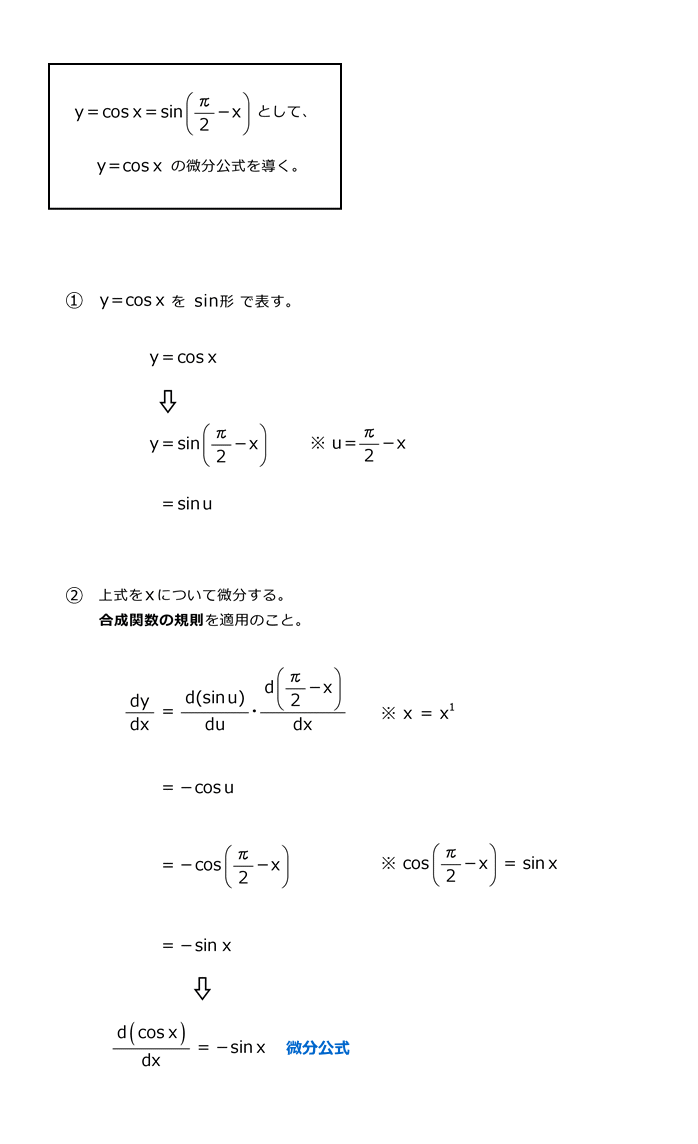
3.6 三角関数y=cosxの微分公式の導出例
3.7 三角関数y=tanxの微分公式の導出例

4.微分法の一般規則と導出
微分公式と同様に、式(1)の導関数の定義式から、下記の一般規則を導くことができます。
どれも重要な規則なので、必ず確認しておいて下さい。
軽視しがちな定数の規則は、積分で重要な意味を持ちます。
合成関数の規則は、非常に重要なので活用例とイメージを示しておきました。
4.1 定数の規則

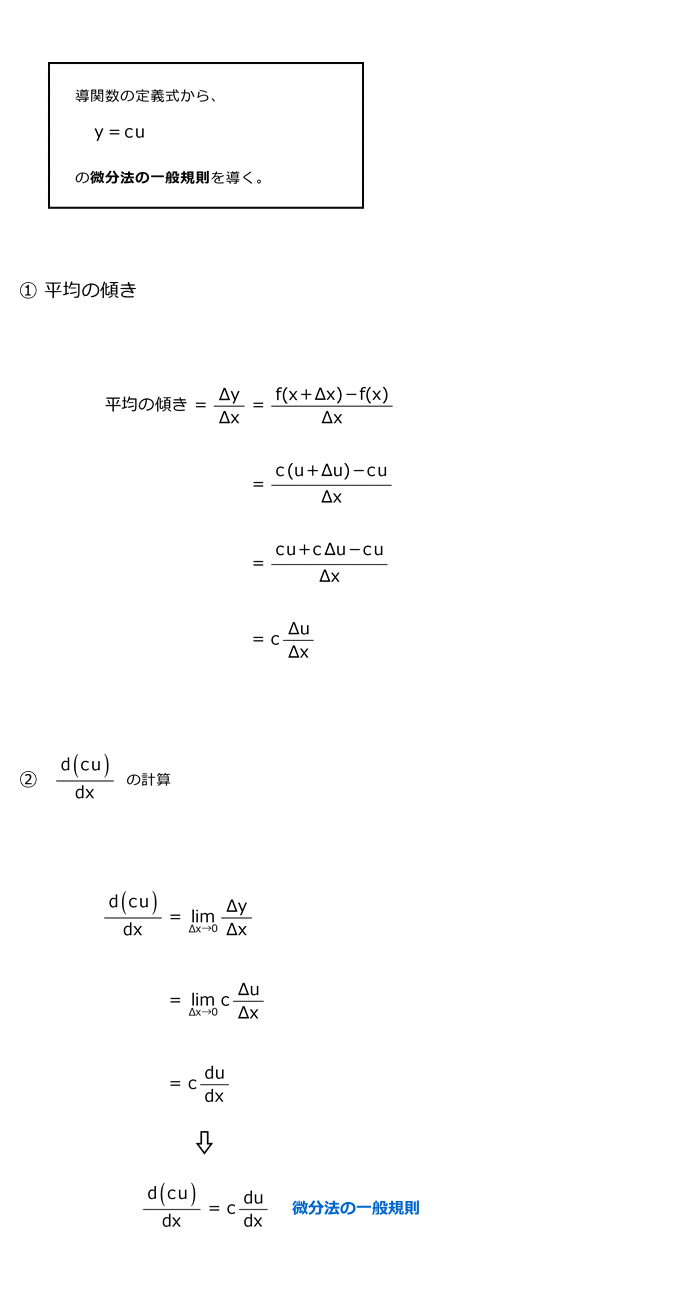
4.2 定数と関数の積の規則
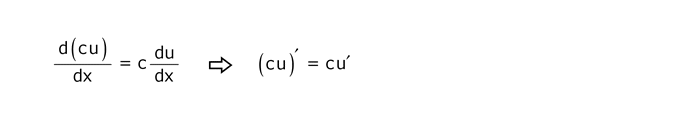
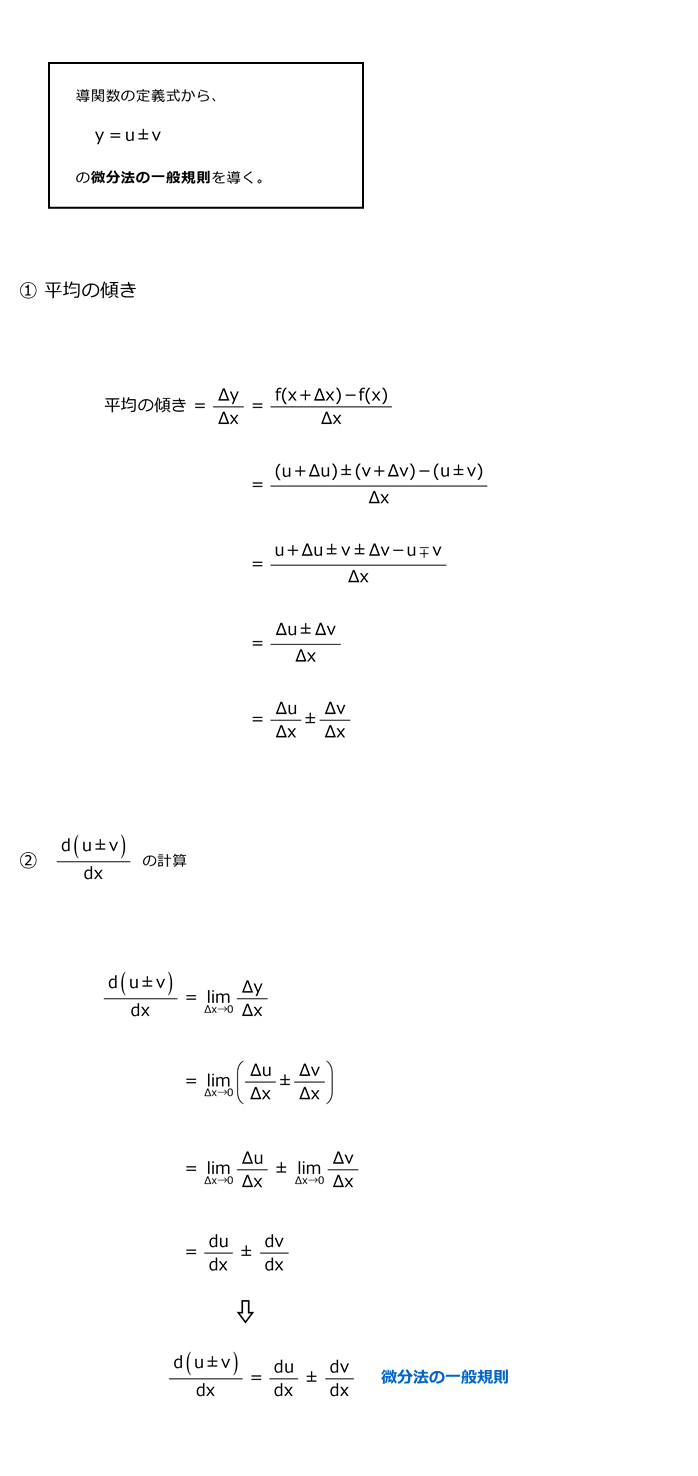
4.3 二つの関数の和あるいは差の規則
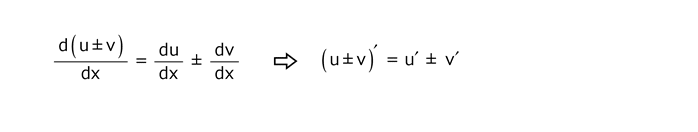
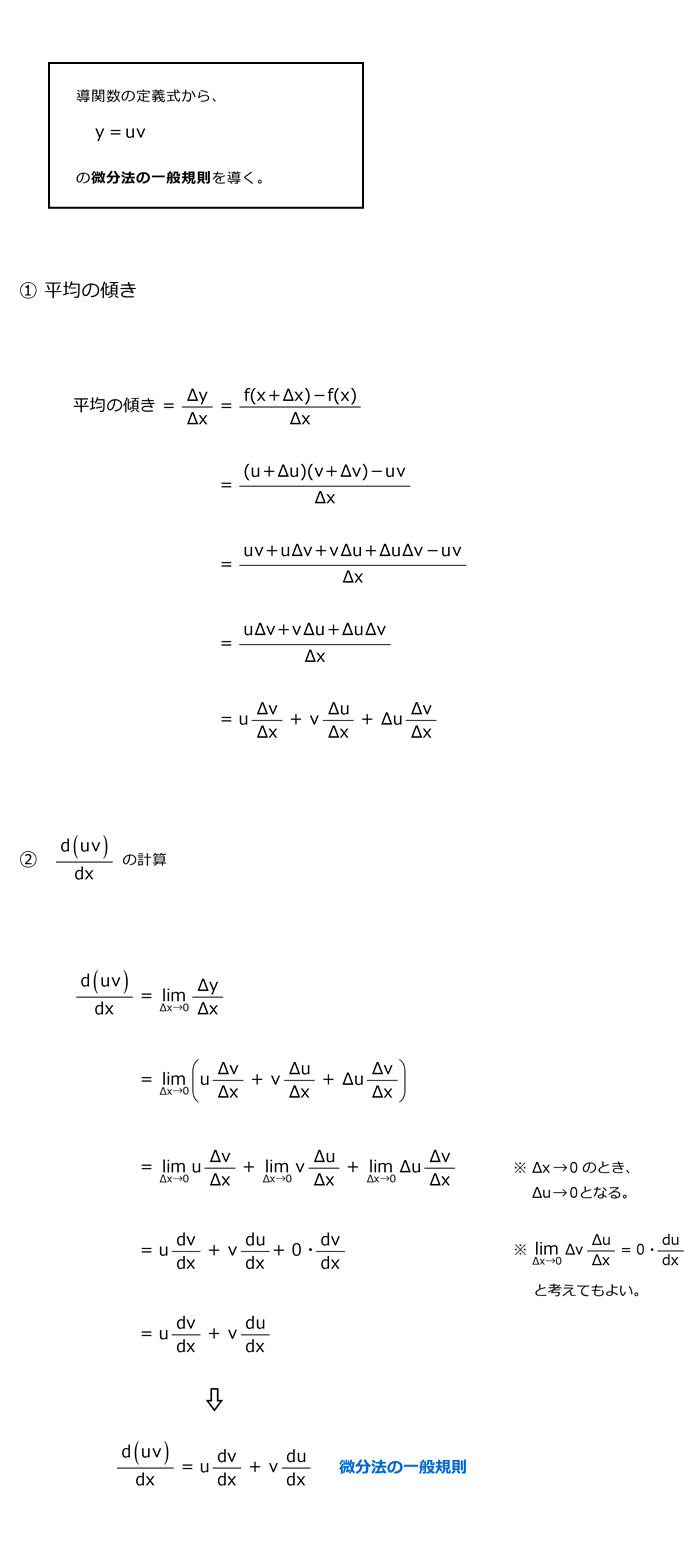
4.4 二つの関数の積の規則
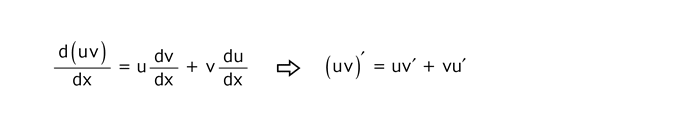
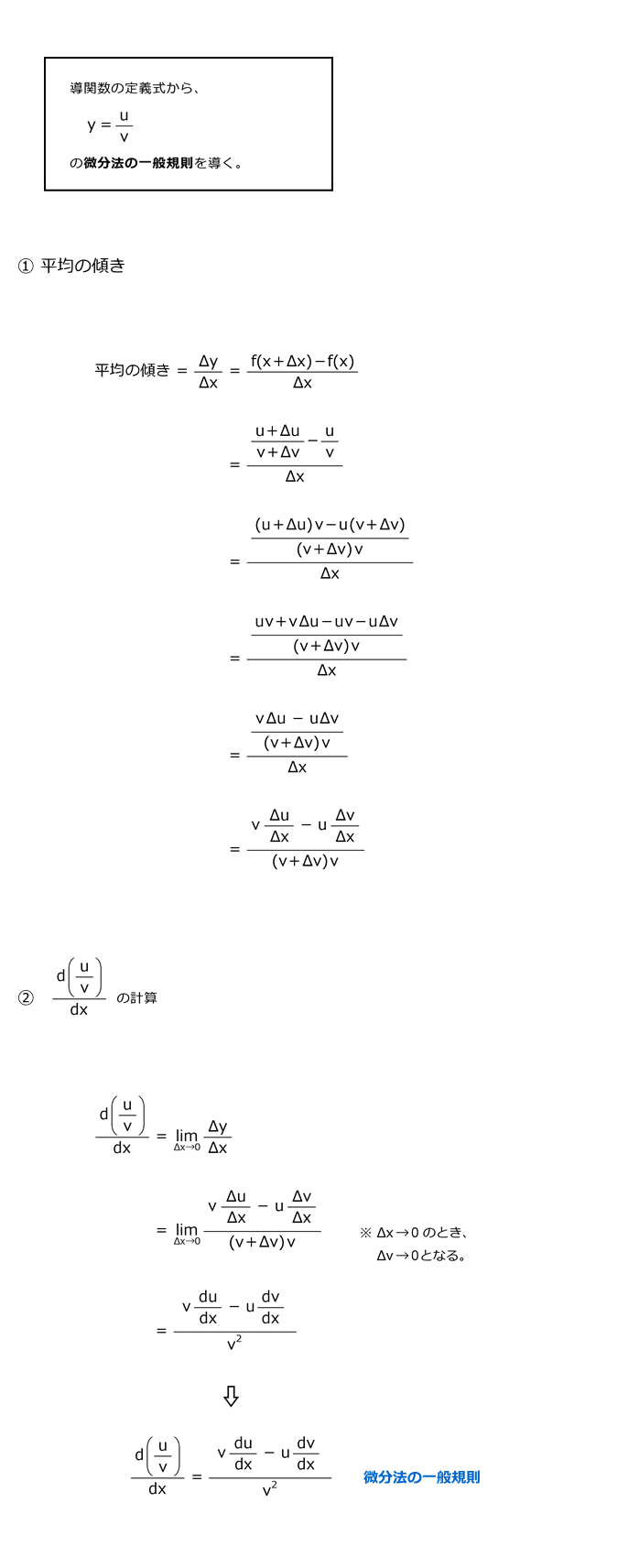
4.5 二つの関数の商の規則
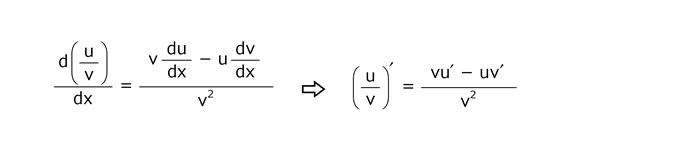
4.6 合成関数の規則

初めての方は、下記の一般規則の導出はサラッと読み進めて、積分までの全体像の把握を再優先にして下さい。
4.7 定数の規則の導出

4.8 定数と関数の積の規則の導出
4.9 二つの関数の和あるいは差の規則の導出
4.10 二つの関数の積の規則の導出
4.11 二つの関数の商の規則の導出
4.12 合成関数の規則の導出

5.微分公式に関する練習問題
この項の目標は、微分公式の活用に慣れることです。
微分積分学公式一覧PDF及び三角関数公式一覧PDFを参照しながらでも構わないので、単に解答を読むだけでなく、手を動かして計算して見て下さい。
置換積分、部分分数分解による積分法、部分積分法を深く理解するために必要不可欠な過程になります。


※一覧PDFをご希望の方は、お問い合わせフォームより連絡下さい。
問題.次の問1~29に示す関数の導関数を求めよ。
問1

解答を表示する

解答を非表示にする
問2
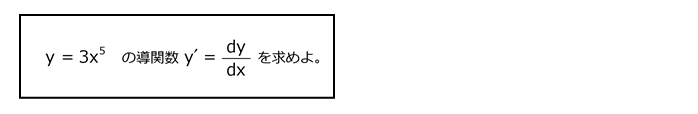
解答を表示する

解答を非表示にする
問3

解答を表示する

解答を非表示にする
問4

解答を表示する

解答を非表示にする
問5

解答を表示する

解答を非表示にする
問6

解答を表示する

解答を非表示にする
問7

解答を表示する

解答を非表示にする
問8

解答を表示する

解答を非表示にする
問9

解答を表示する

解答を非表示にする
問10

解答を表示する
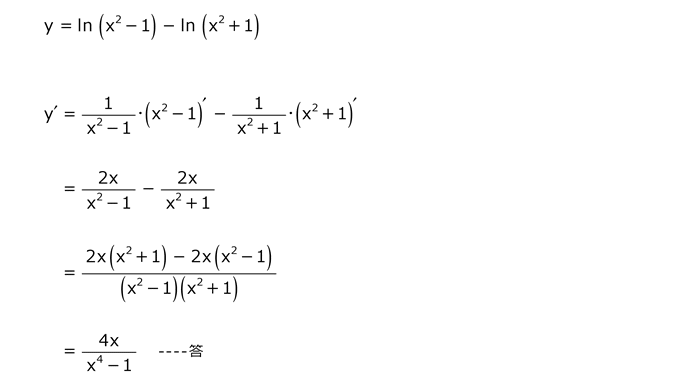
解答を非表示にする
問11
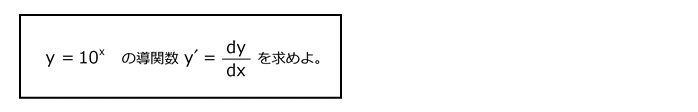
解答を表示する
![]()
解答を非表示にする
問12

解答を表示する

解答を非表示にする
問13
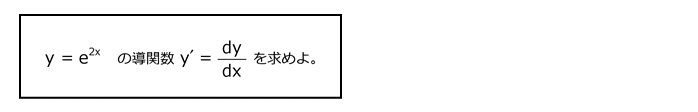
解答を表示する

解答を非表示にする
問14

解答を表示する

解答を非表示にする
問15

解答を表示する

解答を非表示にする
問16

解答を表示する

解答を非表示にする
問17

解答を表示する

解答を非表示にする
問18

解答を表示する

解答を非表示にする
問19

解答を表示する
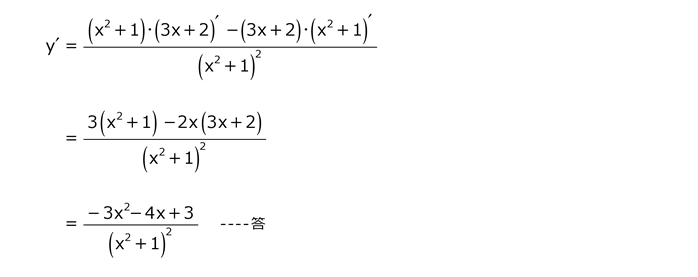
解答を非表示にする
問20

解答を表示する

解答を非表示にする
問21

解答を表示する

解答を非表示にする
問22
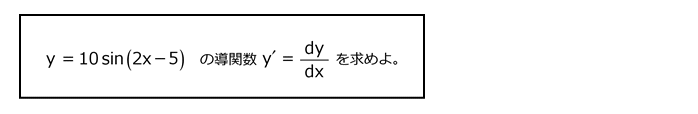
解答を表示する

解答を非表示にする
問23

解答を表示する

解答を非表示にする
問24

解答を表示する
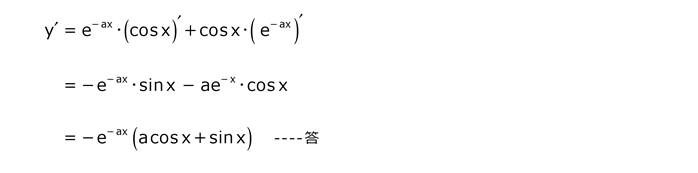
解答を非表示にする
問25

解答を表示する

解答を非表示にする
問26

解答を表示する

解答を非表示にする
問27

解答を表示する

解答を非表示にする
問28

解答を表示する

解答を非表示にする
問29

解答を表示する

解答を非表示にする
6.積分の定義
積分法とは、関数y=f(x)の曲線下の面積についての計算に関するもので、導かれる結果は積分(せきぶん)と呼ばれているものである。
6.1 関数y=f(x)の曲線下の面積ABCD
下記の関数の曲線は、一般的な関数を示すために書いた曲線であり、代表的な関数の曲線に限定されないことを示したものです。
面積ABCDは、灰色の部分の面積のことであり、aとbはx軸の座標を表している。
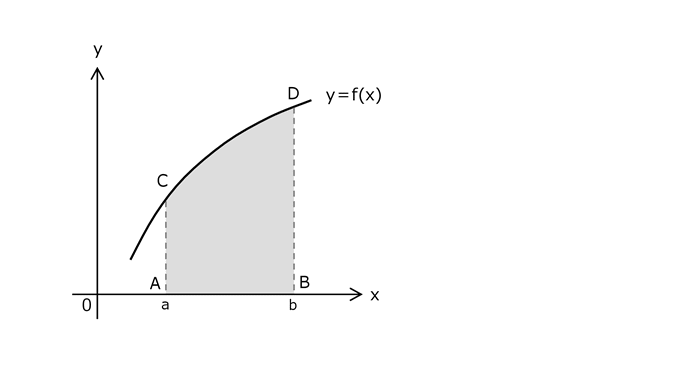
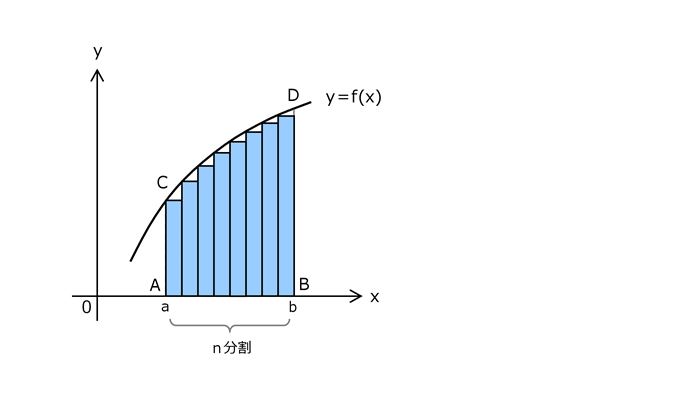
6.2 下部長方形近似
ab間をn分割したときの、
y=f(x)の曲線下の下部長方形近似は、面積ABCDより小さいことがわかる。
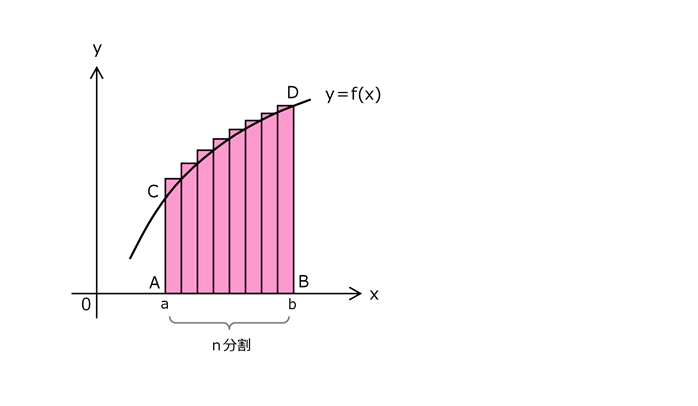
6.3 上部長方形近似
ab間をn分割したときの、
y=f(x)の曲線下の上部長方形近似は、面積ABCDより大きいことがわかる。
6.4 曲線下の面積ABCDの定義
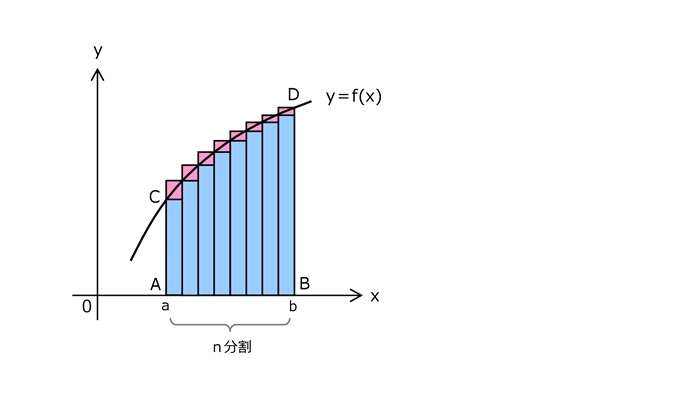
ab間のn分割を限りなく無限大に近づけたときに、下部長方形近似と上部長方形近似が同じ極限値になれば、それを面積ABCDであると定義する。
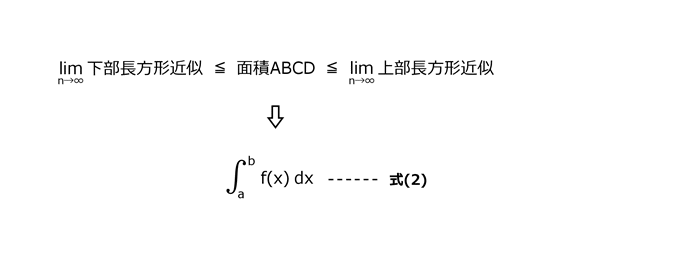
極限値の面積ABCDの表記は、式(2)の記号によって表すことになっている。
この表記を関数y=f(x)のx=aとb間の定積分(ていせきぶん)と呼ぶ。
7.積分公式と不定積分
下記の定積分の定義から、関数y=f(x)の曲線下の面積を求めるのは、大抵の場合困難なことが多い。

式(2)のaを下限値a、bを上限値bという。
7.1 ライプニッツによる定積分の計算方法の発見
定積分の定義から直接計算するのは困難であったが、ドイツの数学者ライプニッツにより、関数g(x)の導関数がf(x)であるとき、つまり、g'(x)=f(x)であれば、式(2)は式(3)の右辺により求めることができるという画期的な方法が発見された。
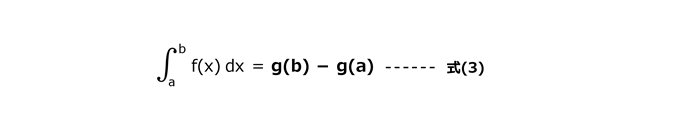
g(b)は、g(x)に上限値であるbを代入したことを示している。
g(a)は、g(x)に下限値であるaを代入したことを示している。
この関数g(x)は、関数f(x)の原始関数又は不定積分(ふていせきぶん)と呼ばれており、式(4)の記号で表記される。
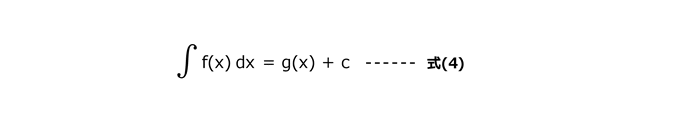
式(4)のCは定数であるが、微分法の一般規則により微分すれば0となるので、式(4)は常に成立する。このCを積分定数という。
関数y=f(x)の不定積分を求めることを積分(せきぶん)と呼んでいる。
積分公式は、以上のことを利用すると簡単にその正否を確認することができる。
7.2 関数y=Xnの積分公式の確認

8.積分公式の一覧
ここでは、積分公式の一覧を下記に示しておきます。
公式の正しさは、右辺を微分することにより簡単に確認することができます。
※各自で確認すること。この程度の確認ができないようでは電験2種に合格はできません。
微分公式の項で、暗記は絶対にダメだといった理由がご理解頂けたでしょうか?
8.1 微分と積分は表裏一体の関係である。
微分と積分は表裏一体の関係です。
微分公式を理解するということは、積分公式を理解することと同義なのです。
下式の流れを理解すれば、微分積分学の主な目的は達成されたも同然です。
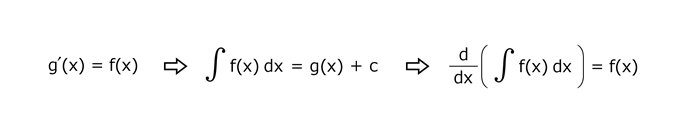
8.2 積分公式の一覧
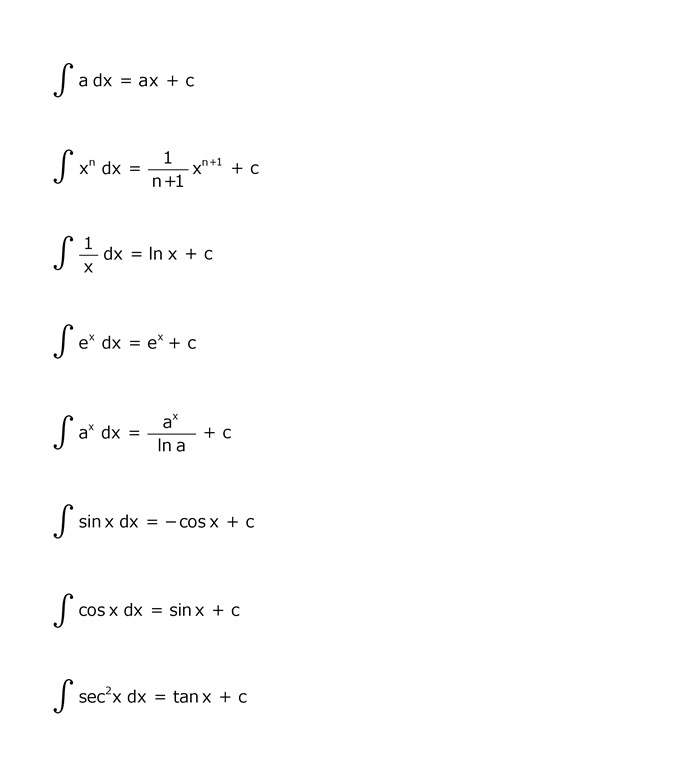
ここでは踏み込みませんが、微分方程式の有用な解を決定するのに、
指数関数y=exの微分と積分の結果は重要な意味を持っています。
「微分しても積分してもexである。」
この単純明快な結果は、塩のような万能調味料を意味します。
つまり、種々の料理(微分方程式)にも合わやすいということです。
微分方程式を学ぶときに必須となるので、必ず覚えておいて下さい。
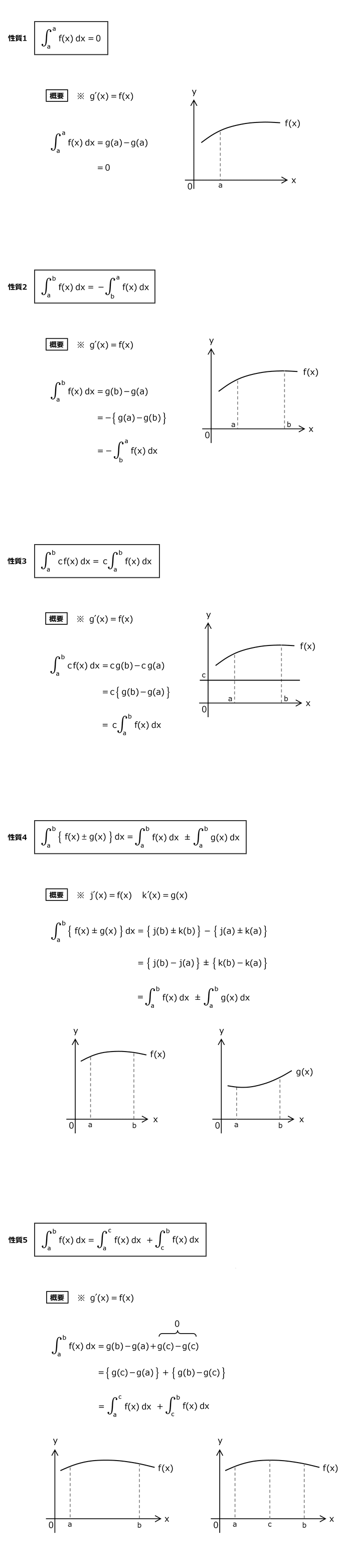
9.定積分の性質
下記の定積分の性質は、種々の関数の面積を計算するときに重要な役割を担います。
直感的に理解できる性質なので確実に覚えましょう。
9.1 定積分の性質の一覧
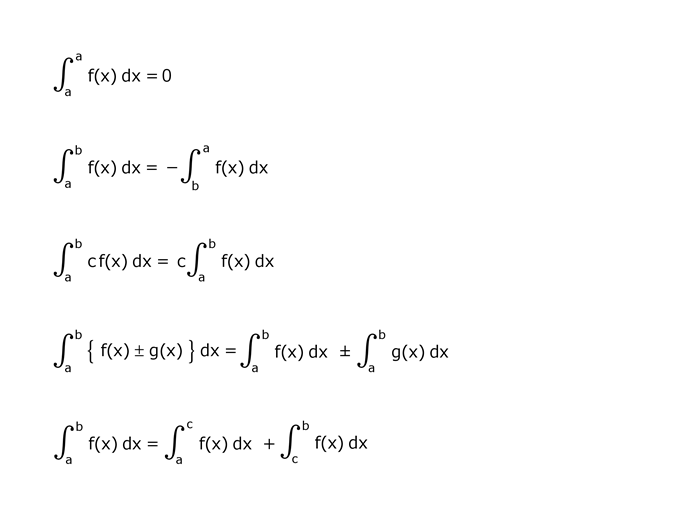
9.2 定績分の性質の概要
不定積分g(x)に、上限値と下限値を代入する前の表記法は、次の二通りがある。
一般的には、①による表記を採用していることが多いが、参考書によっては②の表記で書かれることもあるので、戸惑わないようにすること。
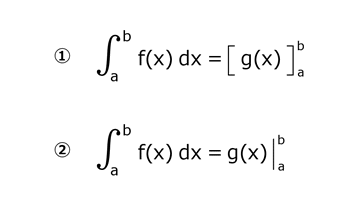
下記の性質1~5の概要では、上記の表記法の過程は省略している。
10.積分公式に関する練習問題
このページの目標は、定積分と不定積分の公式に慣れることです。
微分積分学公式一覧PDF及び三角関数公式一覧PDFを参照しながらでも構わないので、単に解答を読むだけでなく、手を動かして計算して見て下さい。
実際の積分計算は、公式を直接適用できる場面が少なく、特別な工夫による積分法を介して行われます。特別な工夫による積分法とは言っても、最終的には定積分と不定積分の公式を適用することになります。
よって、ここで示す練習問題を軽視することなく、確実に解けるようにして下さい。


問題1.次の問1~13に示す関数の不定積分を求めよ。
問1

解答を表示する

解答を非表示にする
問2

解答を表示する
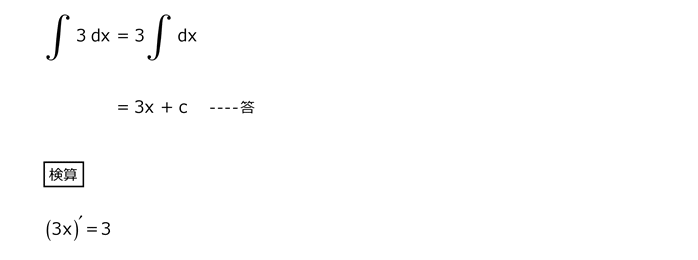
解答を非表示にする
問3

解答を表示する
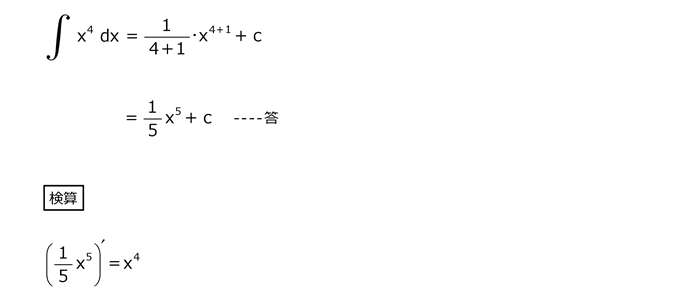
解答を非表示にする
問4

解答を表示する
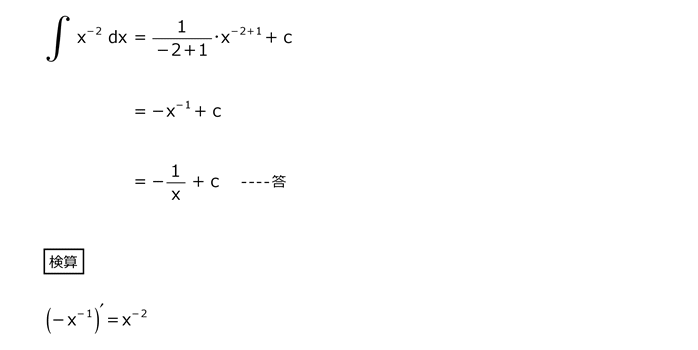
解答を非表示にする
問5

解答を表示する
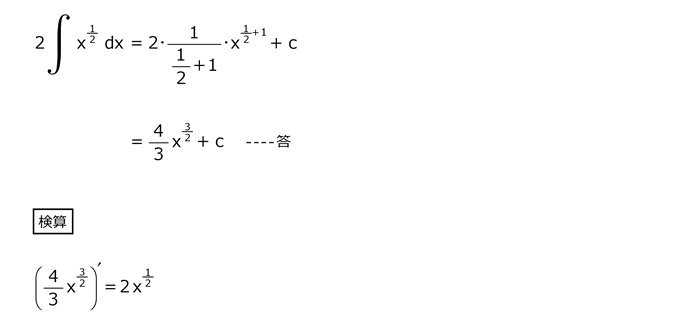
解答を非表示にする
問6

解答を表示する

解答を非表示にする
問7

解答を表示する
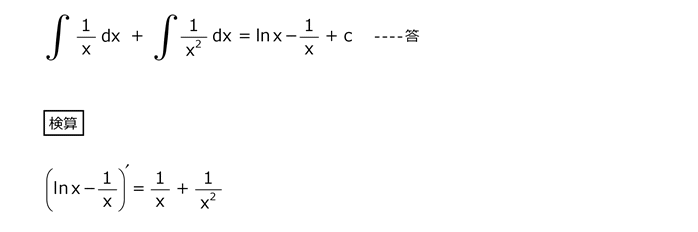
解答を非表示にする
問8

解答を表示する

解答を非表示にする
問9

解答を表示する

解答を非表示にする
問10

解答を表示する

解答を非表示にする
問11

解答を表示する
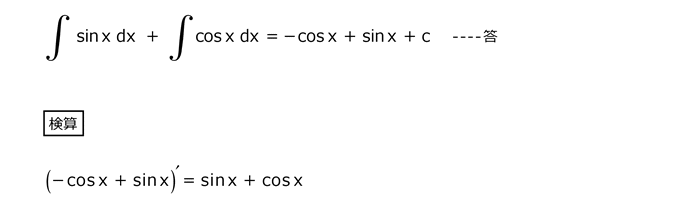
解答を非表示にする
問12

解答を表示する
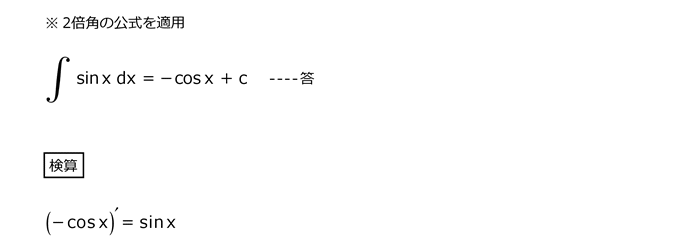
解答を非表示にする
問13

解答を表示する
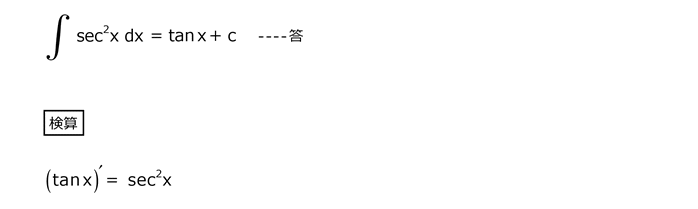
解答を非表示にする
問題2.次の問14~30に示す関数の定積分を求めよ。
問14
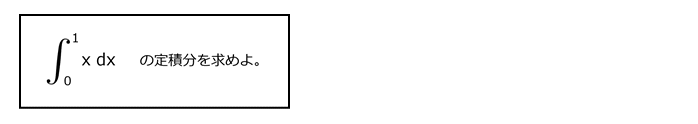
解答を表示する
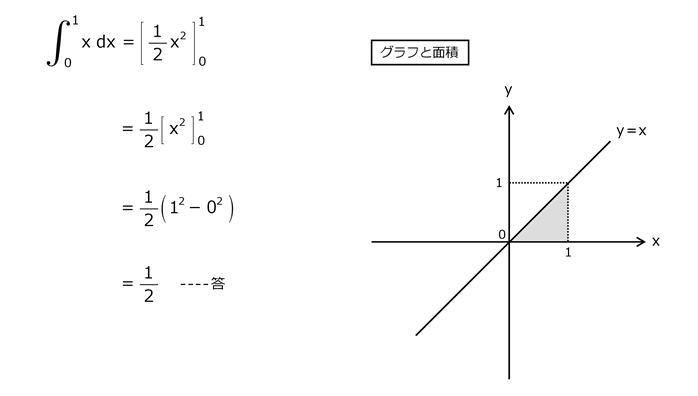
解答を非表示にする
問15
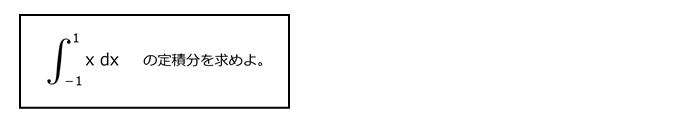
解答を表示する
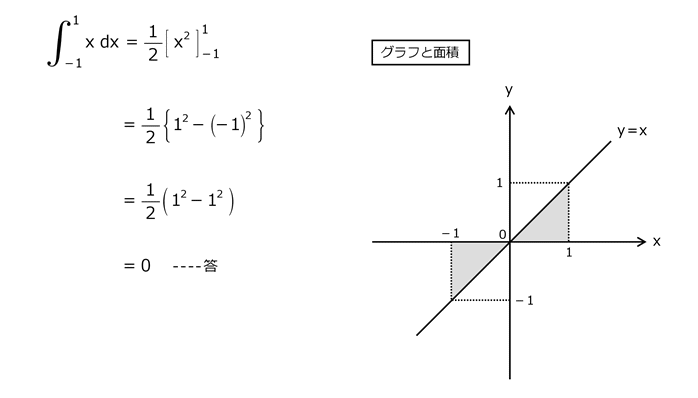
解答を非表示にする
問16

解答を表示する
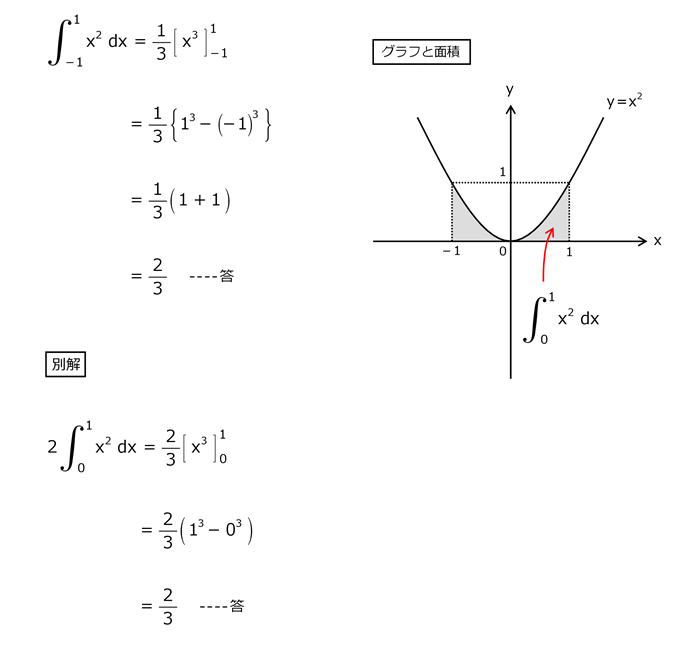
解答を非表示にする
問17

解答を表示する

解答を非表示にする
問18

解答を表示する

解答を非表示にする
問19

解答を表示する
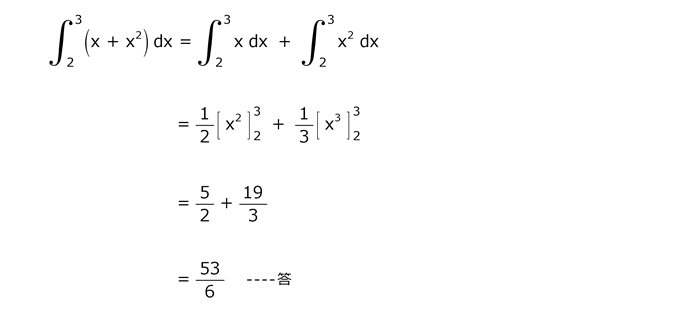
解答を非表示にする
問20

解答を表示する
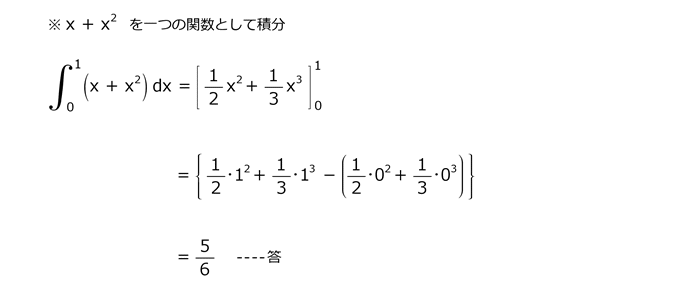
解答を非表示にする
問21

解答を表示する

解答を非表示にする
問22

解答を表示する

解答を非表示にする
問23

解答を表示する
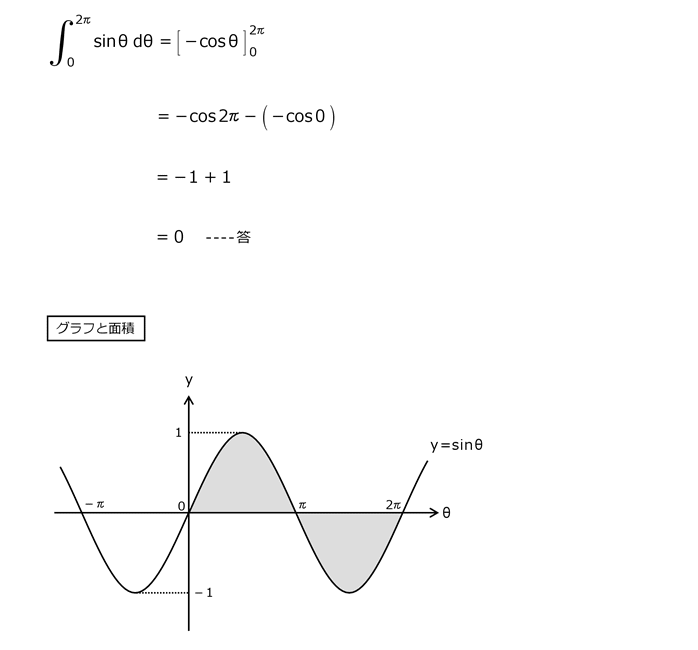
解答を非表示にする
問24

解答を表示する
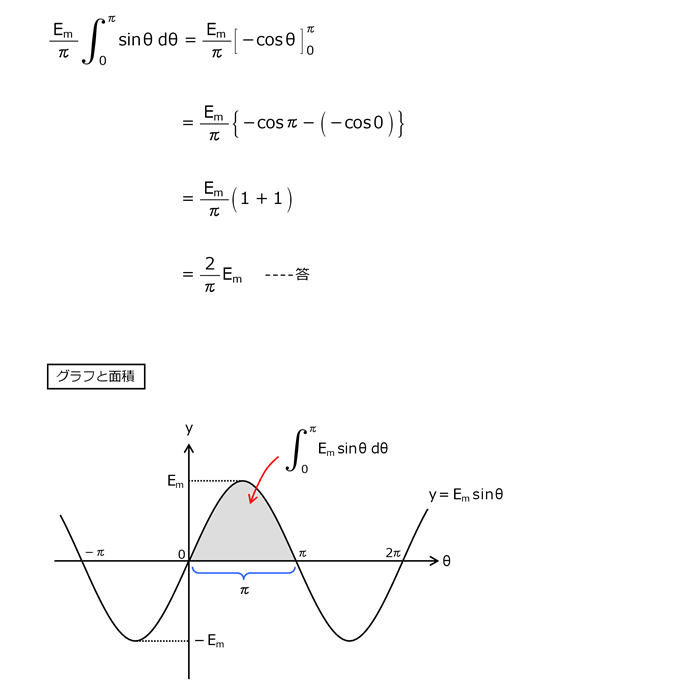
解答を非表示にする
問25

解答を表示する
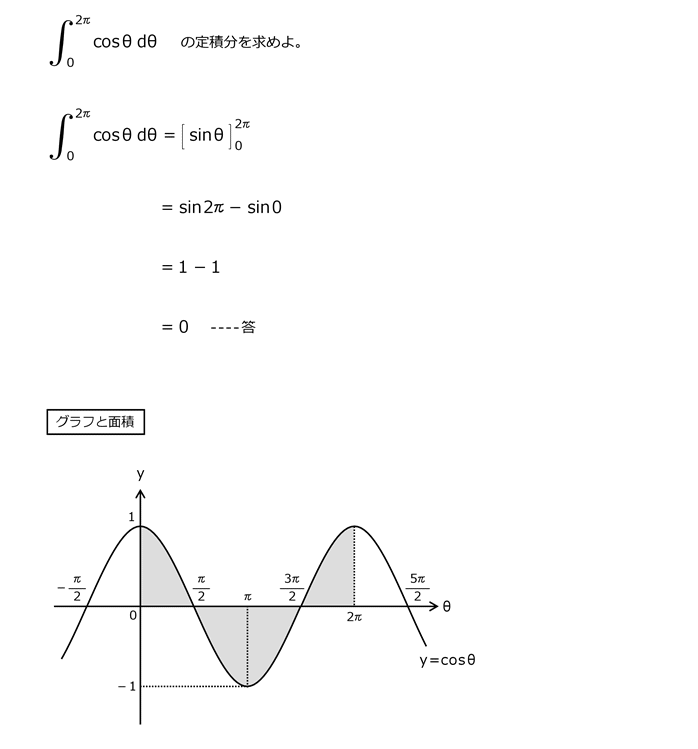
解答を非表示にする
問26

解答を表示する
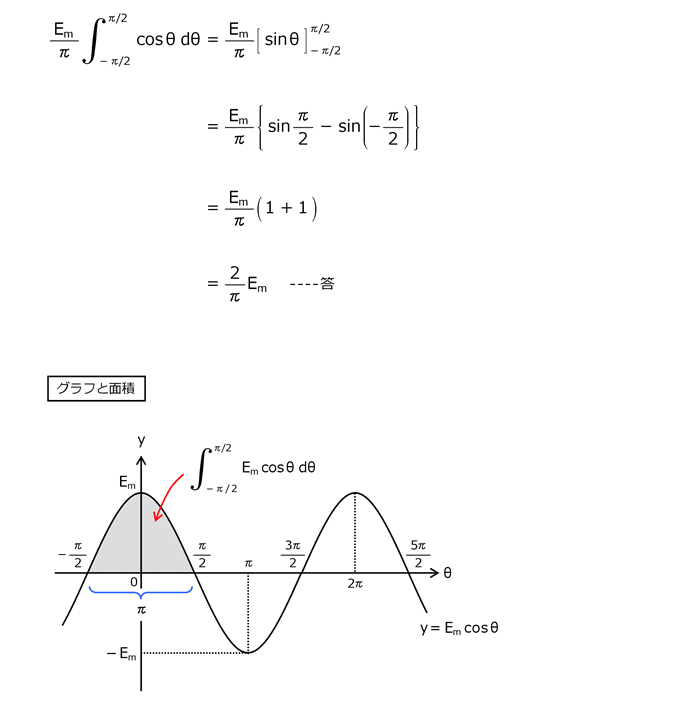
解答を非表示にする
問27

解答を表示する

解答を非表示にする
問28

解答を表示する
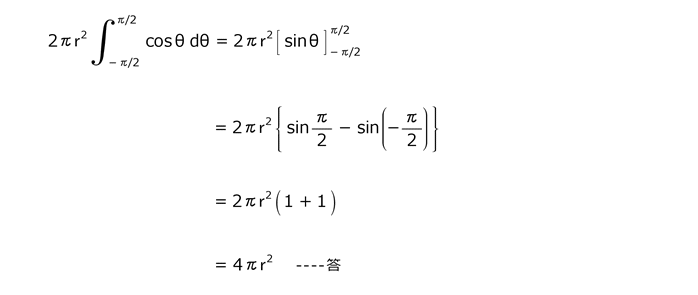
解答を非表示にする
問29

解答を表示する

解答を非表示にする
問30

解答を表示する
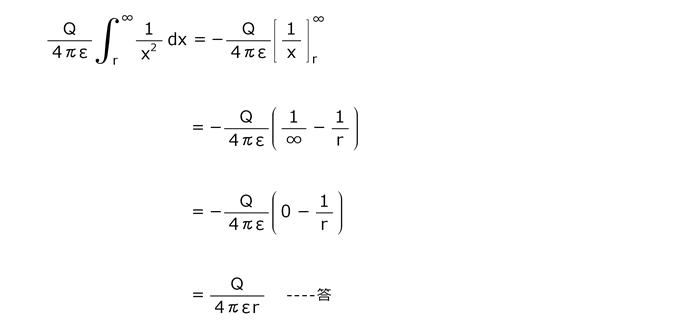
解答を非表示にする






