ブロック線図と等価変換
ブロック線図とは、制御系の信号の流れを視覚的に把握するための図である。
「矢印」「引き出し点」「加え合わせ点」「伝達関数」を制御系のブロック線図を表記に用いる。

1.ブロック線図の図記号
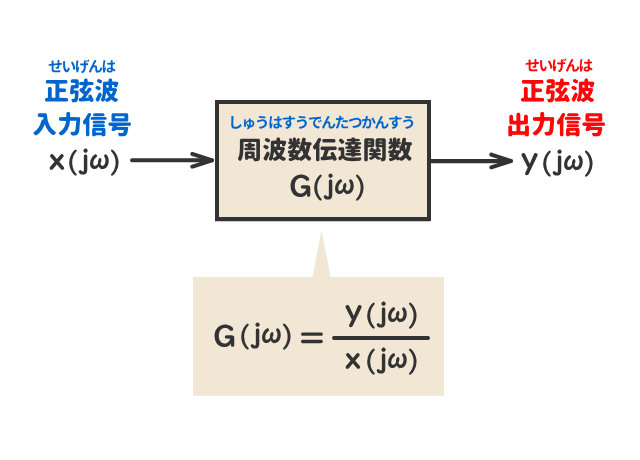
制御系の伝達関数G(s)は、入出力される信号の「伝達要素」を表したものである。
ブロック線図上では「四角形の枠」で囲まれている。
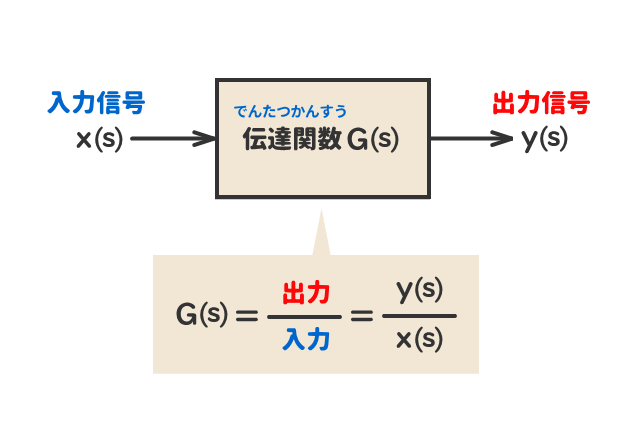
伝達関数G(s)の(s)は信号を意味する。
自明であれば省略しても構わない。
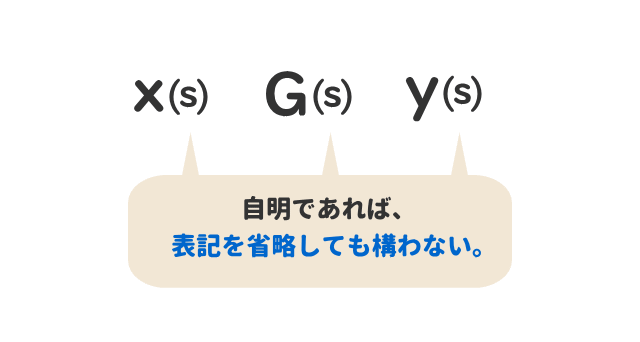
正弦波交流の信号に着目した伝達関数を周波数伝達関数という。
正弦波交流の信号であることを明確に示すために(s)→(jω)と表記する。
自明であれば省略しても構わない。
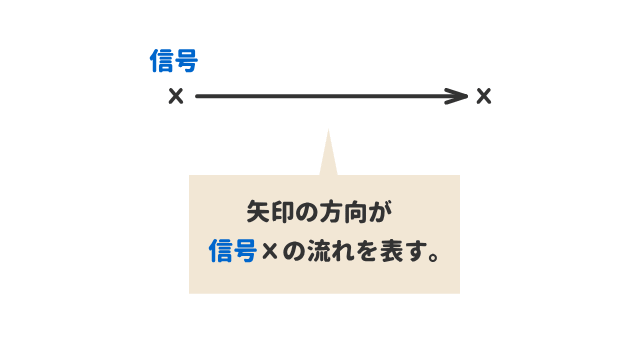
ブロック線図の「信号の流れ」を表す図記号
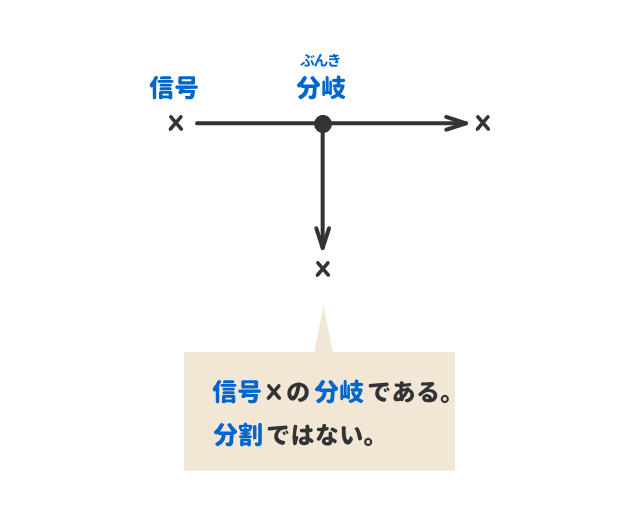
ブロック線図の「信号の分岐」を表す図記号
「引き出し点」
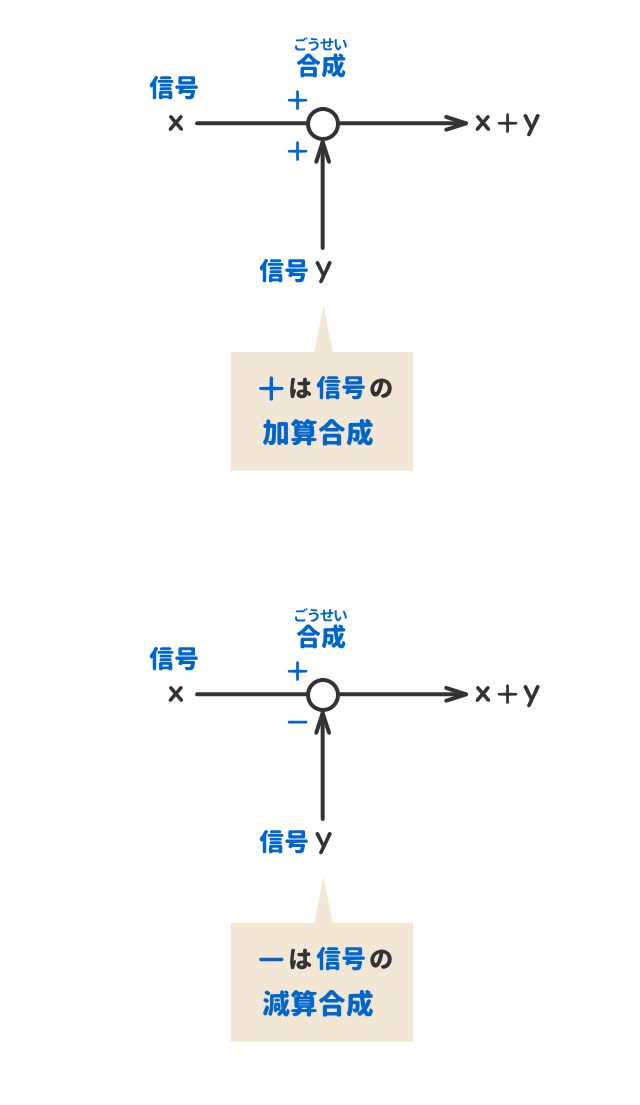
ブロック線図の「信号の合成」を表す図記号
「加え合わせ点」
2.等価とは
等価とは、お互いの価値や働きが同じであることをいう。
二枚の500円玉は、一枚の千円札と同じ価値なので交換することができる。
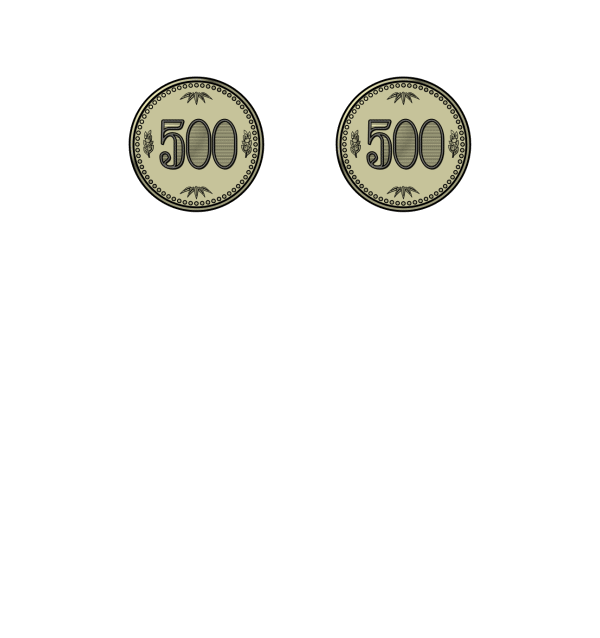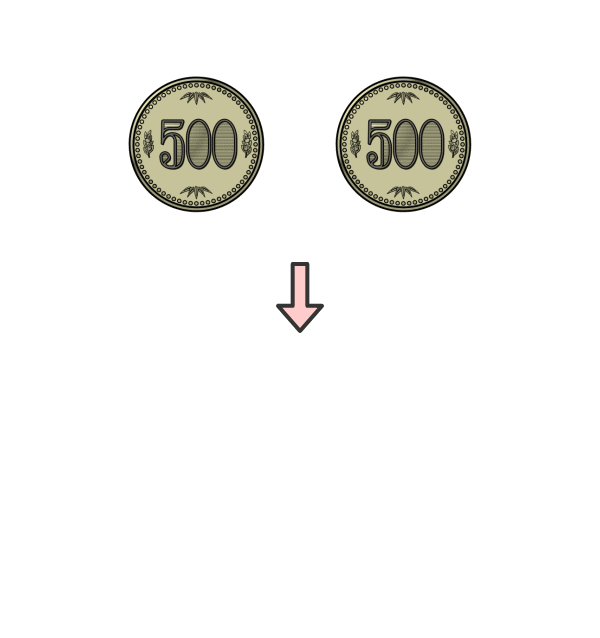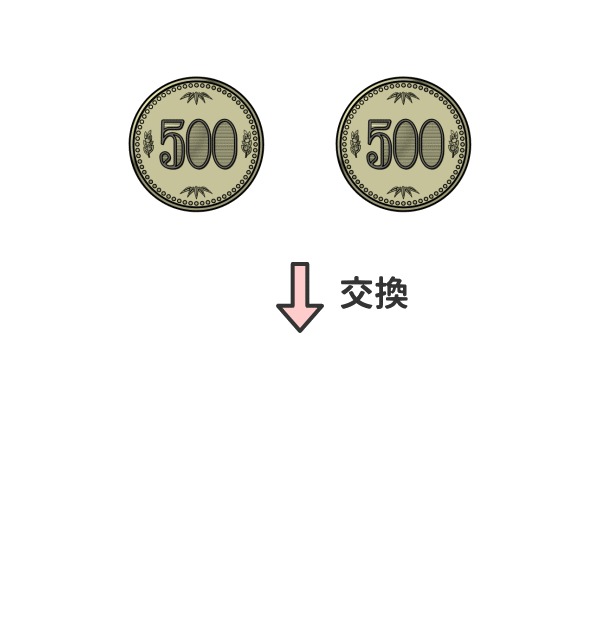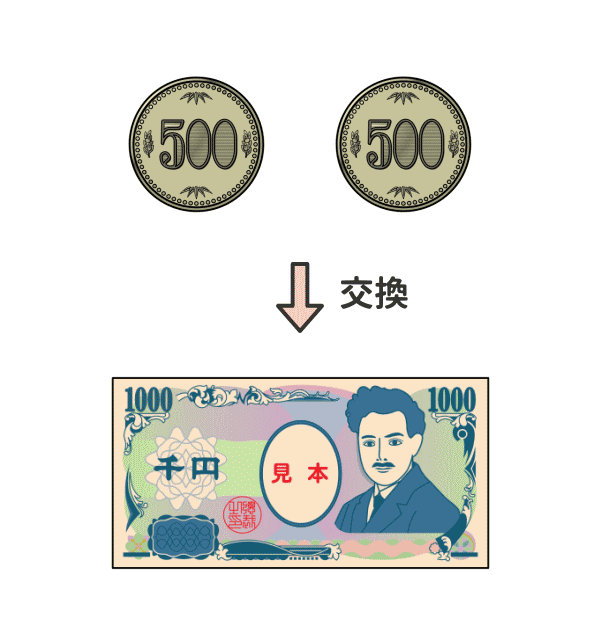
3.ブロック線図の等価変換
ブロック線図が複雑な場合は、解析しやすい形に等価変換する必要がある
「直列結合」「並列結合」「フィードバック結合」「引き出し点の移動」「加え合わせ点の移動」を適用してブロック線図の等価変換を行う。
● 直列結合
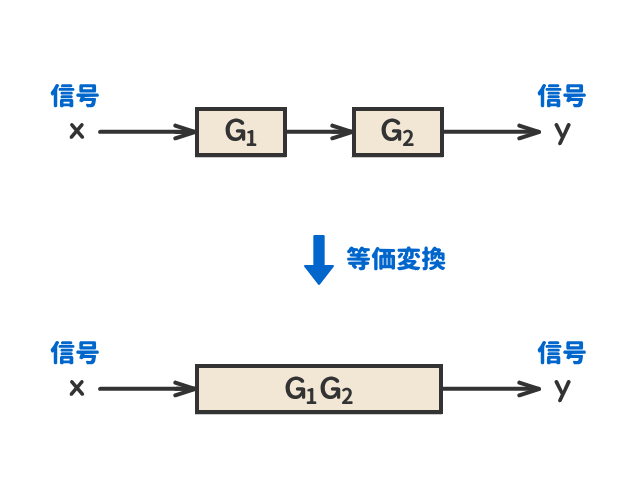
● 並列結合
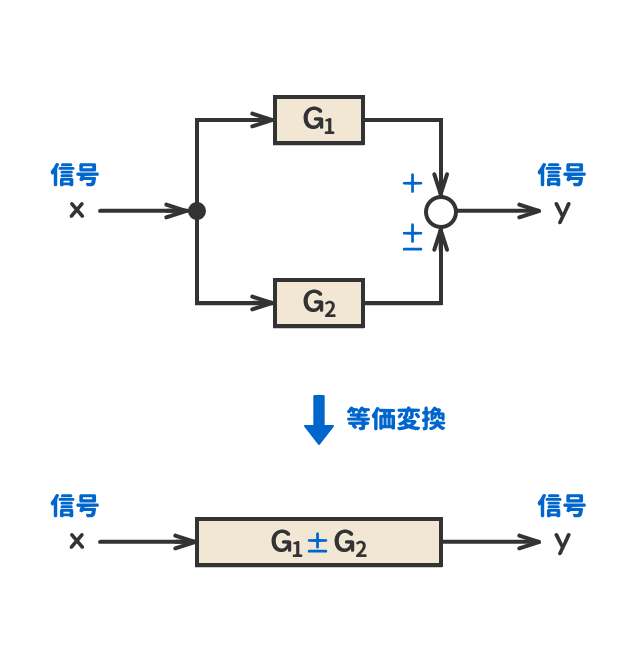
● フィードバック結合
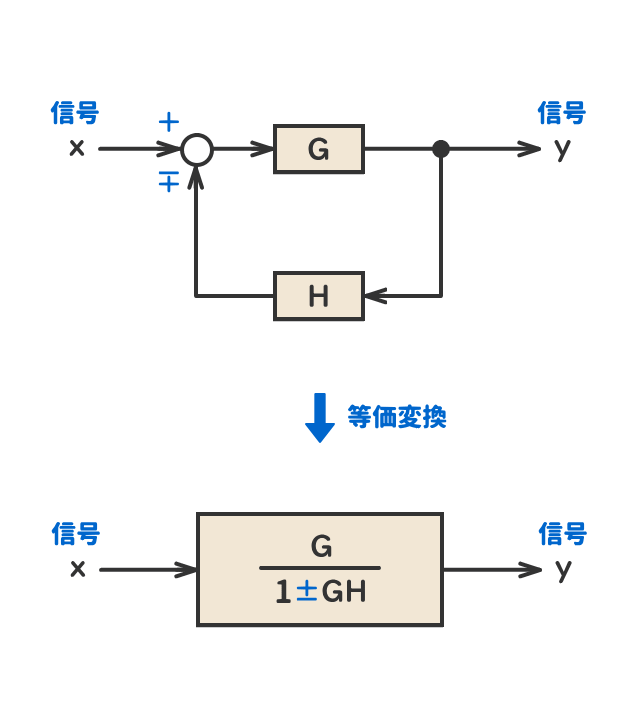
● 引き出し点の移動①
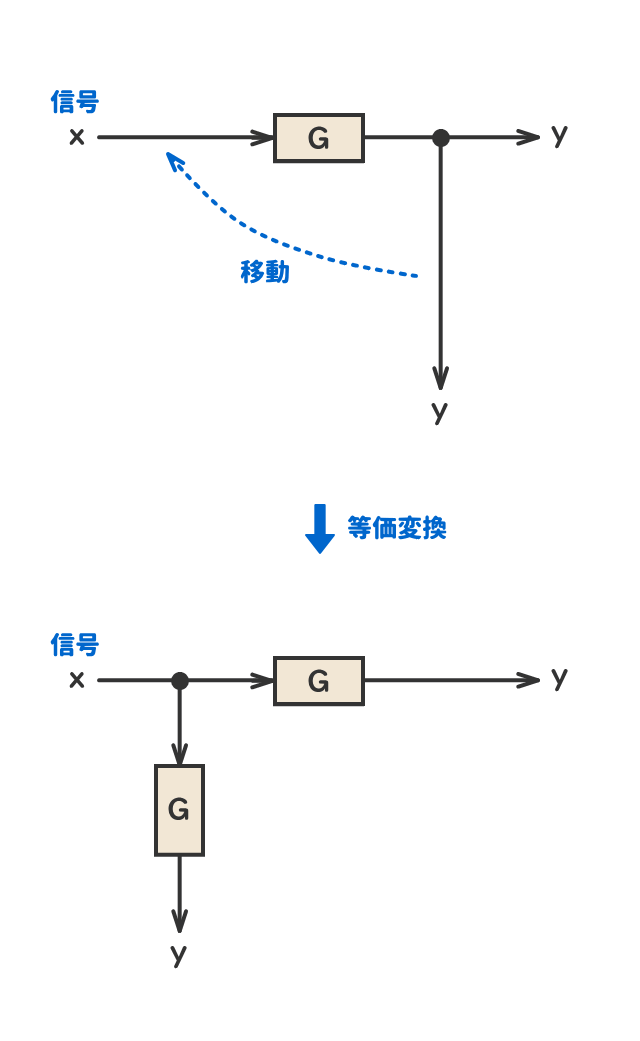
● 引き出し点の移動②
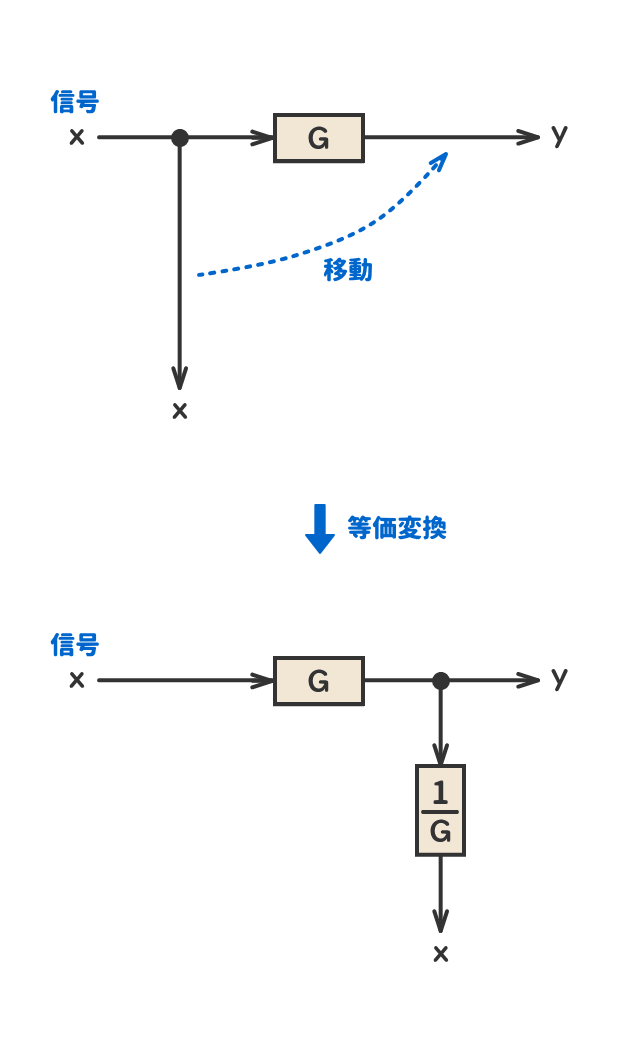
● 加え合わせ点の移動①
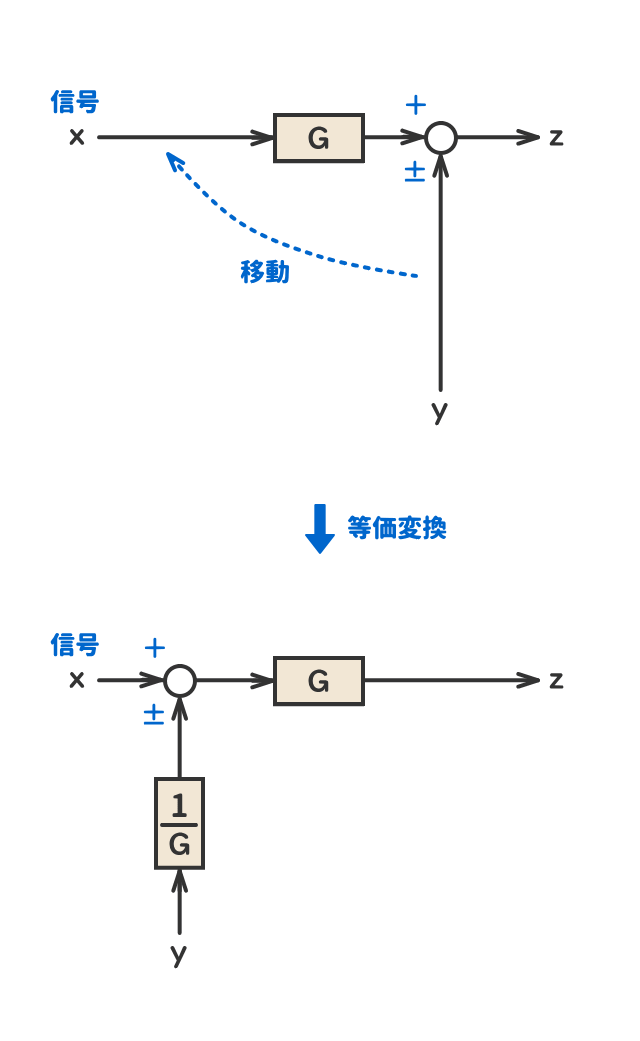
● 加え合わせ点の移動②
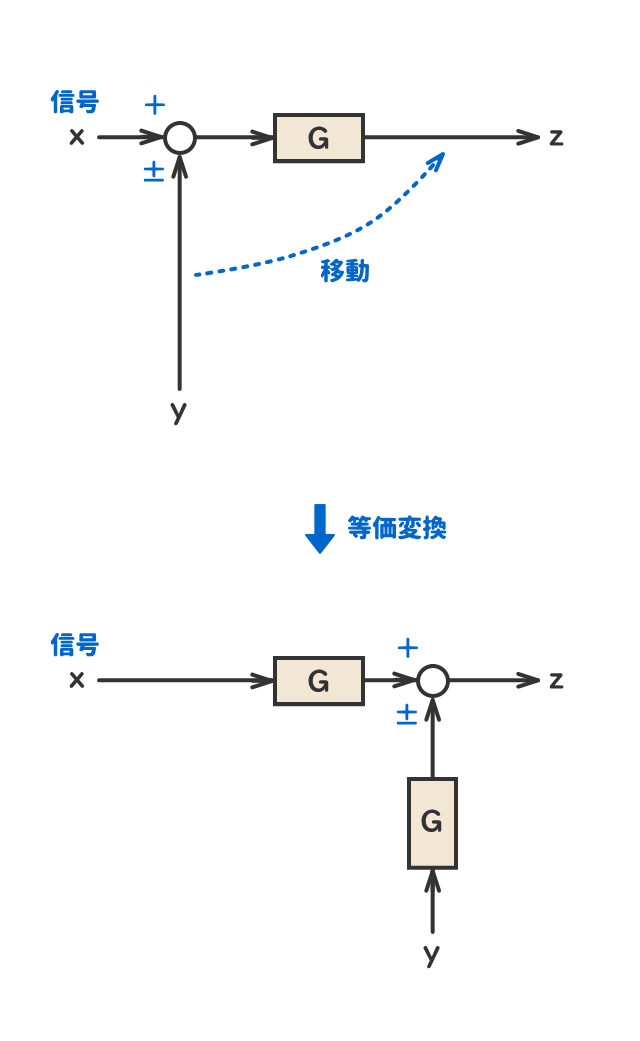
4.等価変換の確認
● 直列結合
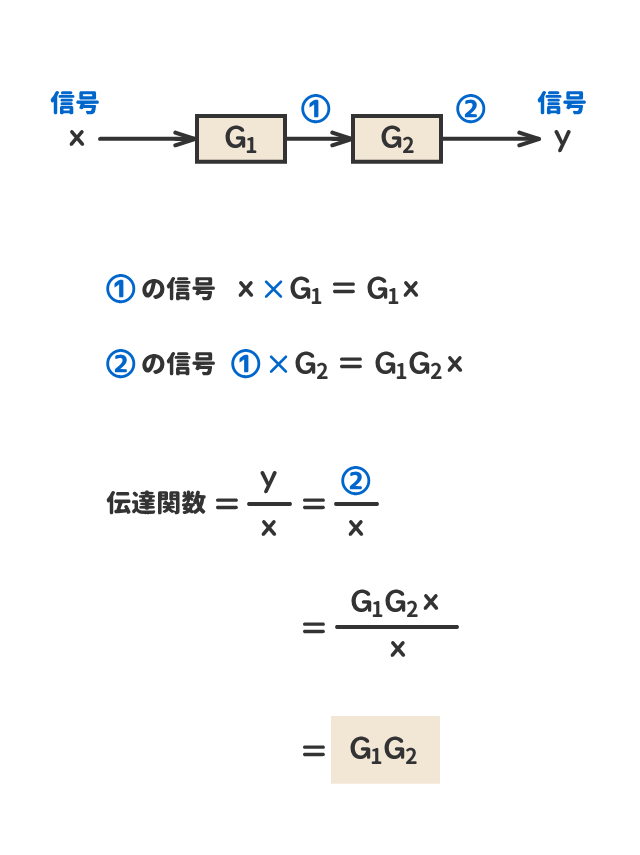
● 並列結合
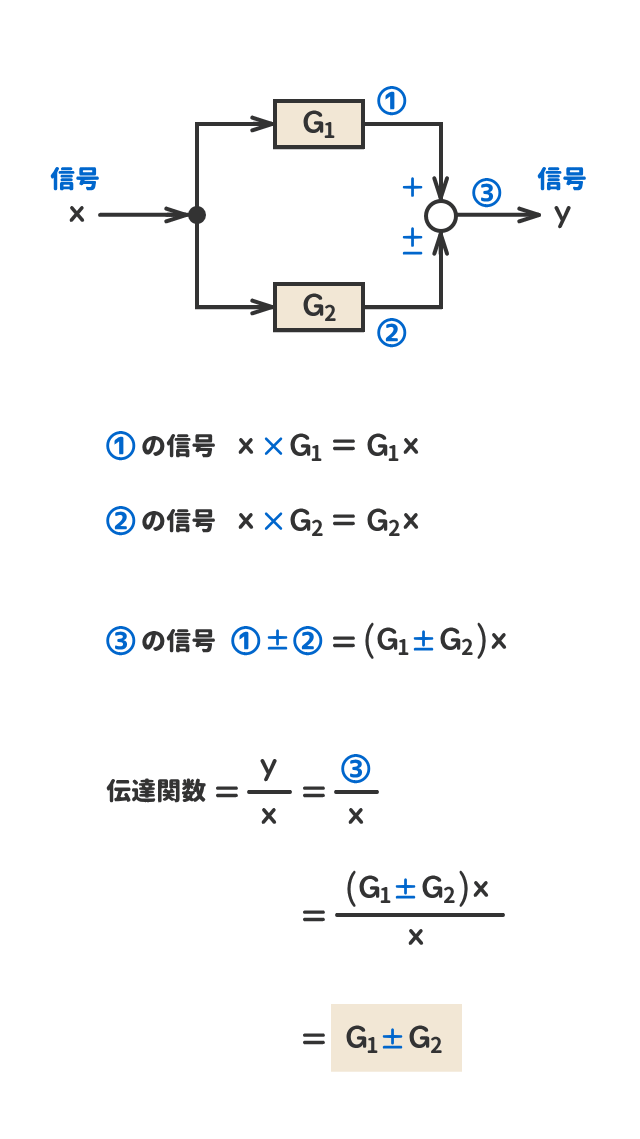
● フィードバック結合
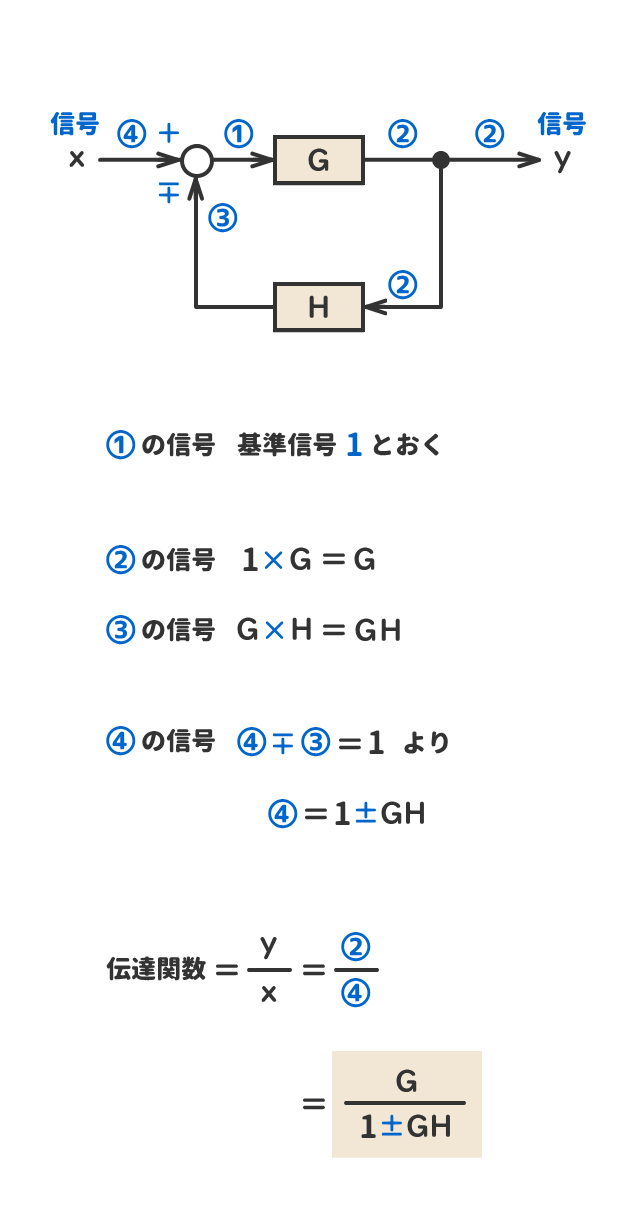
● 引き出し点の移動①
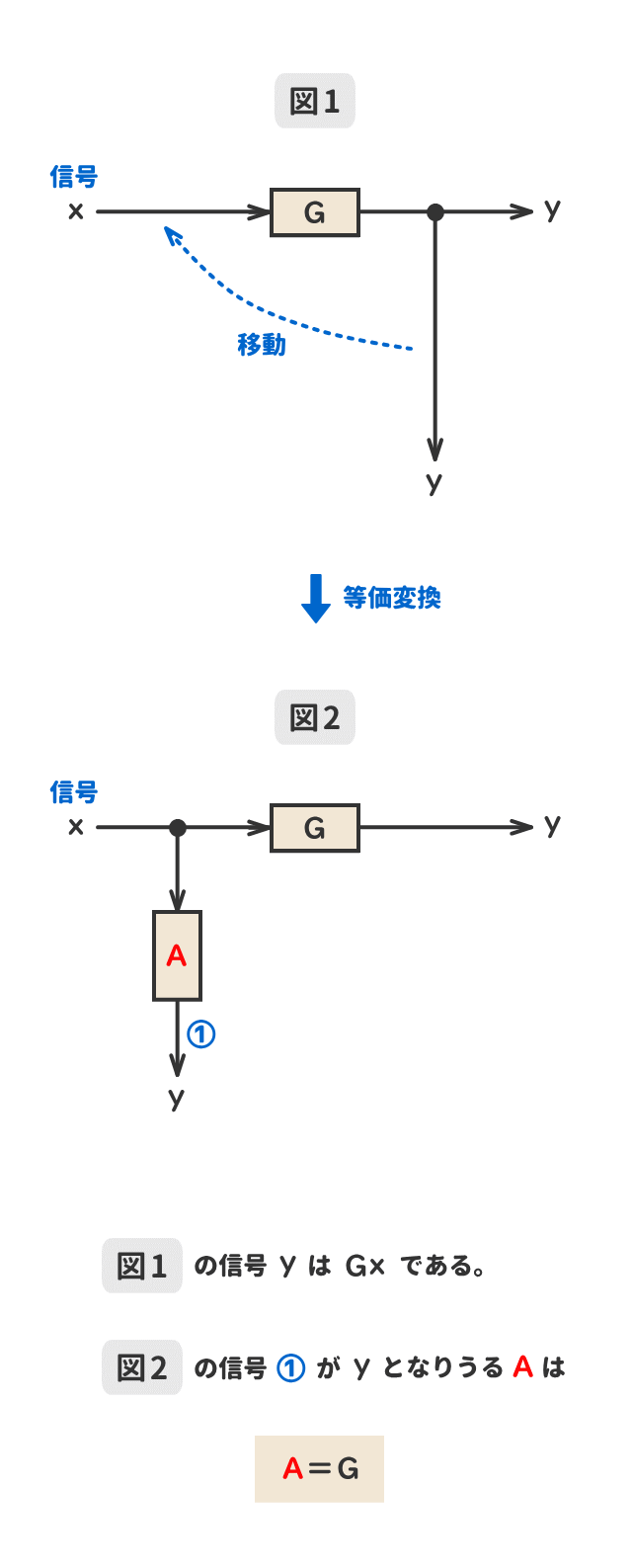
● 引き出し点の移動②
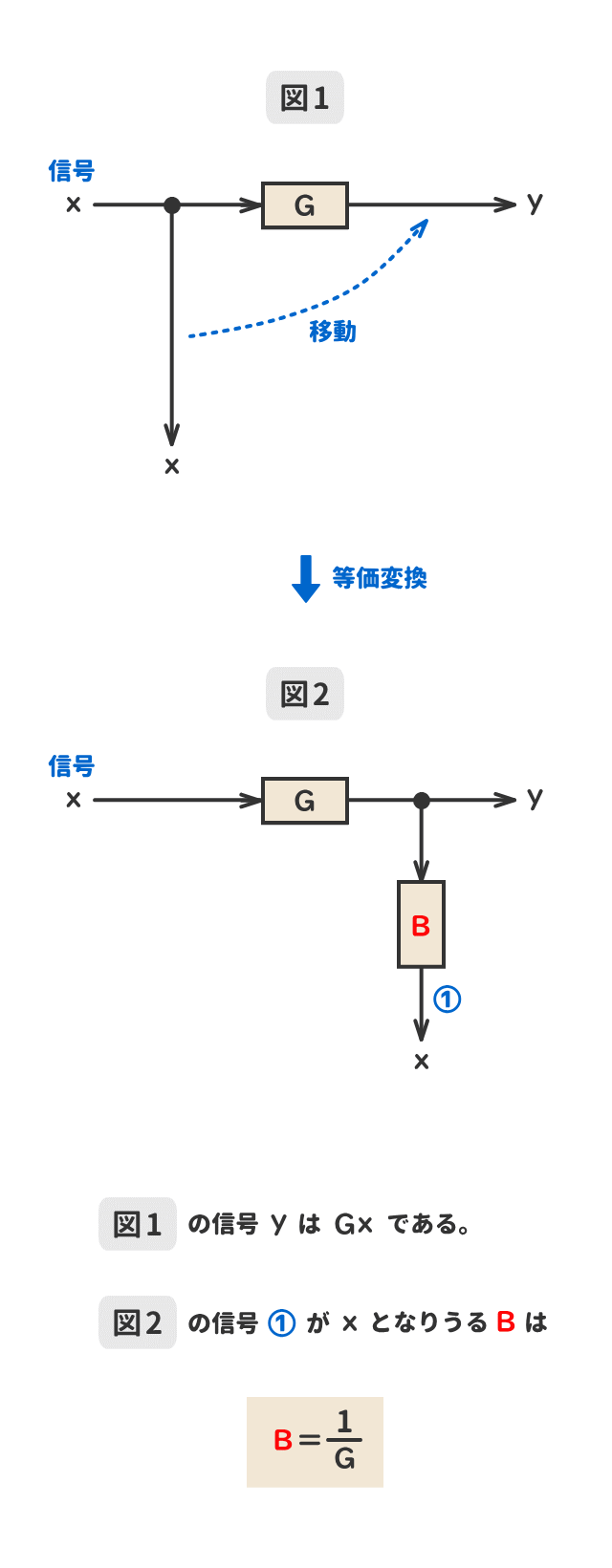
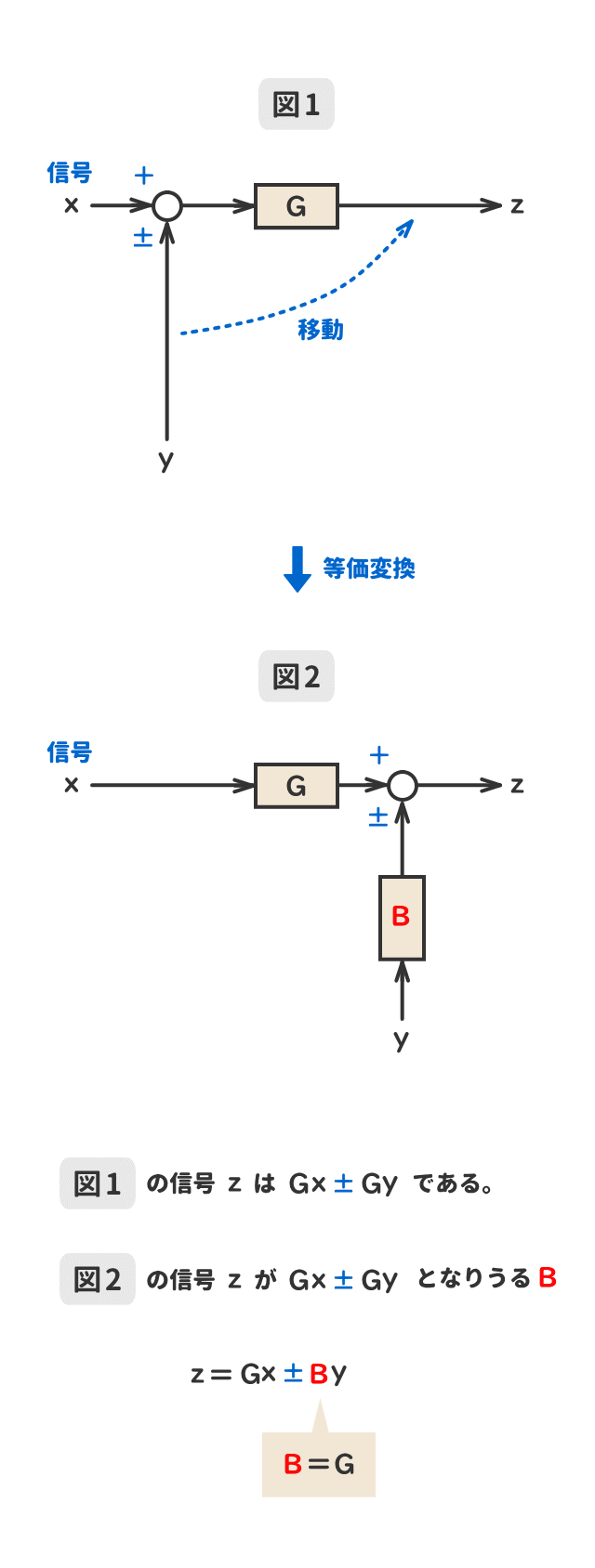
● 加え合わせ点の移動①
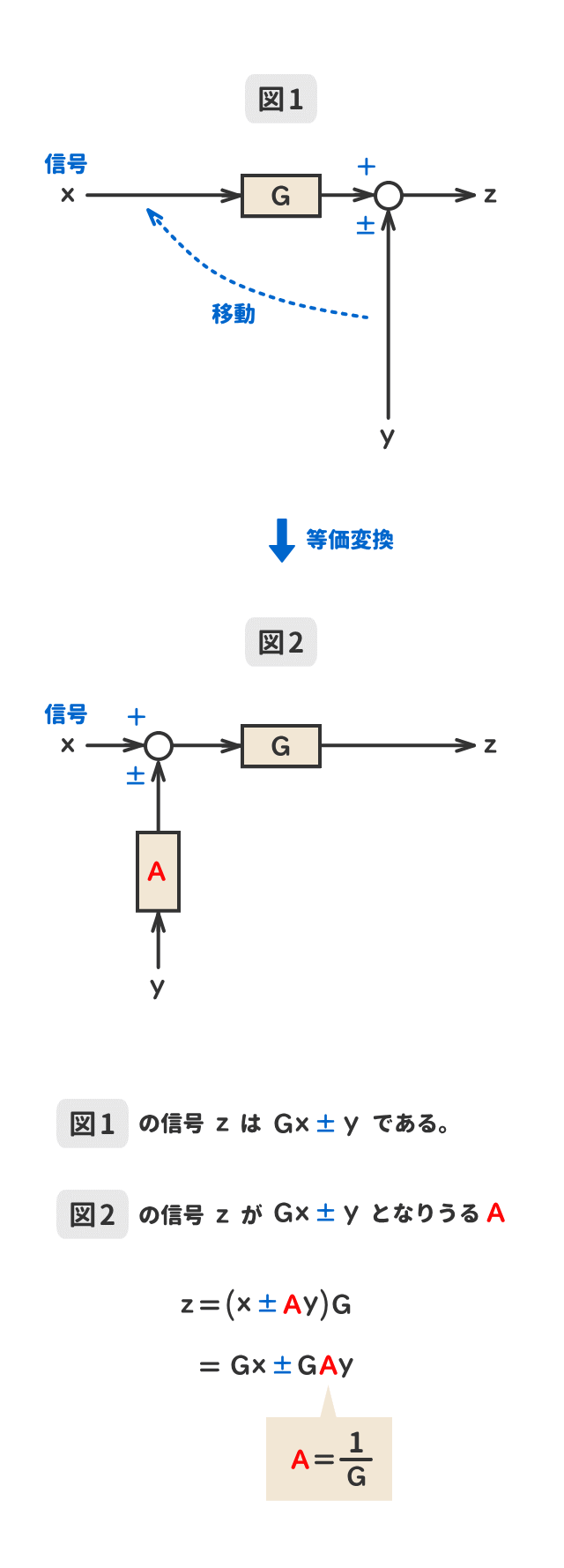
● 加え合わせ点の移動②
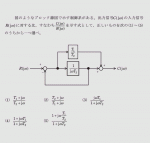
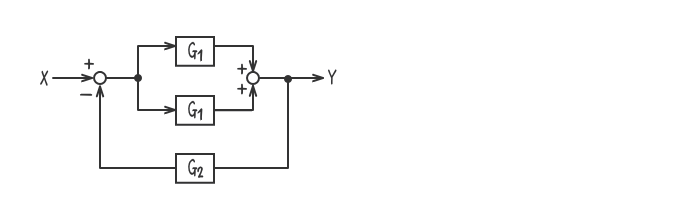
例題1
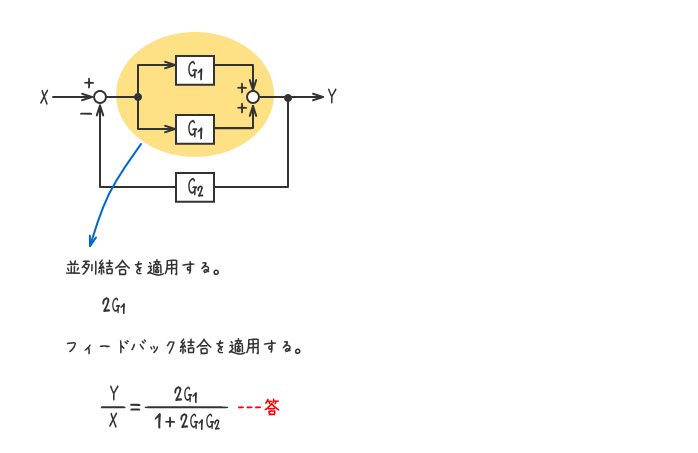
下図のブロック線図の伝達関数(Y/X)を求めよ。
〔臨床工学技士/平成27年度/午後問62一部改定〕
解答を表示する
解答を非表示にする
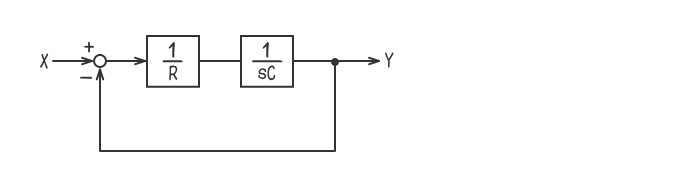
例題2
下図のブロック線図の伝達関数(Y/X)を求めよ。
〔臨床工学技士/平成25年度/午後問63一部改定〕
解答を表示する
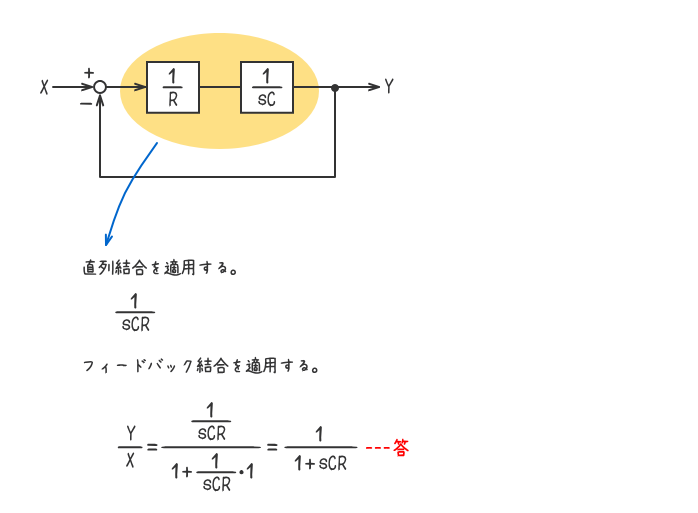
解答を非表示にする
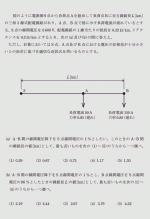
例題3
下図のRL回路の入力信号Ei(jω)と出力E0(jω)の周波数伝達関数G(jω)を時定数T=L/Rの記号を用いて表しなさい。
〔電験3種/平成4年度/電気応用問19改定〕

解答を表示する

解答を非表示にする
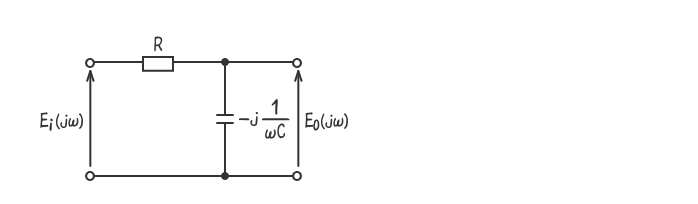
例題4
下図のRC回路の入力信号Ei(jω)と出力E0(jω)の周波数伝達関数G(jω)を時定数T=CRの記号を用いて表しなさい。
〔電験3種/平成5年度/電気応用問20改定〕
解答を表示する
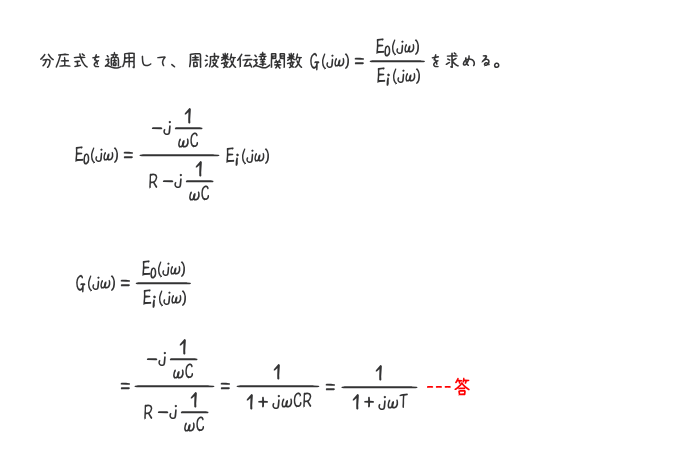
解答を非表示にする
例題5
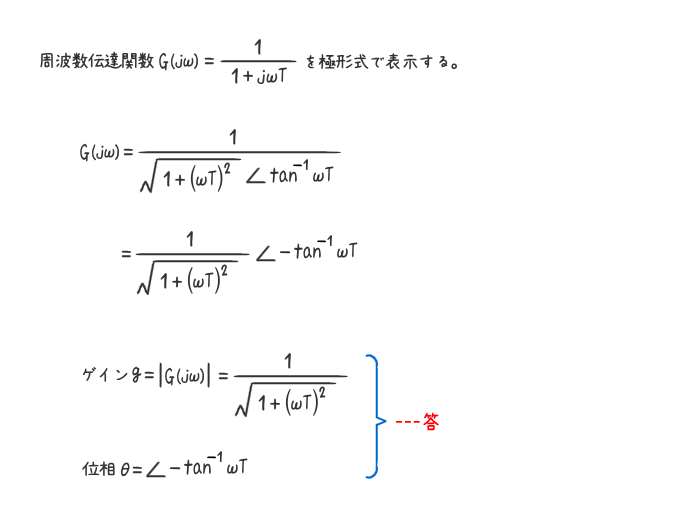
例題3と4の結果で得られた周波数伝達関数G(jω)=1/(1+jωT)の式から、周波数伝達関数のゲインg=|G(jω)|と位相θ=∠G(jω)を求めよ。
解答を表示する
解答を非表示にする
例題6
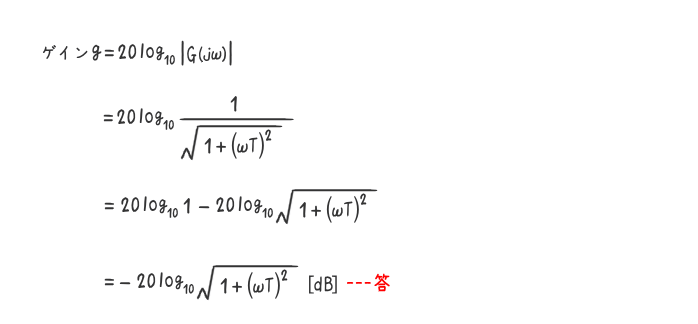
例題5の結果であるゲインg=|G(jω)|のデシベル値g=20log10|G(jω)|を求めよ。
解答を表示する
解答を非表示にする